Практическая работа № 3. Типовые звенья

2015-11-27

889

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Типовые звенья. Дифференциальные уравнения, передаточные функции, временные и частотные характеристики звеньев.

Цель работы: Построение временных и частотных характеристик звеньев

Задание №1: Для расчета и построения переходного процесса при ступенчатом возмущении на входе операторным методом выполнить следующие этапы:

- по заданию построить структурную схему разомкнутой системы;

- определять, передаточную функцию разомкнутой системы и привести её к операторному виду:

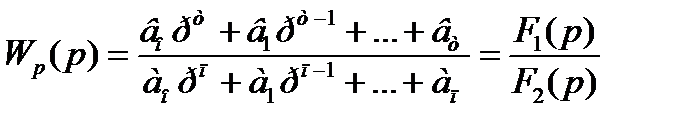(3.1)

- вычислить п корней полинома знаменателя выражения 3.1;

- вычислить производную полинома знаменатели выражения 3.1;

- рассчитать ординаты кривой переходного процесса при нулевых начальных условиях, пользуясь второй теоремой разложения Хевисайда

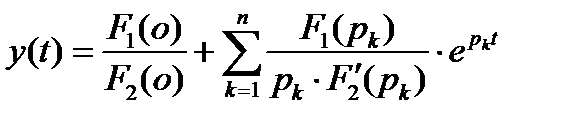(3.2)

где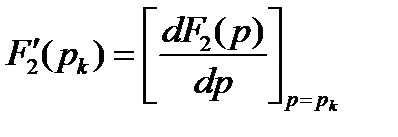

р₁, р₂, …, р_ккорни уравнения 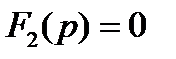при изменении значения времени t дискретно в диапазоне от 0 до 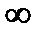. Расчет заканчивается, когда колебания выходной величины становятся достаточно малыми:

- построить переходный процесс, на этот же график нанести заданное значение регулируемой величины, равное вынужденной составляющей переходного процесса ;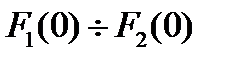

Задача 1 .1

Найти оригиналы по заданным изображениям (табл. 1).

Таблица 1

Задача 1. 2 С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными условиями (табл. 2).

Таблица 2

Задание № 2: Для заданных типовых звеньев требуется построить временные и частотные характеристики. Вид типового звена, его параметры в соответствии с номером варианта приведены в таблице 3.1.

Для построения частотных характеристик (ЧХ) ТДЗ необходимо выполнить следующие этапы:

- написать передаточную функцию (ПФ) исследуемого звена;

- произвести формальную замену, оператора р и 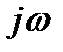и выделить вещественную и мнимую части комплексного коэффициента усиления, которые соответственно дадут аналитические выражения вещественной частотной характеристики (ВЧХ) и мнимей частотной характеристики (МЧХ) - 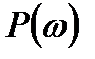и ;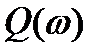

- получить выражению для амплитудно-частотной характеристики звена (АЧХ) - 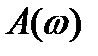по формуле:

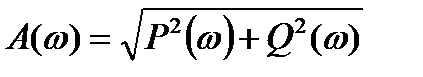
- получить выражение для фазочастотной характеристики звена (ФЧХ) - 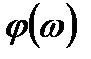по формуле:

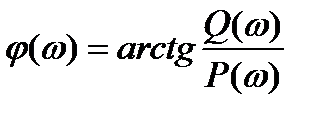
произвольно задаваясь значениями круговой частоты 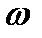в диапазоне от 0 до 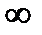вычислить значение ВЧХ, АЧХ, ФЧХ. Выбор фиксированных 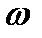произвести таким образом, чтобы полученные значения этих характеристик давали полное представление о форме искомой кривой.

Таблица 3.1 – Исходные данные

№ вар-та	Типовое динамическое звено
вид	параметры
k	T₁, с	T₂, с	x
	Апериодическое 1-го порядка		0,05	-	-
	Апериодическое 2-го порядка				-
	Колебательное			-	0,8
	Интегрирующее с замедлением		0,04	-	-
	Дифференцирующее с замедлением		0,32	-	-
	Апериодическое 1-го порядка		0,1	-	-
	Апериодическое 2-го порядка		0,6	0,2	-
	Колебательное		0,5	-	0,1
	Интегрирующее с замедлением		3,8	-	-
	Дифференцирующее с замедлением		0,02	-	-
	Апериодическое 1-го порядка		0,8	-	-
	Апериодическое 2-го порядка		2,5	0,5	-
	Колебательное		1,5	-	0,6

Продолжение таблицы 3.1

№ вар-та	Типовое динамическое звено
вид	параметры
k	T₁, с	T₂, с	x
	Интегрирующее с замедлением		4,4	-	-
	Дифференцирующее с замедлением		0,7	-	-
	Апериодическое 1-го порядка		0,12	-	-
	Апериодическое 2-го порядка				-
	Колебательное			-	0,2
	Интегрирующее с замедлением		1,25	-	-
	Дифференцирующее с замедлением		0,09	-	-
	Апериодическое 1-го порядка		0,55	-	-
	Апериодическое 2-го порядка		1,2	0,4	-
	Колебательное		2,4	-	0,5
	Интегрирующее с замедлением		0,45	-	-
	Дифференцирующее с замедлением		3,2	-	-
	Апериодическое 1-го порядка		0,15	-	-
	Апериодическое 2-го порядка			0,8	-
	Колебательное		1,6	-	0,3
	Интегрирующее с замедлением		0,28	-	-
	Дифференцирующее с замедлением		0,9	-	-
	Апериодическое 1-го порядка		0,08	-	-
	Апериодическое 2-го порядка		0,4	0,1	-
	Колебательное		1,8	-	0,4
	Интегрирующее с замедлением		5,2	-	-
	Дифференцирующее с замедлением		0,04	-	-
	Апериодическое 1-го порядка		0,4	-	-
	Апериодическое 2-го порядка			0,9	-
	Колебательное			-	0,05
	Интегрирующее с замедлением		1,65	-	-
	Дифференцирующее с замедлением		0,56	-	-
	Апериодическое 1-го порядка		0,02	-	-
	Апериодическое 2-го порядка			0,6	-
	Колебательное			-
	Интегрирующее с замедлением		0,16	-	-
	Дифференцирующее с замедлением		0,01	-	-
	Апериодическое 1-го порядка		0,6	-	-
	Апериодическое 2-го порядка			0,3	-
	Колебательное		3,4	-	0,6
	Интегрирующее с замедлением		1,98	-	-
	Дифференцирующее с замедлением		2,4	-	-

Теоретическая часть

2015-11-27

889

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Обсуждение в статье: Практическая работа № 3. Типовые звенья

Обсуждений еще не было, будьте первым... ↓↓↓