Формы записи дифференциальных уравнений

 

Стационарные линейные непрерывные САУ наиболее часто описываются линейными дифференциальными уравнениями с постоянными коэффициентами:

 

. (2.9)

 

 

В этом уравнении - выходная переменная (управляемая (регулируемая) величина) САУ, - входная переменная САУ. Правая часть уравнения (3.1) записана относительно управляющего воздействия , однако используются формы записи уравнения относительно задающего воздействия , возмущения или нескольких входных воздействий.

Применяется также операторная форма записи уравнения (2.9):

 

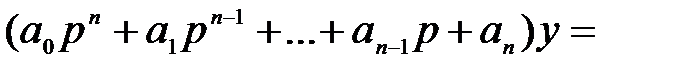
. (2.10)

 

В этом уравнении через « » обозначен оператор дифференцирования .

Заметим, что по сложившейся традиции символ « » используется также в преобразованиях Лапласа и Карсона-Хевисайда, но является комплексным числом .

За многолетнюю историю развития ТАУ сложились традиции формальной записи линейных дифференциальных уравнений, описывающих стационарные САУ. В учебной литературе по ТАУ они рассматриваются как стандартные формы записи дифференциальных уравнений. Рассмотрим эти формы записи на примере линейной системы второго порядка:

 

(2.11)

 

или в операторной форме

 

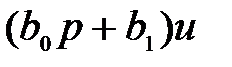. (2.12)

 

Первая стандартная символическая форма записи уравнения (2.11) имеет следующий вид:

, (2.13)

 

где ; ; ; .

Форма (2.13) представляет собой операторно-структурное описание системы, т.е. в виде операторов звеньев, составляющих структурную схему системы (далее эти понятия разъясняются), и связей между ними. В этой форме - постоянные времени звена, измеряемые в секундах; - передаточный коэффициент звена.

Из изложенного выше следует, что уравнение (2.9) в этой форме перепишется в следующем виде:

 

, (2.14)

 

где ; ; .

 

Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы, которая для рассматриваемого примера (2.11) имеет вид

 

.

 

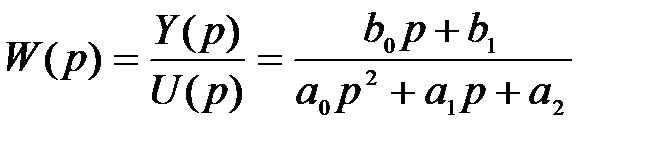Передаточная функция САУ, поведение которой во времени описывается уравнением (2.9), имеет следующий вид :

 

.

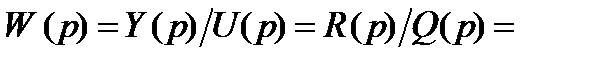
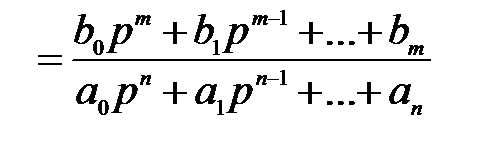(2.15)

В формуле (2.15) через 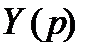и обозначены изображения (по Лапласу) выходной и входной переменных САУ при нулевых начальных условиях и равенстве нулю внешних возмущений, а через и - полиномы относительно комплексной переменной .

Вторая стандартная форма записи дифференциального уравнения имеет следующий вид:

или 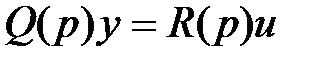. (2.16)

 

В (2.16) и являются полиномами (символическими) относительно оператора .

Из сравнения первой и второй стандартных форм записи дифференциальных уравнений следует, что с математической точки зрения различие между этими формами весьма несущественно и состоит лишь в различном представлении коэффициентов уравнений. В ТАУ принято называть уравнения вида (2.9) - (2.14), (2.16) уравнениями типа «вход-выход».

Третья стандартная форма записи дифференциального уравнения принципиально отличается от форм записи, описанных выше. В этой форме записи используются переменные состояния. Отметим, что понятие «состояние» является базовым в современной ТАУ (СТАУ). Переменные состояния - это промежуточные переменные системы (рис.2.2), число которых равно ее порядку 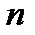. В общем случае входные 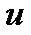и выходные переменные могут быть векторными величинами размерности и соответственно.

Координаты состояния х1, х2 , ... ,хn   u   y       Рис.2.2 - Состояние системы

Переменные состояния называют также координатами состояния, так как их совокупность задает вектор состояния .

 

Множество возможных положений этого вектора образует векторное пространство , называемое пространством состояний системы. В переменных состояния САУ описывается векторно-матричным уравнением

 

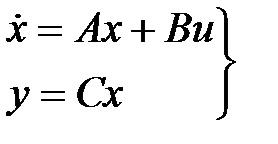, (2.17)

 

где - квадратная матрица коэффициентов (ее называют также собственной параметрической матрицей системы); - входная матрица (матрица управления) системы; - выходная матрица системы;

- вектор переменных состояния - внутренних координат системы;

- вектор входных переменных (управляющих и возмущающих);

- вектор наблюдаемых или выходных переменных; размерности матриц 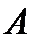, , 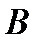, соответственно, ( ), ( ), ( ).

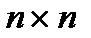Процессы в САУ в свободном движении (без внешних воздействий) согласно уравнению (2.17) описываются векторно-матричным уравнением с характеристическим уравнением , где - единичная матрица, или в развернутом виде системой дифференциальных уравнений

 

 

с характеристическим уравнением

 

. (2.18)

 

Эти уравнения при определенных начальных условиях дают возможность изучить процессы в системе путем их решения численными методами с использованием ЭВМ.

Разработаны различные способы перехода от уравнений типа «вход-выход» к уравнениям состояния вида (2.17) и наоборот. Один из наиболее распространенных способов состоит в следующем. Пусть САУ описывается уравнением (2.9). Введем обозначения

 

, , ... , ,

.

С помощью этих обозначений преобразуем уравнение (3.1) к следующему виду:

 

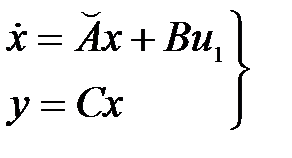, (2.19)

 

где ; ;

; .

В нашем примере и являются скалярными величинами. В общем случае (2.17) - это, соответственно, вектор наблюдаемых или выходных переменных и вектор входных переменных (управляющих и возмущающих), поэтому в (2.19) матрицы и выродились в вектор-столбец и вектор-строку соответственно.

Система уравнений (2.19) представляет собой описание линейной непрерывной системы в пространстве состояний . Уравнения (2.19) с матрицей называют уравнениями в форме Фробениуса.

Если , то

 

; .

 

Форма уравнений (2.19) с подобными матрицами и называется в ТАУ канонической формой фазовой переменной.

Задание 1

 

1.1. По дифференциальному уравнению системы:

Для каждого типового звена 1 – 12 (таблицы 2.1) в соответствии с его параметрами вывести дифференциальное уравнение, операторное уравнение, и выражение передаточной функции.

1.2Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.

Первая стандартная символическая форма операторно-структурное описание системы, т.е. в виде операторов звеньев.

Во второй стандартной форме записи дифференциального уравнения используется передаточная функция системы.

Третья стандартная форма записи дифференциального уравнения - переменные состояния.

 

Таблица 2.1 – Исходные коэффициенты

 

№ п.п.	Наименование звена	а 0	а 1	а 2	b0	b1	Примечания
	Безынерционное (пропорциональное)					к
	Инерционное 1-го порядка (апериодическое)		Т			k
	Инерционное 2-го по- рядка (апериодическое)	Т22	Т1			k	Т1³2Т2
	Инерционное 2-го по- рядка (колебательное)	Т22	Т1			k	Т1< 2Т2
	Идеальное интегрирующее					k
	Реальное интегри рующее	Т				k
	Идеальное дифферен- цирующее				k
	Реальное дифферен- цирующее		Т		k
	Изодромное (пропорционально - интегрирующее)				k1	k
	Форсирующее (пропорционально- дифференцирующее)				k1	k
	Интегро-дифференцирующее с преобладанием интегрирующих свойств		Т		k1	k	k1/k< T
	Интегро-дифференцирующее с преобладанием дифференцирующих свойсв		Т		k1	k	k1/k>T

Задание 2

 

2.1Для каждого звена (таблицы 2.2) по его передаточной функции записать дифференциальное уравнение.

2.2 Математическое описание типового звена системы автоматического регулирования записать в трех формах записи дифференциальных уравнений.

 

Таблица 2.2

Вар	Передаточная функция	Значения параметров передаточной функции
		а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3
		а0=1; а1=5; а2 =1,2; а3 =0,9; в0=1;в1=3; в2=0,8
		а0=1; а1=5; а2 =1,2; в0=1; в1=3;
		а0=1; а1=5; а2 =1,2; а3 =0,9; а4=0,5; в0=10
		а0=1; а1=5; а2 =1,2; а3 =0,9; в0=10
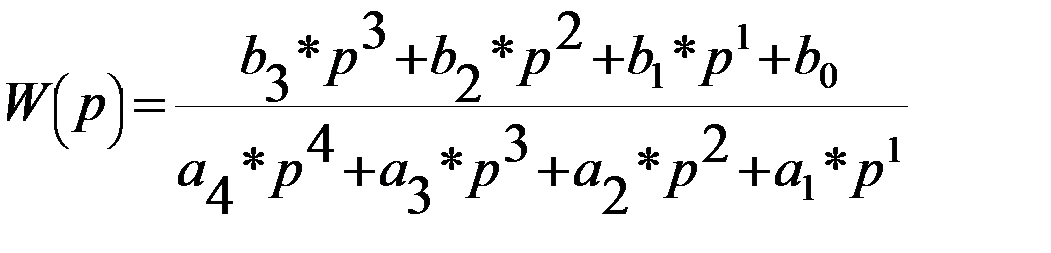
		а0=1; а1=5; а2 =1,2; а3=0,9;а4=0,5;в0=1;в1=3; в2=0,8;в3=0,3
		Т0=2; Т1=4; Т2=1,1;Т3=0,9
		Т0=2; Т1=4; Т2=1,1;Т3=1,1;Т4=,9
		К= 10;Т1=4; Т2=1,1;Т3=0,9
		К= 10; Т2=1,1;Т3=0,9 Т4=0,9
		Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5
		К=10 Т0=0,7; Т1=3;Т2=1,2;Т3=0,9;Т4=0,8;Т5=0,5;

 

Задание №3

3.1 Для заданной схемы необходимо составить операторное уравнение для каждого элемента схемы САУ.

3.2. Определить входные и выходные величины каждого элемента, и определить передаточные функции отдельных элементов функциональной схемы.
Формы записи дифференциальных уравнений.

3.3Сформировать математическое описание систем автоматического регулирования в виде структурной схемы в буквенном и числовом обозначениях.

3.4 Сформировать математическое описание систем автоматического регулирования в виде третьей стандартной формы записи дифференциального уравнения - В переменных состояния САУ описываемых векторно-матричным уравнением.

 

Вариант 1

 

Схема, показанная на рисунке 2.2, представляет собой САР температуры в помещении. Объектом регулирования (ОР) в дан­ной системе является помещение, для которого регулируемая ве­личина — температура внутри помещения Ө, регулирующее (уп­равляющее) воздействие — температура воздуха Ө_К, поступающего из калорифера, возмущающее воздействие — изменения внешних факторов f(в общем случае изменение температуры атмосферного воздуха, его влажности, скорости ветра). При исследовании сис­темы в качестве основного возмущения следует рассматривать из­менение температуры окружающего воздуха.

Воспринимающим органом — ВО (датчиком, чувствительным элементом) в данной САР является терморезистор R_Д, включен­ный в мостовую схему, обеспечивающую с помощью резистора R_Озадание необходимого значения температуры в помещении и выполняющую также функции сравнивающего органа — СО (эле­мента сравнения). Усиление сигнала разбалансаΔU(сигнала рас­согласования) измерительной мостовой схемы обеспечивается посредством усилителя. Усиленный сигнал Uобеспечивает вра­щение двухфазного исполнительного двигателя, который изменя­ет перемещение клапана (заслонки) на трубопроводе подачи парав калорифер, чем достигается изменение температуры воздуха на входе калорифера — регулирующего воздействия на объектерегулирования.

 

 

 

1 - помещение; 2 - теплообменник (калорифер), 3 - измерительная мостовая схема; 4 - двухфазный ис­полнительный двигатель, 5 — дифференциальный магнитный усилитель; 6 — клапан (заслонка)

 

Рис. 2.2. Схема САР температуры

 

Динамические свойства объекта регулирования и элементов системы описываются следующими уравнениями:

 

где То, Т2, Т3, Т4 — постоянные времени, с; Ө — значение температуры воздуха в помещении, °С, Ө к — значение температуры воздуха на выходе калорифера, °С; к, к₁, к₂, к₃, к₄— коэффициенты передачи; f— возмущающее воздействие на объекте регулирования; Uд —падение напряжения на термодатчике, В; ΔU— напряжение на выходе мостовой схемы (сигнал рассогласования), В; μ. — линейное перемещение клапана, см; U₀ — задающий сигнал, В.

Значения параметров элементов САР по вариантам даны в таб­лице 2.3.

Заданное значение температуры в помещении Ө = 20 °С.

 

Табл.2.3.

Значения параметров элементов САР

Вариант	Т0, с	Т2, с	к	к1, В/0С	к4	к2, см/(В*с)	f,.0С	К3, °С/см
		0,06	0,2	0,2		0,002	-11
		0,07	0,25	0,3		0,001
		0,08	0,3	0,25		0,0018	-8
		0,09	0,35	0,2		0,002
		0,10	0,4	0,2		0,002	-5
		0,50	0,18	0,25		0,003
		0,055	0,19	0,4		0,0035
		0,06	0,17	0,4		0,0025	-15
		0,06	0,25	0,2		0,0016
		0,08	0,4	0,15		0,0014	-18

Примечание. Для всех вариантов постоянные времени Т3 = 20 с, Т4=0,5 с.

 

Вариант 2

 

Схема САР, приведенная на рисунке 2.3, обеспечивает стаби­лизацию угловой скорости электродвигателя постоянного тока который совместно с рабочим механизмом является объектом ре­гулирования. Регулируемая величина объекта — угловая скорость двигателя ω, регулирующее воздействие — напряжение Uг,пода­ваемое от генератора на якорь двигателя. Возмущающее воздейст­вие на объекте регулирования — момент сопротивления М_с, соз­даваемый рабочим механизмом. Угловая скорость двигателя ωконтролируется тахогенератором, сигнал которого Uтг, пропор­циональный скорости, сравнивается с задающим сигналом U₃. Сигнал рассогласования ΔU = U₃— U_Tг усиливается магнитным усилителем и воздействует на обмотку возбуждения генератора, выполняющего функции исполнительного органа (элемента).

Динамические свойства объекта регулирования и элементов САР описываются следующими уравнениями:

гдеТ_д, Ту, T_v — постоянные времени, с; К_д, К_м, К_тг, К_у, К_г — коэффициенты передачи соответствующих элементов систем

 

 

1 — задающий потенциометр; 2 — магнитный усилитель; 3 — генератор; 4 — двигатель; 5 — тахогенератор; 6 — рабочий механизм

Рис. 2.3. Схема САР угловой скорости электродвигателя

 

Табл.2.4

Значения параметров элементов САР

 

Вари­ант	Ту, с	Ку	Кг	Тг, с	Кд, рад/ с*В	Тд, с	Км рад/ с*Н* м	Мс, Н*м	Кгг, В*с/ рад
	0,020	4,0	2,0	0,10	1,0	0,5	0,02		1,0
	0,015	5,0	1,8	0,12	0,95	0,60	0,03		0,9
	0,018	4,5	1,7	0,15	0,85	0,70	0,04
	0,022	6,0	1,5	0,20	0,8	0,80	0,05		0,7
	0,020	5,8	1,6	0,16	1,5	0,65	0,06		0,6
	0,025	4,2	2,0	0,25	1,4	0,75	0,07		0,5
	0,020	3,5	2,7	0,22	1,3	0,80	0,08		0,4
	0,028	6,2	2,1	0,30	1,2	0,75	0,02		0,5
	0,018	6,5	2,3	0,16	1,0	0,50	0,013		0,6
	0,014	7,0	2,5	0,20	1,25	0,80	0,015		0,7

Значения параметров объекта регулирования и элементов сис­темы для различных вариантов указаны в таблице 2.4. Заданное значение угловой скорости ω = 40 рад/с.

 

 

 

 

Вариант 3

На рисунке 2.4 изображена схема САР давления Р в ресивере (воз­духосборнике) 1, который является в данной системе объектом регу­лирования. Давление в ресивере регулируется посредством изменения количества воздуха Q, зависящего от положения заслонки 2, т.е. от ее линейного перемещения Х₃, которое можно рассматривать как регу­лирующее воздействие на входе объекта регулирования. Внешним возмущением, вызывающим отклонение регулируемой величины — давления Р, является изменение расхода сжатого воздуха Q_c.

Рис 2.4 Схема САР давления Р в ресивере

 

Давление в данной системе контролируется с помощью сильфонного датчика 3, выход­ная величина которого — пере­мещение Х_с сильфона 5 одно­значно зависит от разности сил ΔF= F₀- F_p, где F_p- сила, соз­даваемая давлением Р, F₀— си­ла натяжения пружины 6, кото­рое можно изменять винтом 7.

 

Перемещение сильфона Х_сс помощью потенциометрического преобразователя 4 преобразуется в электрический сигнал — напряжение U, которое усиливается электронным усилителем 8. Выходной сигнал усилителя U_yуправляет электромагнитным при­водом 9, связанным с заслонкой 2,

 

В данной САР сильфонный датчик выполняет функции вос­принимающего, задающего и сравнивающего органов. Как вос­принимающий орган он контролирует давление Р, преобразуя его в силу Fp. Задание требуемого давления в ресивере обеспечивается посредством силы F0. Как сравнивающий орган сильфон обеспе­чивает сравнение величин F0 и Fp, в результате чего, как отмеча­лось ранее, получается ΔF= F0 — Fp — сигнал рассогласования.

 

Динамические свойства объекта регулирования и элементов САР описываются следующей системой уравнений:

 

 

заслонкой

 

Физическая сущность переменных, входящих в уравнения, от­ражена выше в описании схемы САР. Параметры T0, T1, T2, T3 и К0, Кq, Кв, Кc, Кп, Ку, К₃ — соответственно постоянные времени и ко­эффициенты передачи. Их размерности и значения по вариантам даны в таблице 2.5. Требуемое значение давления Р = 500 кПа.

 

Таблица.2.5

 

Значения параметров элементов САР

Вари­ант	Т0,с	Ко КПа/мм	Т1,с	Т2,с	Кс мм/Н	Кв Н/кПа	КQ, Кпа*с/м3	ΔQC, м3/с	Кп В/мм	Ку	Т3	К3 Мм/В
	1,3		0,2	0,045	2,5	0,5		0,1	0,2		0,01
			0, 25	0 ,04	2,5	0,5		-0, 2	0,2		0,01
	0,6	3,5	0,34	0,022	2,5	0,5		0,3	0,2		0,01
		4,8	0,25	0,035	2,5	0,5		-0,15	0,2		0,01
	0,7	4,5	0,3	0,04	2,5	0,5		0,12	0, 9		0,01
	0,8	3,5	0,18	0, 025	2 ,5	0,5		-0,2	0 ,2		0,01
	0,4	4,4	0,25	0,03	2,5	0,5		0,11	0,2		0,01
	0,65	5,5	0,2	0,02	2,5	0,5		-0,12	0,2		0,01
	0, 7		0, 4	0 ,025	2,5	0,5		0,14	0,2		0,01
	0,55		0,25	0,035	2,5	0,5		-0,14	0,2		0,01

 

Вариант 4

На электрических станциях при производстве электроэнергии предъявляют определенные требования к стабильности частоты f генерируемой ЭДС. Частота f однозначно определяется угловой скоростью ω рабочего колеса гидротурбины. В связи с этим гид­ротурбины на электростанциях оснащают САР угловой скорости. На рисунке 2.5 показана схема одного из вариантов такой САР.

В данной системе объектом регулирования является гидротур­бина 1, регулируемой величиной — угловая скорость ω .Она при постоянном расходе воды изменяется в зависимости от нагрузки на валу турбины, т. е. от мощности Р, которая потребляется от ге­нератора 2 (с увеличением мощности угловая скорость снижается, с уменьшением — возрастает). Таким образом, мощность Р явля­ется внешним возмущающим воздействием на объекте регулиро­вания. Для регулирования угловой скорости предусмотрена за­слонка 3, с помощью которой изменяется расход воды через тур­бину. Он однозначно зависит от вертикального перемещения X заслонки. Следовательно, перемещение заслонки X можно рас­сматривать как регулирующее воздействие объекта регулирова­ния. Угловая скорость ω контролируется посредством тахогенератора 4, ЭДС Е которого сравнивается с задающим напряжением U0. Сигнал рассогласования Δ U через усилитель 5 управляет по­средством электродвигателя 6 и редуктора 7 заслонкой 3.

 

 

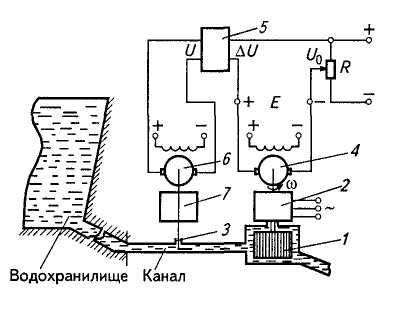
Рис. 2.5 Схема САР угловой скорости рабочего колеса гидротурбины

 

Динамические свойства элементов САР описываются следую­щей системой уравнений:

 

Гидротурбина:

 

 

Тахогенератор:

Е = Кт*ω

Сравни­вающий орган:

Δ U= U0 - Е

Электронный усилитель:

U= ky*Δ U

 

Электродвигатель совместно с заслонкой

Таблица.2.6

Значения параметров элементов САР

 

Вари­ант	То, с	К0 Рад/с* см	К1 Рад/с* кВт	Кт В*с/ рад	Ку	Р, кВт	Тм, с	Тя, с	Кэ, см/(с • В)
	0,1		0,01	1,0		-100	0,02	0,005	0,02
	0,15		0,015	1,0			0,019	0,004	0,02
	0,11		0,016	1,0		-70	0,018	0,003	0,02
	0,12		0,01	1,0			0,017	0,002	0,02
	0,15		0,01	1,0		-95	0,016	0,002	0,02
	0,2		0,011	1,0			0,015	0,002	0,02
	0,1		0,015	1,0		-75	0,014	0,002	0,02
	0,14		0,018	1,0			0,02	0,005	0,02
	0,16		0,01	1,0		-100	0,018	0,003	0,02
	0,18		0,01	1,0			0,016	0,002	0,02

 

Методический пример№1

Рассмотрим в качестве примера составление математической модели двигателя постоянного тока с независимым возбуждением (рис. 2.6), который часто используется в системах автоматического управления. Здесь – напряжение, подаваемое на якорь двигателя, которое будем считать входным воздействием; – ток в цепи якоря, представляющий собой внутреннюю переменную объекта; – сопротивление и индуктивность цепи якоря; – противоЭДС, т. е. напряжение, возникающее в обмотке якоря в результате его вращения в магнитном поле; – скорость вращения двигателя, которую будем считать выходной переменной; ОВД – обмотка возбуждения двигателя.

 

 

R,L

I

U

я

w

ОВД

E

 

Рис 2.6 Схема двигателя постоянного тока

 

Запишем основные уравнения, характеризующие процессы в двигателе. Уравнение электрического равновесия якорной цепи имеет вид

Уравнение равновесия моментов на валу двигателя следующее:

где – приведенный момент инерции; – вращающий момент; – момент сопротивления на валу двигателя, который является возмущающим воздействием.

С достаточной степенью точности во многих случаях можно считать, что 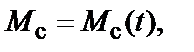где В результате уравнения двигателя принимают вид

введем следующие обозначения: – управление; – переменные состояния; – возмущение. запишем уравнения двигателя в переменных состояния

где

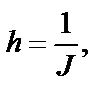
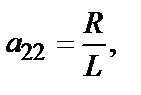
Часто модель двигателя представляют в виде одного дифференциального уравнения

Здесь – электромеханическая постоянная времени двигателя; – электромагнитная постоянная времени якорной цепи; – коэффициент усиления; .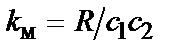

 

Методический пример№2

Рассмотрим перевернутый маятник, ось которого монтируется на тележке (каретке), перемещающейся в горизонтальном направлении . В совокупности такое устройство представляет собой объект управления, называемый «кареткой – маятником». Его схематичная модель изображена на рис. 2.7.

Рис. 2.7. Объект управления «каретка–маятник»

 

Здесь – угол отклонения маятника (выходная переменная);
– прикладываемая управляющим двигателем сила (входная переменная); – перемещение каретки; – масса каретки; L – расстояние между осью и центром тяжести маятника; – масса маятника; J – момент инерции относительно центра тяжести; g – ускорение силы тяжести; и – горизонтальная и вертикальная силы реакции у оси маятника.

Упрощенная модель объекта «каретка – маятник» может быть представлена системой дифференциальных уравнений

 

 

где – эффективная длина маятника.

Перейдем к описанию модели объекта в переменных состояния. В качестве компонент вектора состояния выберем следующие величины:

а выходной переменной объекта является угол отклонения маятника В результате уравнения состояния принимают вид

теперь определим матрицы объекта:

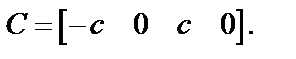
Контрольные вопросы

1.Какой режим САУ называется динамическим?

2.Что называется регулированием?

3.Назовите возможные виды переходных процессов в САУ. Какие из них являются допустимыми для нормальной работы САУ?

4.Что называется уравнением динамики? Каков его вид?

5.Как провести теоретическое исследование динамики САУ?

6.Что называется линеаризацией?

7.В чем геометрический смысл линеаризации?

8.В чем состоит математическое обоснование линеаризации?

9. Запишите линеаризованное уравнение динамики в обычной и в операторной формах?

10. В чем смысл и какими свойствами обладает дифференциальный оператор p?

11.Что называется передаточной функцией звена?

12.Запишите линеаризованное уравнение динамики с использованием передаточной функции. Справедлива ли эта запись при ненулевых начальных условиях? Почему?

14.Что назы