Пример построения логарифмических частотных характеристик статической системы управления

Проведем построение ЛЧХ для статической СУ, имеющей ПФ

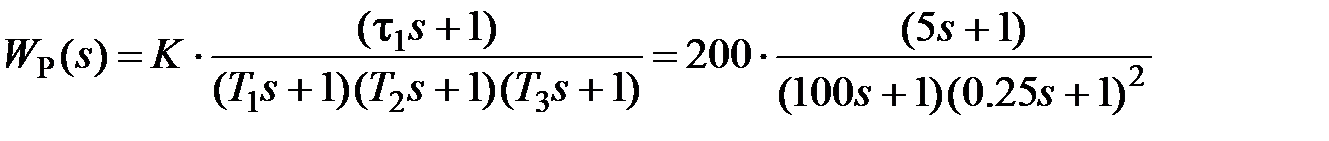. (11.5)

 

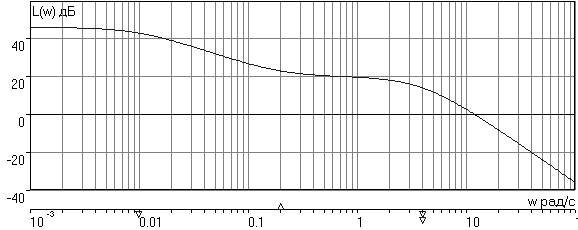
Построение ЧХ отображено на рис. 11.15. После оцифровки оси частот и нанесения на сетку ЛАХ вертикальных штриховых линий сопряжения начинается построение собственно ЛАХ LP(w). Слева от минимальной частоты сопряжения wc,min= wc1=1/T1= 0.01 рад/с, определяемой самой большой постоянной времени в СУ, формируем низкочастотный участок ЛАХ. В данном

случае это прямая, параллельная оси частот и проходящая на расстоянии 20lg200 = 20lg(10*10*2) = 20lg10 + 20lg10 + 20lg2 = = 20дБ + 20дБ + 6дБ = 46дБ.

 

L(w) дБ

wc1=1/T1

j (w) O

wc2=1/t1

wc3=1/T2 =1/T3

-20

1/(T2s+1), 1/(T3s+1)

(t1s+1)

1/(T1s+1)

w

-40

20lgK 46 дБ

jP(w)

LP(w)

 

Рис. 11.15

Линия сопряжения wc1соответствует полюсу 1/T1. Поэтому переход через нее асимптотической ЛАХ в сторону увеличения частоты сопровождается изменением наклона на –20 дБ/дек. Прямую с таким наклоном проводим до следующей частоты сопряжения wc2= 0.2 рад/с, которая соответствует нулю 1/t1, и переход через нее асимптотической ЛАХ в сторону увеличения частоты сопровождается изменением наклона на +20 дБ/дек. В результате суммарный наклон следующего участка ЛАХ будет составлять 0 дБ/дек; параллельный оси частот участок ЛАХ следует продолжить до частоты сопряжения wc3= 4 рад/с. На линии сопряжения этой частоты “срабатывают” два полюса, так как “включаются” два апериодических звена с одинаковыми постоянными времени. Переход через эту линию сопровождается изменением наклона на 2*(-20 дБ/дек) = -40 дБ/дек. В результате окончательный наклон ЛАХ справа от wc3= 4 рад/с равен -40 дБ/дек.

ФЧХ j P(w) формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см. рис. 11.15.

Логарифмические частотные характеристики имеют большое практическое значение. Поэтому рассмотрим их построение. Часто результирующую передаточную функцию смешанного соединения звеньев можно свести к виду

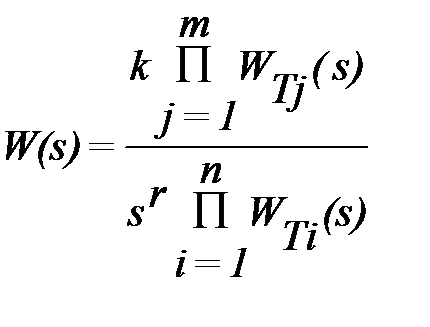, (11.6)

 

где W_T(s) - передаточная функция типового звена.

В этом случае построение ЛАХ производится по выражению

 

L(w) = 20lgA(w) = 20lg|W(jw)|=

= 20lgk - r´20lgw + - .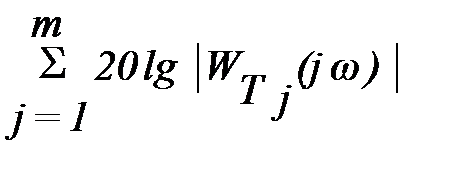

Построение ЛФХ производится по выражению

y(w) = argW(jw) = -r´90⁰ + - .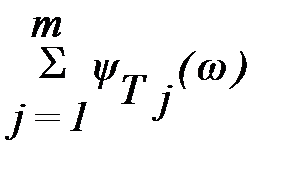

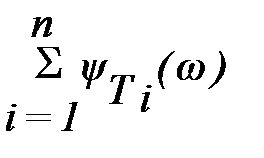Таким образом, результирующая ЛАХ определяется суммированием ЛАХ составляющих типовых звеньев, а результирующая ЛФХ - соответственно суммированием ЛФХ составляющих типовых звеньев. Таблицы характеристик типовых звеньев имеются в литературе.

Асимптотические ЛАХ можно построить непосредственно по виду передаточной функции по следующему правилу, состоящему из четырех пунктов.

1. Частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:

.

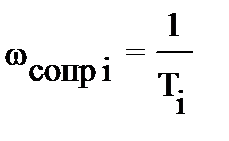Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше.

2. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, имеет наклон -(20´r)дб/дек и проходит через точку с координатами: w=1 с^{-1, L(1)=20lg k дб, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции.}

3. На сопрягающих частотах ЛАХ претерпевает изломы.

3.1. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на -(20´v)дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

3.2. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20´v) дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

4. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.

Пример. Построить логарифмические амплитудную и фазовую частотные характеристики разомкнутой линейной системы с передаточной функцией

 

 

при K = 500; Т1= 0,05с; Т2= 0,017с; Т3= 0,0025с; Т4= 0,001с.

Решение

 

Предварительно заполните таблицу, подобрав к каждому алгоритму конкретное соответствие из данного задания.

 

№ п/п	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Представить передаточную функцию САУ в частотном виде.	Частотная передаточная функция САУ имеет вид
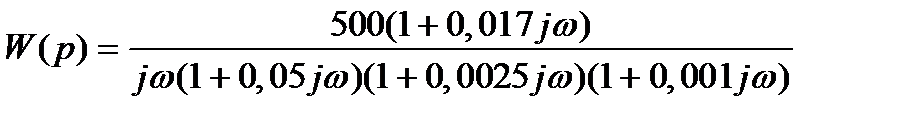
	Определить ординату ЛАЧХ на частоте w = 1 и значения асимптотических частот.	При w = 1ордината результирующей ЛАЧХ равна 20 lg K = 54. Значения асимптотических частот равны: w1 =1/T1 = 20(1/c), w2 = 1/T2 = 59(1/c), w3 = 1/T3 = 400(1/c), w4 = 1/T4 = 1000(1/c).
	Построить асимптотическую ЛАЧХ в соответствии с правилами.	Передаточная функция содержит одно интегрирующее звено, поэтому первую асимптоту проводим с наклоном –20 дБ/дек через точку с координатами (w = 1, L = 54) до ординаты на частоте w1 = 20(1/c). Здесь асимптотическая ЛАЧХ меняет наклон еще на –20 дБ/дек и с наклоном –40 дБ/дек идет до ординаты на частоте w2 = 59(1/c). Здесь асимптотическая ЛАЧХ меняет наклон на +20 дБ/дек и с наклоном –20 дБ/дек идет до ординаты на частоте w3 = 400 (1/c). Здесь асимптотическая ЛАЧХ меняет наклон на –20 дБ/дек и с наклоном –40 дБ/дек идет до ординаты на частоте w4 = 1000 (1/c), после которой она с наклоном –60 дБ/дек идет до –¥.

№ п/п	Алгоритм	Конкретное соответствие данной ситуации предложенному алгоритму
	Уточнить ЛАЧХ с учетом поправок.	К асимптотической ЛАЧХ прибавляем поправки для каждого элементарного звена (значения поправок приводятся в справочниках и определяются по специальным номограммам или таблицам*). Эти поправки для апериодических звеньев и дифференцирующего звена первого порядка одинаковы, но только разных знаков, и на асимптотической частоте имеют значение по модулю равное 3 дБ/дек.
	Пос­троить ЛФЧХ	Фазовая частотная характеристика системы определяется выражением 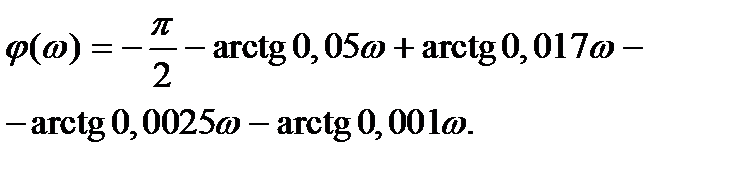ЛФЧХ определяем как сумму ординат фазовой частотной характеристики интегрирующего звена, трех апериодических звеньев и дифференцирующего звена первого порядка (фазовые характеристики элементарных звеньев имеют стандартный вид и имеются в справочниках в виде номограмм или таблиц).

 

Задания:

- построение ЛАЧХ системы ;

- построение ЛФЧХ системы;

- определение устойчивости линейной системы по логарифмическим частотным характеристикам

 

 

Задача №1 Рассчитать устойчивость линейной системы по логарифмическим частотным характеристикам, заданной следующей структурной схемой (рис 11.16) .

 

 

Рис. 11.16

 

W₁(P)=k₁; W₂(P)= ;W₃(P)= 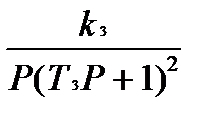; W₄(P)= .

Параметры звеньев: k₁=12; k₂=80; k₃=0.15; k₄=2; T₂=0.5; T₃=10; T₄=2.

 

Задача № 2

Рассчитать устойчивость линейной системы по логарифмическим частотным характеристикам, заданной следующей структурной схемой (рис 11.17-11.21) .

 

Схема № 2.1.

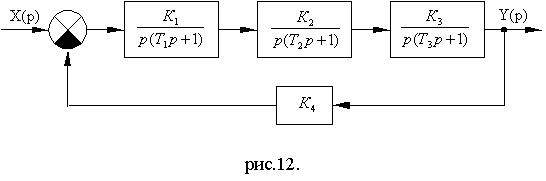
Рис. 11.17

 

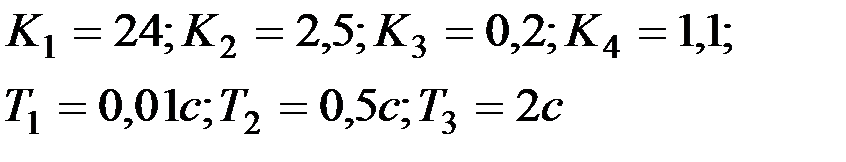
Вариант № 0	Вариант № 1
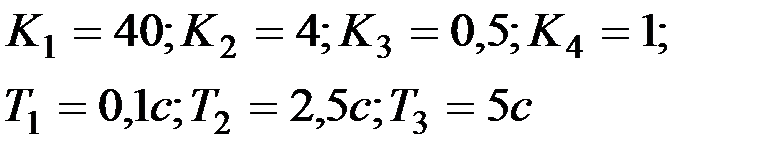
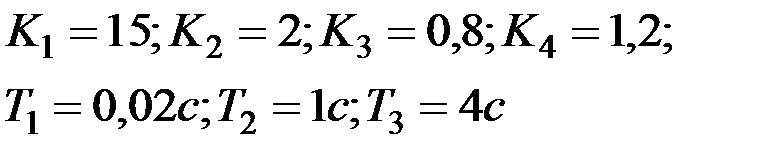
Вариант № 10	Вариант № 11
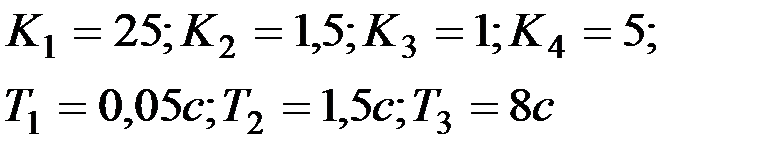
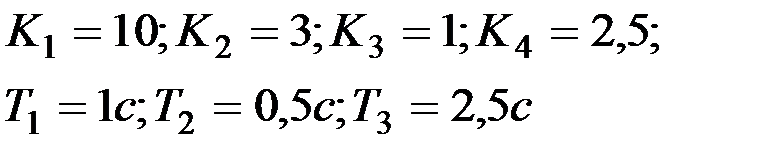
Вариант № 12	Вариант № 13
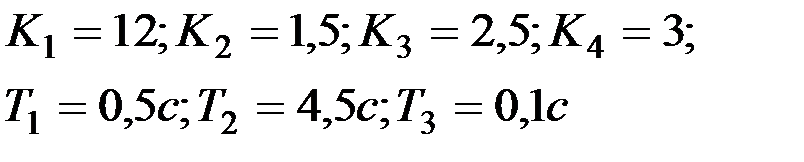
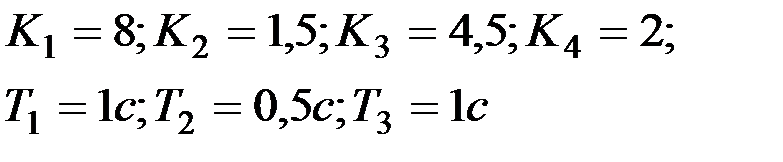
Вариант № 14	Вариант № 15

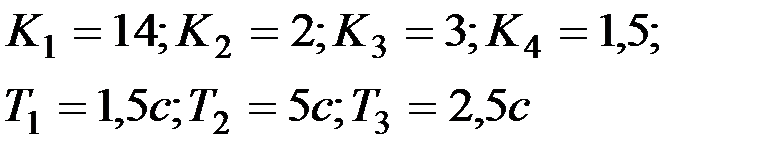
Схема № 2.2.

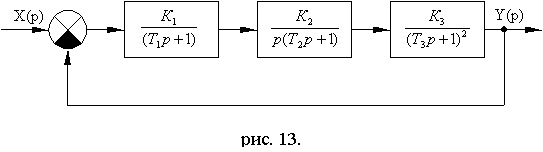
Рис. 11.18

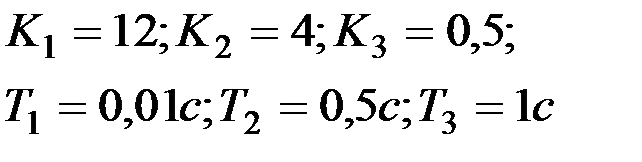
Вариант № 2	Вариант № 3
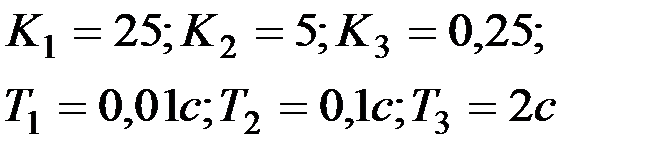
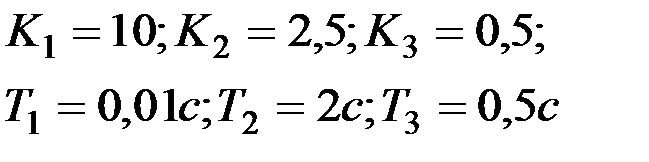
Вариант № 16	Вариант № 17
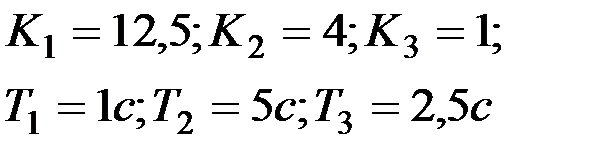
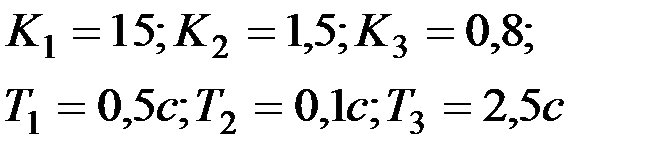
Вариант № 18	Вариант № 19
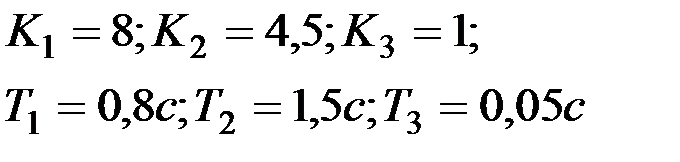
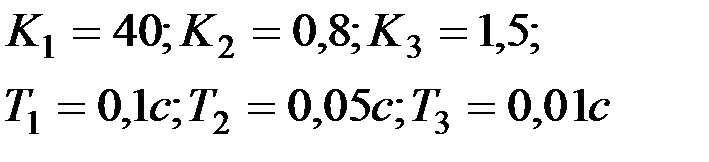
Вариант № 20	Вариант № 21

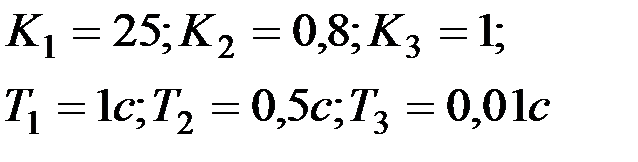
Схема №2. 3

 

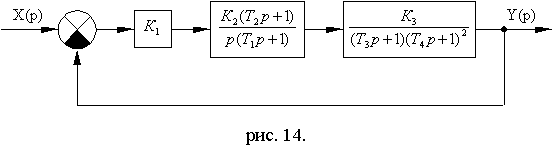
Рис. 11.19

Вариант № 4	Вариант № 5
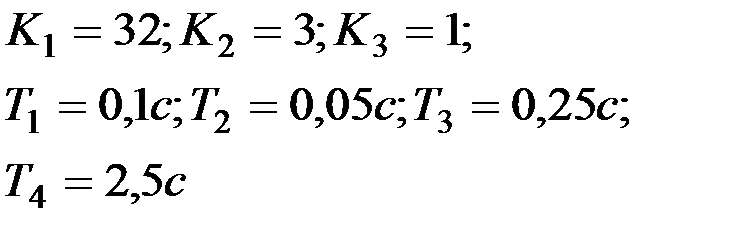
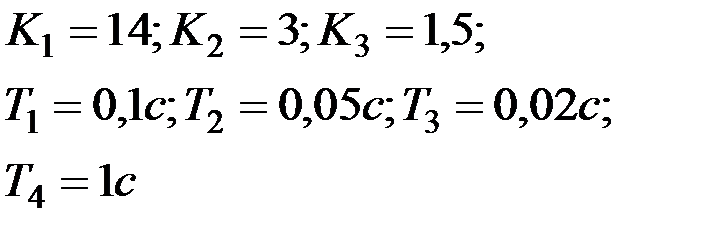
Вариант № 22	Вариант № 23
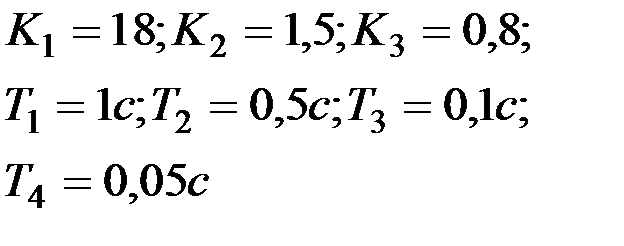
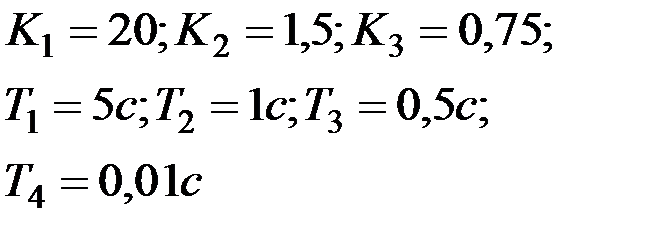
Вариант № 24	Вариант № 25

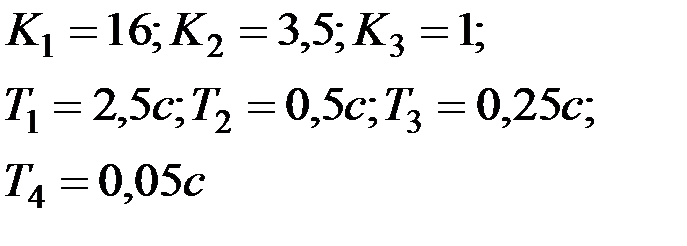
Схема№ 2.4

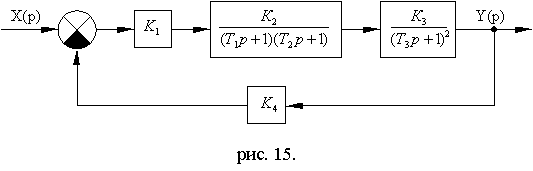
Рис. 11.20

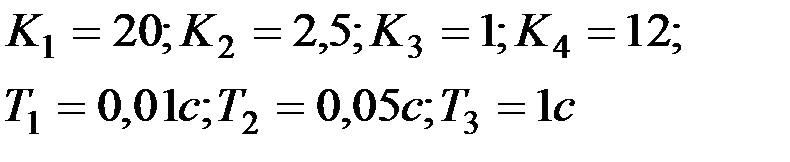
Вариант № 6	Вариант № 7
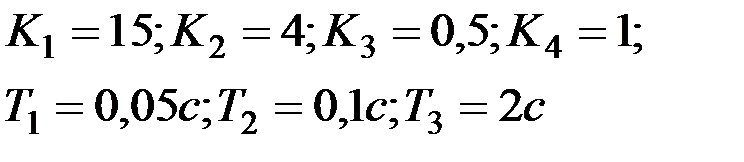
Вариант № 26	Вариант № 27

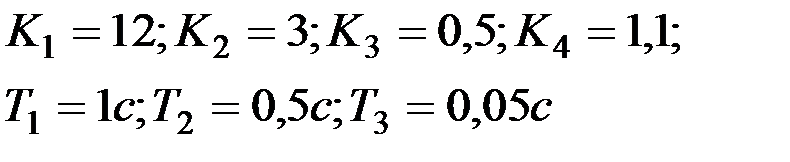
Схема № 2.5

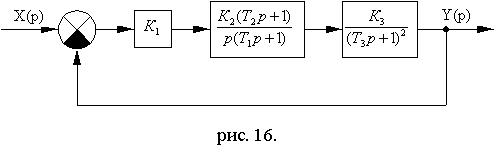
Рис. 11.21

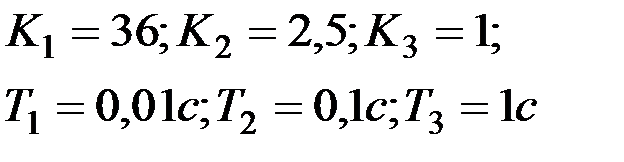
Вариант № 8	Вариант № 9
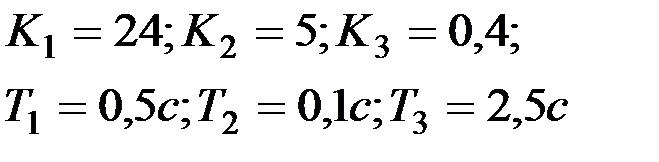
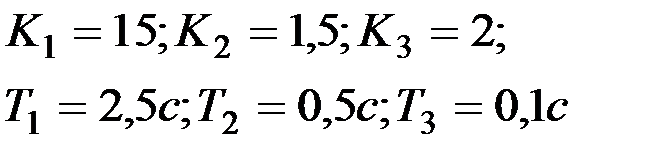
Вариант № 28	Вариант № 29

 

 

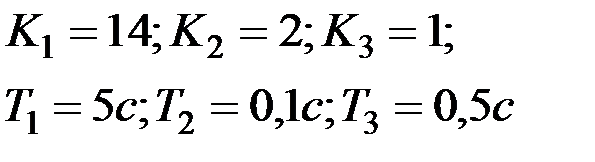
Практическая работа № 12

«Определение областей устойчивости по одному и

Двум параметрам»

 

Цель работы:Исследовании влияния различных параметров САУ на ее устойчивость методом D- разбиения в плоскости одного и двух параметров

 

Общие сведения

 

При проектировании САУ обычно требуется определить влияние значений каких-либо изменяемых параметров на устойчивость. Для этого строят область устойчивости системы в пространстве изменяемых параметров. Область устойчивости определяет совокупность значений параметров системы, при которых она устойчива.

 

Рисунок 12.1 - Область устойчивости

Если варьируемых параметров два ( 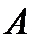, ), то область устойчивости изображается на плоскости (рисунок 12.1). На рисунке линией изображена граница устойчивости. Для указания, с какой стороны границы находится область устойчивости, вдоль нее наносится штриховка, которая обращена в сторону области устойчивости.

Каждая точка , внутри области определяет комбинацию параметров, при которых система устойчива. Все пространство вне области устойчивости называется областью неустойчивости. Все ее точки соответствуют значениям параметров, при которых система неустойчива. В общем случае при варьируемых параметрах область устойчивости представляет собой гиперповерхность в 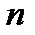-мерном пространстве.

Критерии устойчивости дают возможность при заданных параметрах САУ судить только о том, устойчива САУ или нет. Они позволяют также проследить влияние изменения некоторых параметров на устойчивость САУ. Для исследования влияния различных параметров САУ на ее устойчивость разработаны специальные методы, основанные на анализе перемещения корней характеристического уравнения в комплексной плоскости и построении корневых годографов или областей устойчивости САУ в пространстве параметров САУ.

Метод корневого годографа. Корневым годографом называется геометрическое место корней характеристического уравнения при изменении одного из параметров САУ от до . Характеристическое уравнение замкнутой САУ представляется в виде , где - переменный параметр САУ ( 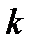или 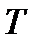). Далее, изменяя от до , необходимо найти перемещение всех корней характеристического уравнения.

Другие параметры звеньев САУ заданы и определяются из условий конкретной реализации САУ.

Если при изменении от до при определенном корень характеристического уравнения попадает на мнимую ось, то САУ будет на границе устойчивости; при тех , когда часть корней переходит слева направо мнимую ось, САУ будет неустойчива. Предложены правила, которыми пользуются при исследовании влияния параметров САУ на ее устойчивость методом корневого годографа.

Метод корневого годографа из-за сложности и малой наглядности получил незначительное распространение.

Критерий Вышнеградского

Впервые область устойчивости системы прямого действия в плоскости двух коэффициентов уравнения была построена русским ученым И.А. Вышнеградским .

Иногда ее называют критерием Вышнеградского для характеристического уравнения 3-го порядка:

или в его нормированном виде (форме Вышнеградского):

,

где 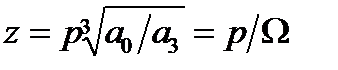- новая переменная,

- среднегеометрический корень,

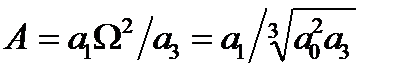; - параметры Вышнеградского.

Согласно критерию Гурвица, при и условие устойчивости задается определителем :

.

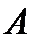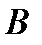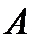Но Вышнеградский вывел это условие за 20 лет до Гурвица. На плоскости параметров и (рисунок 12.2) наносится граница устойчивости (равнобокая гипербола Вышнеградского с осями координат в качестве асимптот - изображение мнимой оси в плоскости параметров и ).

Область устойчивости САУ лежит выше кривой . Вышнеградский построил и другие кривые для определения вида (характера) переходного процесса (рисунок 12.2): I - область, соответствующая апериодическому затухающему процессу, II - монотонному затухающему процессу колебательного характера, III - периодическому затухающему процессу, IV - неустойчивому переходному процессу. Впоследствии диаграмма Вышнеградского была дополнена другими линиями: степени затухания, интенсивности процессов и т.д.

 

 

Рисунок 12.2 - Критерий Вышнеградского

 

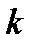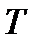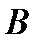Недостаток критерия Вышнеградского- параметры САУ ( или ) в неявном виде входят в выражения коэффициентов и , следовательно, чтобы определить поведение САУ при изменении одного или двух параметров, требуется трудоемкая дополнительная работа. Кроме того, есть ограничение на порядок САУ: уравнение САУ должно быть не выше 3-го порядка.

Метод D-разбиений разработан Ю.И. Неймарком. В этом методе используется характеристическое уравнение замкнутой САУ :

; .

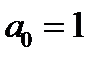При :

,

где , 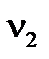- исследуемые параметры.

Построение области устойчивости в плоскости одного комплексного параметра методом D-разбиений. Выясним влияние одного параметра ( или ) на устойчивость САУ. Пусть некоторые из коэффициентов характеристического уравнения зависят линейно от параметра . Тогда характеристическое уравнение САУ можно записать в следующем виде:

 

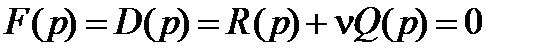. (12.1)

 

В (12.1) параметр входит линейно, и - многочлены от . При 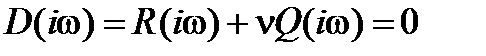, откуда 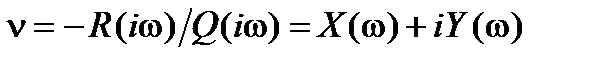. Изменяя от до и вычисляя и , построим границу D-разбиения (рисунок

12.3).

 

iY

a

b

X

с

I

II

III

V

IV

w®0

w®0

w=±¥

d

n=T

iY

X

I

-1

a

b

n=kp

w=0

w®¥

w®-¥

 

а) б)

 

 

Рисунок 12.3- D-разбиение для одного параметра:

а) одна область устойчивости; б) две области устойчивости

 

Граница D-разбиения - геометрическое расположение мнимой оси в плоскости одного параметра. Переход через границу D-разбиения означает переход через мнимую ось. Практически интересуются D-разбиением не на всей плоскости, а лишь на ее действительной оси, соответствующей действительным значениям ( или ), т.е. нас интересует отрезок устойчивости на вещественной оси, хотя в общем случае и может рассматриваться во всей области комплексного параметра.

Кривая D-разбиения делит плоскость на ряд областей, например на I-V (рисунок 12.3, б).

Штриховка кривой D-разбиения производится слева при изменении отминус до , что соответствует положению мнимой оси в координатной системе и расположению левых устойчивых корней. Из рисунка12.3 следует, что претендент на область устойчивости - область I, окруженная штриховкой. Отрезок устойчивости 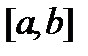- область изменения для устойчивой САУ (рисунок 12.3 а, б). Для проверки в области устойчивости I берется любое значение на отрезке и одним из критериев осуществляется проверка факта устойчивости САУ. Если при данном САУ устойчива, то область I - область устойчивости. На рисунке 12.3 - область IV также является областью устойчивости (отрезок устойчивости 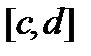). Обычно задачу D-разбиения решают с помощью ЭВМ.

Построение области устойчивости в плоскости двух параметров.

При проектировании САУ часто требуется выявить влияние на устойчивость не одного, а двух параметров и ( и ). Предположим, что эти параметры входят линейно в характеристическое уравнение замкнутой САУ.

Порядок построения кривой D-разбиения следующий. Выделяют две составляющие характеристического уравнения САУ , линейно зависящие от параметров и . Это уравнение запишется в следующем виде:

 

.

 

При

,

 

где , ,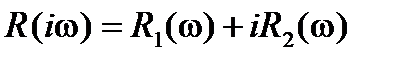

.

Здесь

,

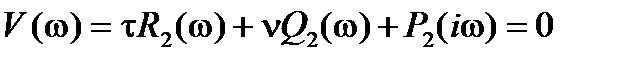- соответственно, вещественная и мнимая части.

В результате получают два параметрических уравнения с двумя неизвестными и . Решая эти уравнения относительно и , получим

 

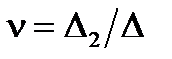; , (12.2)

 

где ,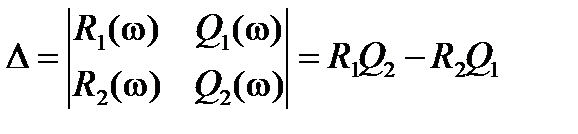

 

,

 

.

 

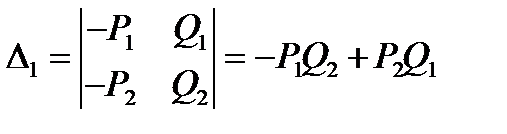По этим уравнениям для каждого определяют и , затем, исключая промежуточный параметр , строят границу D-разбиения в плоскости двух параметров и (рисунок 12.4).

Определители , , - нечетные непрерывные функции , так как вещественные части , , - четные функции, а мнимые части , , - нечетные.

Отсюда следует, что и - четные функции , т.е. можно ограничиться рассмотрением положительных значений частот от до .

 

n

t

I

D<0

D>0

w¹0,D=0

D>0

n

t

wi

D>0

ОП

w¹0,D=0

n

t

t1

V1

I

ОП

D

ОП

w=0

w®¥

n

t

I

w=0

ОП

I

n

t

ОП

D>0

D>0

D=0

w=0

 

а) б)

 

 

в) г)

 

 

д)

 

Рисунок 12.4 - Примеры D-разбиения для двух параметров

 

Если при некоторых частотах определитель = 0, а и ¹ 0, то уравнения (12.2) уже не являются линейно независимыми и вырождаются в одно уравнение, а точки границы D-разбиения в плоскости и уходят в . Знак может измениться только при и 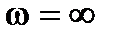. Если при некоторых = 0 (при всегда = 0) и = =0 (если =0 то и =0), то и будут неопределенными. Параметрические уравнения (12.2) становятся эквивалентными и определяют собой прямую в плоскости и , называемую особой прямой (ОП). ОП (или «концевые ОП») обычно соответствуют значениям и . В этом случае и зависят от и , т.е. и , и для получения уравнений ОП необходимо и приравнять к нулю ( - дает ОП при , а - для ).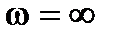

Правила штриховки границы D-разбиения. Граница D-разбиения в плоскости и штрихуется слева при 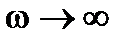, если > 0, и справа, если < 0. Так как граница D-разбиения для + и минус совпадает ( и четные функции , а - нечетная функция), то она штрихуется дважды с одной и той же стороны (рисунок 12.4 а). Штриховка концевых ОП одинарная и производится так, чтобы вблизи точки сопряжения прямой и кривой заштрихованные и незаштрихованные стороны были направлены друг к другу (рисунок 12.4 а, б, в). ОП служат дополнительной границей определения области устойчивости. Концевые ОП соответствуют апериодической границе устойчивости. Кроме концевых ОП существуют промежуточные ОП (при и 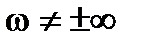), когда пара комплексных корней попадает на границу устойчивости (обычно для САУ с ). Следовательно, эти ОП соответствуют колебательной границе устойчивости и имеют двойную штриховку. Если , =0, а переходит через 0 и меняет знак, то появляется ОП, штрихуемая по изложенному выше правилу, но двойной штриховкой (рисунок 12.4 г). Если при , =0, а , пройдя через 0, не меняет знак, то ОП не штрихуется и выбрасывается из рассмотрения, т.е. ОП не является дополнительной границей устойчивости и вычерчиванию не подлежит (рисунок 12.4 д). На этом рисунке ориентация штриховки ОП показана условно, исходя из общих положений о штриховке ОП. При рассмотрении D-разбиения по двум параметрам следует правильно ориентировать оси. Для приведенной выше формы записи уравнений, когда стоит на первом месте, а -на втором (1 - вещественное уравнение, 2 - мнимое), откладывается на оси абсцисс, а - на оси ординат. В случае перемены местами осей соответственно меняется ориентация штриховки относительно правой и левой сторон на противоположную. Как и при D-разбиении в плоскости одного комплексного параметра, найденные заштрихованные претенденты на область устойчивости должны проверяться (область I: и , рис. рисунок 12.4 а). Для этого в каждой из областей претендентов на область устойчивости выбираются значения параметров и одним из известных критериев САУ проверяется на устойчивость. Если при выбранных параметрах САУ устойчива, то эта область и будет областью устойчивости. При применении метода D-разбиений необходимо строго соблюдать изложенные выше формальные процедуры.

 

Рассмотрим пример 1.

 

В работе рассматривается следящая система управления, предназначенная для воспроизведения входного сигнала. В следящей системе выходная величина воспроизводит изменение входной величины, причем автоматическое устройство реагирует на рассогласование между входной и выходной величинами. Система содержит последовательно включенные усилитель мощности УМ, объект управления ОУ и датчик обратной связи ДОС, связанный с ОУ при помощи кинематической связи КС .

Функциональная схема замкнутой системы с пропорциональным регулятором Р приведена на рисунке 12.5.

 

Рисунок 12.5 – Функциональная схема замкнутой системы

 

Усилитель мощности предполагается безынерционным, но с ограниченной зоной линейности при