Импульсная характеристика и передаточная функция

Многолучевой канал связи, как любая линейная система, определяется однозначно своей ИХ во временной области и/или передаточной функцией в частотной области. ИХ канала, и его передаточная функция позволяют определить связь выходного и входного сигналов и их спектров соответственно. Многолучевой канал показан на рис. 2.4.

Рис. 2.4. Многолучевой канал

В многолучевом канале сигнал распространяется по многим путям, и n-ый путь (луч) характеризуется задержкой сигнала t_n(t) и комплексным коэффициентом передачи a_n(t). Если передается сигнал s(t), то на входе приемника наблюдается сигнал x(t), представляющий собой сумму сигналов, распространяющихся различными путями. Этот сигнал можно записать следующим образом:

, (2.3.1)

Подавляющее большинство систем связи применяют узкополосные сигналы, которые могут быть представлены в виде (1.1.2). Подставив (1.1.2) в (2.3.1), получим, что

. (2.3.2)

Отсюда следует, что комплексная амплитуда принимаемого низкочастотного сигнала равна

. (2.3.3)

Далее будем предполагать, что за время прохождения сигнала задержки t_n(t) и комплексные коэффициенты передачи a_n(t) для всех лучей остаются неизменными и равными t_n и a_n.

По определению ИХ линейной системы с фиксированными параметрами является откликом системы на входной d-импульс. Поэтому ИХ канала мы получим, если подадим на вход канала сигнал (1.1.2) с комплексной амплитудой равной . В результате будем иметь, что

. (2.3.4)

Чтобы получить передаточную функцию канала , необходимо взять гармонический сигнал единичной амплитуды частоты f, т.е. подставить в (2.3.1) сигнал . Тогда получим, что

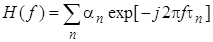. (2.3.5)

В качестве примера рассмотрим свойства двулучевого канала. Предположим, что имеется прямой сигнал и сигнал, отраженный местным предметом. Прямой сигнал приходит без искажения и имеет задержку на время распространения от передатчика до приемника. Кроме того, его амплитуда уменьшается и зависит от расстояния между передатчиком и приемником. Эти изменения параметров сигнала не имеют принципиального значения для нашего рассмотрения. Поэтому начало отсчета времени совместим с моментом прихода прямого сигнала в приемную антенну, а амплитуду прямого сигнала нормируем так, чтобы она была равна единице. Фазу прямого сигнала примем равной нулю. В этом случае из (2.3.4) получаем, что канал можно характеризовать ИХ

, (2.3.6)

где – комплексный коэффициент отражения сигнала от местного предмета, – разность фаз между первым и вторым сигналами из-за задержки t₂ второго сигнала относительно первого, а₂ – комплексная амплитуда второго сигнала по отношению к первому.

ИХ двулучевого канала изображена на рис. 2.5.

Рис. 2.5. Двулучевой канал: а) на вход приемника приходят прямой s₁ и отраженный s₂
сигналы; б) ИХ двулучевого канала

Заметим, что ИХ канала (2.3.6) не дает информации о направлении прихода второго сигнала. Обычно предполагается, что второй сигнал имеет меньшее значение амплитуды, т.е. .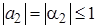

Передаточную функцию канала найдем из (2.3.5). Получим, что

. (2.3.7)

Коэффициент передачи канала по мощности определяется как квадрат модуля передаточной функции, т.е.

. (2.3.8)

Пример этой функции приведен на рис. 2.6 для |a₂|=0.8, t₂=1, arga₂=p/6. Видно, что коэффициент передачи канала по мощности имеет максимумы и минимумы, то есть гармонические сигналы с некоторыми частотами ослабляются, в то время как с другими частотами усиливаются. Минимумы наблюдаются для частот , где n=0, ±1,¼. Расстояние между минимумами на оси частот не зависит от фазы коэффициента отражения a₂ и равно . Средний коэффициент передачи по мощности равен 1+|a₂|² и показан на рис. 2.6 штриховой линией, минимум равен (1-|a₂|)², а максимум - (1+|a₂|)². Если амплитуда прямого сигнала равна амплитуде задержанного сигнала, то может наблюдаться полное пропадание сигнала на входе приемника.

Рис. 2.6. Коэффициент передачи двулучевого канала по мощности

Изменение уровня принимаемого сигнала, вызванное интерференцией сигналов, проходящих в канале различными путями, принято называть замираниями принимаемого сигнала или федингами. Если полоса пропускания приемника , то все спектральные компоненты сигнала в пределах частотной полосы приемника будут испытывать дружные замирания. В этом случае принято говорить, что канал является плоским (flat channel). Если выполняется другое условие , то различные спектральные компоненты сигнала испытывают различные замирания. В этом случае говорят, что канал является частотно селективным (frequency selective channel).

Фаза отраженного сигнала в (2.3.7) может изменяться значительно даже при очень малых изменениях задержки t₂ этого сигнала. В самом деле, изменение фазы на 2p радиан происходит при изменении задержки t₂ на 1/f. Например, если несущая частота f_c=900 МГц, то величина 1/f составляет всего 1,1 наносекунд, что соответствует изменению пути распространения сигнала на 33 см, то есть на длину волны. Таким образом, если разность хода между прямым и отраженным сигналами изменится всего на 16.5 см, разность фаз между ними изменится на 180 градусов. Этот пример показывает, что сигнал может испытывать глубокие и быстрые замирания даже при движении абонента со скоростью пешехода.