Пространственная корреляция

Предположим, что имеется две приемные антенны A1 и А2, расположенные на расстоянии d друг от друга. На рис. 2.23 показаны эти антенны, протяженный источник, угловые координаты j (азимут) и q (угол места), а также выделен элемент телесного угла dW равный .

Рис. 2.23. Расположение протяженного источника относительно двух антенн в системе
угловых координат j,q.

Диаграмму направленности антенны А1 зададим в виде комплексной функции . Если бы антенна А2 находилась в начале координат также как антенна А1, то она имела бы диаграмму направленности в виде некоторой другой функции . Поскольку антенна А2 смещена из начала координат, ее диаграмма направленности должна учитывать это смещение в виде дополнительного множителя, то есть она равна . Здесь учтено, что величина равна косинусу угла между осью x и направлением с координатами (j,q). Таким образом, диаграммы направленности обеих антенн могут быть представлены в единой системе координат.

Сигнал в каждой антенне представляет собой сумму элементарных сигналов протяженного источника. Поэтому комплексная амплитуда сигнала в каждой антенне может быть представлена в виде интеграла.

, (2.3.117)

. (2.3.118)

Здесь величина имеет смысл комплексной амплитуды плоской волны, приходящей с направления (j,q), интегрирование предполагается в пределах всей сферы, т.е. в пределах телесного угла, равного 4p.

Естественно предположить, что элементарные сигналы, приходящие из различных элементов протяженного источника, некоррелированы между собой. Математически это можно выразить следующей формулой:

, (2.3.119)

где функция имеет смысл плотности потока мощности, переносимой плоской волной с направления (j,q).

Поскольку нас интересуют эффекты, связанные только с угловой протяженностью (угловой дисперсией) источника сигнала, для функции будем использовать интегральную нормировку, при которой . Такая нормировка предполагает, что полная мощность источника является фиксированной.

Используя (2.3.117), (2.3.118) и (2.3.119), нетрудно найти среднюю мощность, принимаемую каждой антенной, и функцию корреляции сигналов, принятых антеннами А1 и А2. В результате будем иметь, что

, (2.3.120)

, (2.3.121)

. (2.3.122)

Отсюда найдем, что коэффициент корреляции сигналов, принятых антеннами, равен

. (2.3.122)

Выражение (2.3.122) существенно упрощается, если диаграммы направленности обеих антенн не зависят от угловых координат и могут быть заменены фиксированными значениями (изотропные излучатели). Тогда из (2.3.122) получим, что

. (2.3.123)

Рассмотрим некоторые частные случаи, которые помогают понять общие закономерности пространственной корреляции сигналов. Обозначим - расстояние между антеннами, выраженное в длинах волн.

1. Источник сигнала имеет пренебрежимо малые угловые размеры. В этом случае мы говорим об отсутствии угловой дисперсии сигнала. Допустим, что источник сигнала имеет угловые координаты (j₀,q₀). Тогда функция углового распределения мощности может быть представлена в виде d-функции, т.е. . В этом случае единственная плоская волна приходит с направления (j₀,q₀). Используя фильтрующее свойство d-функции, из (2.3.123) находим, что

. (2.3.124)

Модуль коэффициента корреляции равен единице, а его фаза меняется линейно в зависимости от расстояния d между антеннами.

2. Рассеиватели расположены равномерно по окружности в горизонтальной (азимутальной) плоскости, что соответствует рассмотренной выше модели Кларка. Тогда двумерная функция углового распределения мощности . В этом случае из (2.3.123) находим, что

. (2.3.125)

Функция Бесселя J₀(x) первого рода нулевого порядка имеет максимум, когда x=0. При увеличении аргумента x она спадает и достигает значения (1/e)»0,37 при x»1.75. Поэтому радиус корреляции будет составлять . Это значит, что принятые антеннами сигналы будут некоррелированными, если антенны разнести на расстояние ~0.5l. Конечно, здесь предполагается, что антенны не имеют электромагнитного взаимодействия. В противном случае сигналы будут коррелированны из-за электромагнитного взаимодействия антенн [41].

Формула (2.3.125) следует также из выражения (2.3.91) для функции автокорреляции. Для этого в (2.3.91) необходимо время задержки t преобразовать в пространственное смещение d посредством очевидного соотношения .

3. Рассеиватели расположены в горизонтальной плоскости и сосредоточены вблизи азимутального угла j=0.5p, который соответствует направлению нормали к линии, соединяющей антенны. При этом можно сделать следующую замену переменных j=0.5p-x. В этом случае cosj=sinx»x. Тогда функцию углового распределения мощности следует представить в виде . В этом случае из (2.3.123) находим, что

. (2.3.126)

Отсюда заключаем, что угловое распределение мощности источника и пространственный коэффициент корреляции связаны между собой преобразованием Фурье.

4. Некоторые канальные модели (например, так называемая 3GPP модель [49]) предполагают, что функция углового распределения мощности дается функцией Лапласа в виде

, (2.3.127)

где D - угловой размер источника на уровне -3дБ.

Подставляя (2.3.127) в (2.3.126), найдем, что

. (2.3.128)

На рис. 2.24 показан коэффициент корреляции (2.3.128) в зависимости от u=d/l для источника с угловым размером 2°, 5° и 8°.

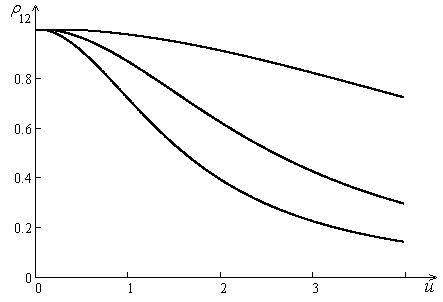
Рис. 2.24. Коэффициент корреляции для лапласовского источника с угловым размером 2°,
5° и 8° (кривые 1, 2 и 3, соответственно).

Видно, что для источников с большей угловой дисперсией коэффициент пространственной корреляции уменьшается с расстоянием в большей степени.

5. Предположим, что функция углового распределения мощности дается функцией Лапласа в виде

, (2.3.129)

где угловое направление на центр источника равно x₀.

Предположим также, что угол x₀ является случайной величиной с плотностью вероятности p(x₀). В частности, 3GPP канальная модель предполагает, что случайная величина x₀ имеет нормальное распределение. Чтобы вычислить коэффициент корреляции, необходимо сделать в (2.3.126) дополнительное усреднение по случайному параметру x₀. В результате получим, что

. (2.3.130)

Интеграл в этом выражении представляет собой характеристическую функцию для плотности вероятности p(x₀).

6. Если предполагается гауссовская функция (2.3.114) углового распределения мощности, то из (2.3.126) будем иметь (обозначая )

. (2.3.131)

Интеграл (2.3.131) вычисляется. В результате будем иметь, что

. (2.3.132)

Первый множитель определяет осциллирующий характер коэффициента корреляции и соответствует полученному ранее выражению (2.3.124). Второй множитель определяет спадающий характер коэффициента корреляции, обусловленный угловым рассеянием в канале. Принимая x₀=0, получим, что радиус корреляции по уровню 1/e будет составлять , то есть он уменьшается с увеличением углового размера источника. Например, при x_eff=10° получим, что , то есть в »6.5 раз больше соответствующей величины для модели Кларка.

Как уже отмечалось выше, в городских условиях пользователь принимает сигналы БС, рассеянные окружающими его отражателями, со всех направлений, то есть для пользователя БС представляется протяженным источником с угловым размером равным 2p. Базовая станция принимает сигналы пользователя в некоторой угловой области шириной 2q_eff (по уровню 1/e). Таким образом, радиус корреляции сигналов в антеннах пользователя меньше половины длины волны, а радиус корреляции сигналов в антеннах БС обычно значительно больше и может составлять несколько длин волн.