Вероятность битовой ошибки в райсовском канале

Рассмотрим вероятность битовой ошибки для сигналов бинарной фазовой модуляции. В случае райсовких замираний сигнала коэффициент передачи h можно представить как сумму коэффициентов передачи регулярной (статической) h^(st) и случайной h^(Rl) (релеевской) компонент: 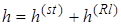. Фаза коэффициента h^(Rl) равновероятна в пределах [0¸2p], а реальная и мнимая части имеют гауссовское распределение с нулевым средним и с суммарной дисперсией раной единице.

Учитывая (2.4.1), получим, что выходной сигнал равен

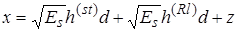. (2.5.1)

Первое слагаемое описывает не флуктуирующую (статическую) составляющую, средняя мощность которой в 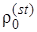раз больше мощности собственного шума. Второе слагаемое h^(Rl) представляет собой случайную (релеевскую) составляющую с нулевым средним и дисперсией в 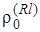раз больше мощности собственного шума.

В многолучевом райсовском канале амплитуда |h| коэффициента передачи имеет райсовское распределение вида (2.3.54). При этом случайное ОСШ r будет иметь плотность вероятности с параметром 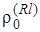, которую можно записать как

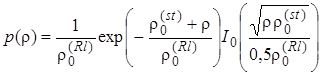. (2.5.2)

Чтобы найти вероятность битовой ошибки в райсовском канале подставим функцию p(r) из (2.5.2) в (2.4.4). В результате получим, что

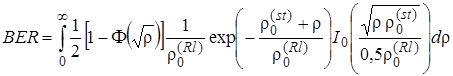. (2.5.3)

Это выражение является достаточно сложным. Однако его можно упростить [23]. В соответствии с ([43] № 8.252-4) интеграл вероятности в (1.3.11) представим в виде

, (2.5.4)

где Re(y²)>0.

Подставляя в (2.5.4) x=1 и 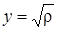получим, что

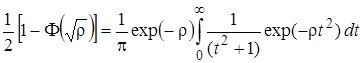. (2.5.5)

С помощью (2.5.3) и (2.5.5) придем к следующему выражению для вероятности битовой ошибки:

, (2.5.6)

Учитывая (2.5.2), получим, что внутренний интеграл в (2.5.6) равен [23]

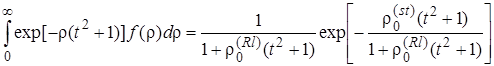. (2.5.7)

Теперь с помощью (2.5.6) и (2.5.7), найдем, что

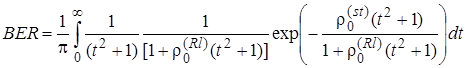. (2.5.8)

Выражение (2.5.8) значительно более простое, чем (2.5.3). В самом деле, в (2.5.3) вероятность битовой ошибки определяется через интеграл от интеграла вероятности F(x) и функции Бесселя I(x) мнимого аргумента нулевого порядка, которая, в свою очередь, также имеет интегральное представление. В то же время в (2.5.8) вероятность ошибки определяется через однократный интеграл по действительной переменной от произведения достаточно простых функций.

Часто более удобным является представление вероятности ошибки через среднее ОСШ r₀ и отношение мощностей стационарной и релеевской компонент (K-фактор). Тогда, учитывая формулы (2.3.58) перехода, вместо (2.5.8) будем иметь

. (2.5.9)

Если релеевская составляющая замираний сигналов значительно превышает собственный шум ( 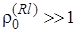), то интеграл (2.5.9) вычисляется и вероятность ошибки будет равна

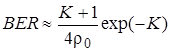. (2.5.10)

Когда статическая составляющая сигнала отсутствует ( K=0) из (2.5.9) следует формула (2.4.6) для вероятности битовой ошибки в релеевском канале. В самом деле, при K=0 выражение (2.5.9) приобретает вид

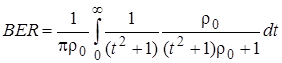. (2.5.11)

Этот интеграл представим в виде разности двух интегралов:

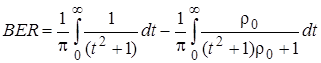(2.5.12)

Оба интеграла являются табличными и вычисляются. В результате получим

, (2.5.13)

что совпадает с (2.4.6). Нетрудно также получить (2.4.7) из (2.5.10).

На рис. 2.27 показана вероятность битовой ошибки в райсовском канале в зависимости от среднего ОСШ r₀ для разных значений K-фактора. Видно, что при одинаковом ОСШ вероятность ошибки уменьшается c увеличением K, то есть с уменьшением релеевской составляющей флуктуации сигналов.

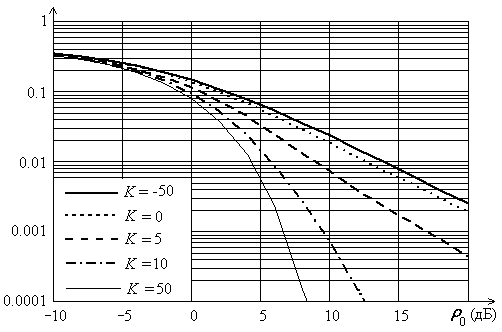
Рис. 2.27. Вероятность битовой ошибки в райсовском канале в зависимости от ОСШ r₀ для
K= -50, 0, 5, 10 и 50 дБ

С помощью (2.5.8) можно получить нижнюю и верхнюю границы для вероятности ошибки в райсовском канале. Умножим и разделим аргумент экспоненты на относительную дисперсию 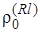флуктуаций коэффициента передачи и учтем, что на всем интервале [0¸¥] интегрирования по переменной t в (2.5.8) имеет место условие вида

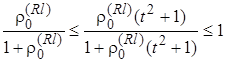. (2.5.14)

Отсюда следует, что вероятность битовой ошибки BER^(Rc) в райсовском канале заключена в следующих пределах:

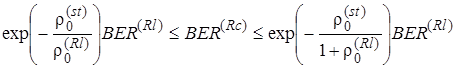, (2.5.15)

где BER^(Rl) - вероятности ошибки в релеевском канале.

Интересный вид имеет графики на рис. 2.28 для вероятности битовой ошибки в райсовском канале в зависимости от дисперсии 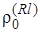релеевских замираний сигнала, при разных амплитудах a регулярной составляющей сигнала. Обращает на себя внимание вид кривых при a>0. Сначала вероятность ошибки увеличивается с ростом 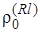, хотя полная средняя мощность принятого сигнала при этом возрастает. После достижения максимума вероятность ошибки начинает уменьшаться и приближается к вероятности, соответствующей релеевскому каналу.

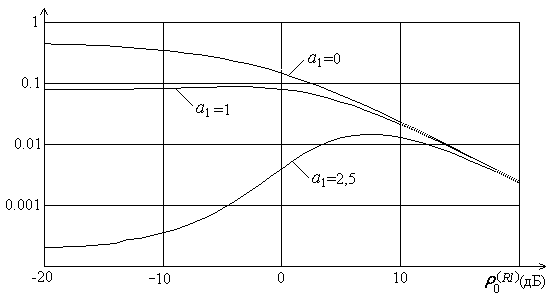
Рис. 2.28. Вероятность битовой ошибки в райсовском канале в зависимости от дисперсии
релеевских замираний для разных амплитуд регулярной составляющей сигнала

Глава 3. Основные характеристики систем
с разнесенным приемом

В литературе, посвященной обработке сигналов в сотовых системах связи, прием сигнала с помощью N антенн часто обобщают, имея в виду N ветвей разнесения [4,5]. При этом под каждой ветвью понимают либо одну из приемных антенн (рис. 3.1 слева), либо один из задержанных лучей, приходящих на единственную антенну (рис. 3.1 справа). В первом случае принятые разными антеннами сигналы суммируются с некоторыми весовыми коэффициентами. Во втором случае используется так называемый RAKE-приемник, который обеспечивает выравнивание по времени задержанных сигналов, и затем их когерентное суммирование [4,5]. Отметим, что устройство, обеспечивающее когерентное суммирование приемных антенн, было предложено в [50].

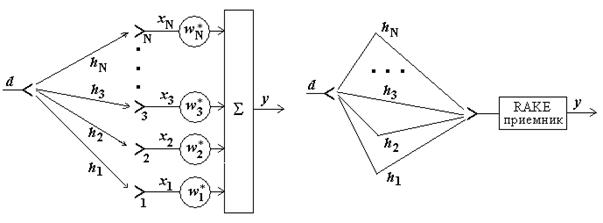
Рис. 3.1. Разнесенный прием сигналов

В любом случае свойства пространственного канала определяются вектором-столбцом ((.)^T – знак транспонирования) коэффициентов передачи для каждой приемной антенны или для каждого луча. Более того, с математической точки зрения эти две системы эквивалентны друг другу.

В данной главе мы будем рассматривать прием сигналов N-элементной АР (пространственный разнесенный прием). Особенности временной обработки сигналов в RAKE-приемнике будут рассмотрены ниже.