 |
Главная |
Работа внутренних сил упругой стержневой системы
|
из
5.00
|
Работа внешних сил на соответствующих им перемещениях может быть выражена и через внутренние силы, вызываемые ими. Выделим из стержня двумя сечениями, перпендикулярными к его оси, бесконечно малый элемент длиной dS,на который могут действовать следующие системы плоских сил: продольная N, поперечная Q и изгибающий момент М (рис.32, а). Если усилия N, Q и M по отношению к целому стержню являются внешними, вызывающими деформации элемента длиной dS, то по отношению к выделенному элементу они внутренние. Внутренние силы направлены в сторону, противоположную деформации, и сопротивляются ей, и поэтому суммарная работа внутренних сил будет отрицательной. Например, если стержень растянут (рис.32,б), то в сечениях а-б будут действовать две равные и противоположно направленные силы N. Одни из них будут растягивать элемент длиной dS, а другие, называемые внутренними, будут препятствовать деформации элемента dS. Рассмотрим отдельно влияния каждого из этих усилий на элемент длиной dS.
Под действием статического приложенного внешнего усилия N (рис.32,в), равномерно распределенного по сечению, удлинение  элемента ds будет равно
элемента ds будет равно  , где F – площадь поперечного сечения стержня. Поскольку сила нарастает постепенно от нуля до полного значения N, работа внутренних сил
, где F – площадь поперечного сечения стержня. Поскольку сила нарастает постепенно от нуля до полного значения N, работа внутренних сил
 (60)
(60)
|

| |||
| |||
При действии на элемент dS внешних изгибающих моментов М (рис.32, г), приложенных по торцам, оба сечения поворачиваются друг относительно друга на бесконечно малый угол  . Так как
. Так как 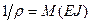 и
и 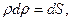 то
то  . Под действием статически возрастающего момента M на этом угловом перемещении будет совершена работа внутренних сил
. Под действием статически возрастающего момента M на этом угловом перемещении будет совершена работа внутренних сил
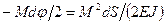 (61)
(61)
Элемент dS, находящийся под действием поперечных сил Q, показан на рис.32, д и е. На рис.32, д представлен суммарный линейный сдвиг соответствующих элементарных полосок на обоих торцах элемента dS. Суммарные линейное перемещение элементарных полосок составит  , где b – ширина сечения элемента в исследуемом уровне; S – статический момент относительно нейтральной оси той части сечения, которая расположена выше выделенной полоски; J-момент инерции всего поперечного сечения относительно нейтральной оси.
, где b – ширина сечения элемента в исследуемом уровне; S – статический момент относительно нейтральной оси той части сечения, которая расположена выше выделенной полоски; J-момент инерции всего поперечного сечения относительно нейтральной оси.
Внутреннее усилие, соответствующее части поперечного сечения выделенного элемента на заштрихованной элементарной площадке (рис.32, е), равно  . Работа бесконечно малой касательной силы τdF при ее постепенном возрастании на перемещении
. Работа бесконечно малой касательной силы τdF при ее постепенном возрастании на перемещении  выразится произведением
выразится произведением  .Интегрируя в пределах всего поперечного сечения F, получил элементарную работу поперечных сил.
.Интегрируя в пределах всего поперечного сечения F, получил элементарную работу поперечных сил.
Для того чтобы получить полную работу внутренних сил, необходимо просуммировать элементарные работы в пределах всего стержня и по всем стержням плоской стержневой системы.
Получим следующее выражение для полной работы внутренних сил:
 (62)
(62)
Поскольку работа внутренних сил А равна по абсолютной величине, но противоположна по знаку работе внешних сил W и потенциальной энергии деформации упругого тела U, то
W = – A = U (63)
Для плоской стержневой системы потенциальная энергия выражается следующей формулой:  (64)
(64)
|
из
5.00
|
Обсуждение в статье: Работа внутренних сил упругой стержневой системы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


