Формула Мора для определения перемещений

Определение перемещений точек (или узлов) стержневых систем необходимо для установления деформативности конструкций и решения статически неопределимых задач.

Вывод формулы перемещений основывается на общей теореме о взаимности работ или на равенстве возможных работ внешних и внутренних сил .

Состояние этой системы называют действительным или грузовым (в случае силового воздействия). Будем обозначать его индексами m (в общем случае) или p,t и d, b зависимости от вида воздействия. Для этой же системы выберем другое, вспомогательное R-ое состояние, в котором действует одна обобщенная единичная сила , не имеющая размерности (рис.38,б). Это состояние называют фиктивным или единичным. В соответствии с выражениями или составим для плоской системы следующее равенство:

(79)

Отбрасывал в левой части безразмерную силу , получим так называемую формулу Мора – формулу определения перемещений для плоских стержневых систем от действия нагрузки в действительном состоянии в месте приложения силы по направлению этой силы: , (80)

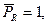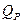где и – внутренние усилия в системе от силы приложенной по направлению искомого перемещения; и – внутренние усилия от заданной нагрузки.

Для пространственных стержневых систем формула Мора аналично формуле (72) состоит из шести членов:

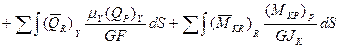(81)

При применении формулы Мора обычно отбрасывают члены, влиянием которых на перемещение можно пренебречь. Так, например, при определении перемещений узлов как плоских, так и пространственных ферм (шарнирно-стержневых систем) используют только первый член формулы Мора:

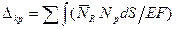(82)

При расчете плоских балок и рам обычно учитывают только деформации изгиба:

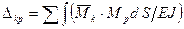(83)

Отметим, что если система состоит из коротких стержней , то пренебрегать деформациями сдвига нельзя. Применение формулы Мора существенно упрощается, если интегрирование производить по правилу Верещагина, которое заключается в следующем. Интеграл типа , в котором одна из функций на интервале интегрирования изменяется по линейному закону (например, ), может быть определен произведением площади эпюры первой функции Ώ на координату под ее центром тяжести, взятую со второй эпюры (рис. 39), то есть (84)

При «перемножении» эпюр следует учитывать их знаки. Если стержни криволинейны или их жесткости на участках интегрирования не постоянны, перемещения следует определять методом непосредственного интегрирования. В таблице 1 приведены некоторые формулы, полученные в результате интегрирования грузовых эпюр с линейной единичной эпюрой .

«Треугольные» или «прямоугольные» единичные эпюры могут рассматриваться как частные случаи эпюры . В двух последних эпюрах моменты изменяются по закону квадратной параболы.

Таблица 1