Механизмы собственного поглощения

В случае, когда поглощение кванта оптического излучения полупроводником приводит к переходу электронов из валентной зоны в зону проводимости, то такое поглощение называют собственным или фундаментальным.

Как отмечалось выше, коэффициент поглощения αявляется функцией концентрации поглощающих центров, частоты (длины волны) света, и свойств полупроводника. Концентрация поглощающих центров является определяющим фактором поглощения света полупроводником. Поскольку концентрация атомов основного материала превалирует в любом практически важном полупроводнике, поэтому собственное поглощение (поглощение света с переходом зона-зона) является наиболее важным среди всех остальных видов поглощения.

В настоящих лекциях подробно рассмотрим механизмы собственного поглощения. В частных случаях прямых и непрямых переходов или при различных механизмах рассеяния носителей заряда при по­глощении свободными носителями зависимости α(hν) имеют существенно различ­ный вид. В частности, характер спектральной зависимости ко­эффициента поглощения определяется двумя факторами: зависимостью плотности состояний от энергии в обеих разрешенных зонах и зависи­мостью вероятности перехода W. В квантово-механической теории пе­реходов выводится выражение для α(Е), имеющее вид:

(4.8)

где А - коэффициент пропорциональности; - сила осциллятора для перехода из состояния с волновым вектором k_i в валентной зоне в состояние с волновым вектором k_f в зоне проводимости; N_if(Е) - комбинированная плот­ность состояний, участвующих в оптическом переходе. В свою очередь, сила осциллятора является величиной, пропор­циональной вероятности перехода:

~ W²(k) (4.9)

Дальнейший анализ сводится к рассмотрению энергетических за­висимостей величин, входящих в (4.8) для оптических переходов разного типа.

Рассмотрим функциональные зависимости собственного (фундаментального) поглоще­ния света в случае прямых и непрямых переходов.

4.2.1. Прямые переходы.

Пусть электрон, из начального состояния в ва­лентной зоне с волновой функцией 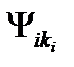поглотив квант света, перехо­дит в состояние с волновой функцией в зоне проводимости. Будем считать импульс фотона k_ph значительно меньшим импульса электрона в начальном и конечном состояниях:

k_ph << k_i, k_j, (4.10)

Тогда закон сохране­ния импульса при прямом переходе приобретает вид

k_i = k_j, (4.11)

Полное число прямых переходов получается суммированием по всем состояниям, для которых справедлив закон сохранения энергии с уче­том зависимости вероятности перехода от энергии. Очевидно, что при любой зависимости Е от k в начальной и конечной зонах каждому со­стоянию в валентной зоне с данным значением вектора k_i соответствует только одно состояние в зоне проводимости с тем же значением векто­ра k_f= k_i. Таким образом, энергии электрона в начальной зоне Е_i и в ко­нечной зоне Е_f однозначно определяются энергией фотона. В простей­шем частном случае изотропных зон с квадратичным законом диспер­сии (Е ~ k²) при данной энергии фотона в процессе прямых переходов прини­мают участие только состояния, расположенные на сферах с энерги­ями:

и , (4.12)

где m*_i и m*_f – эффективные массы плотности состояний начальной и конечной зон; а

E = hν – E_g (4.13)

Схема энергетических поверхностей в пространстве, иллюстрирую­щих прямые переходы, приведена на рис. 4.5. Плотность состояний в валентной зоне в интервале энергий от Е_iдо Е_i + dE_iбез учета спина по аналогии с (2.11)

(4.14)

Из рис. 4.5 видно, что именно эта плотность состояний участвует в прямых переходах при энергиях фотонов, заключенных в интервале hν ÷ h(ν+dν). Поэтому, комбинируя (4.12) и (4.14), мож­но представить плотность состояний N_if(Е) в виде:

, (4.15)

где Е определено выражением (4.13). Таким образом, входящий в (4.8) сомножитель N_if(Е) связан с энергией фотона hv квадратичной зависимостью: N_if(Е) ~ (hv)^1/2

 

Рис. 4.5. Схема энергетиче­ских поверхностей в E-k координатах, иллюстрирующая прямые переходы.	Рис. 4.6. Зависимость E(k) для трех соседних зон, образованных из s-, p- и d-состояний атомов решетки.

 

Для анализа энергетической зависимо­сти вероятности прямого перехода W(k) разло­жим ее в ряд в окрестности значений k₀:

(4.16)

Вероятность перехода электрона из валентной зоны в зону проводимости сильно зависит от симметрии и четности волновых функций электронов в этих зонах. Если четность волновых функций одна и та же (например, валентная зона получена на основе s-состояний, а зона проводимости – на основе d-состояний (рис. 4.6)), тогда вероятность перехода в точке k=0 равна нулю (т.е. W(k₀) =0; хотя для всех k≠0, вероятность W(k) не равна нулю). Если же волновые функции обладают различной четностью (например, валентная зона получена на основе s-состояний, а зона проводимости – на основе p-состояний (рис. 4.6)), тогда вероятность перехода в точке k=0 отлична от нуля (т.е. W(k₀)≠ 0). В зависимости от этого различают «разрешенные» или «запрещенные» переходы.

Оптические переходы являются разрешенными, если зоны, между которыми происходит переход электронов, образованы из состояний, для которых орбитальные квантовые числа различаются на единицу, а волновые функции электронов в этих зонах имеют различную четность. Например, разрешенным является переход между валентной зоной, образованной из s-состояния, и зоной проводимости, образованной из p-состояния.

Оптические переходы являются запрещенными, если зоны, между которыми происходит переход электронов, образованы из состояний, для которых орбитальные квантовые числа различаются на 0 или 2 единицы, а волновые функции электронов в этих зонах имеют одинаковую четность. Например, запрещенными является переход между валентной зоной, образованной из s-состояния, и зоной проводимости, образованной из d-состояния.

Из вышеизложенного следует, что для разрешенных прямых переходов W(k₀)≠ 0, тогда как для запрещенных переходов – W(k₀) =0. Следовательно, для разрешенных переходов в выражении (4.16) можно ограничиться первым членом. Тогда сила осциллятора будет постоянной величиной, не зависящей от энергии Е = hv. Для запрещенных переходов первое слагаемое в (4.16) обращается в ноль, а при подстановке второго слагаемого в (4.9) получаем:

~ k² ~ E (4.17)

Подставив полученные энергетические зависимости величин N_if (4.15) и (4.16 или 4.17) в (4.8), заменив Е на hv (4.13) найдем спектральные характе­ристики коэффициента поглощения в случаях прямых разрешенных и прямых запрещенных переходов соответственно:

α(hν) = A·(hν)^1/2 (4.18)

α(hν) = B·(hν)^3/2 (4.19)

Эти выражения справедливы для параболичных зон. Отклонение отпараболичности начальной и конечной зон может быть учтено введе­нием в (4.12) и соответственно в (4.15) эффективных масс, зависящих от энергии.

В сильно легирован­ных (вырожденных) полупроводниках, состояния вблизи экстремума соответствующей зоны могут оказаться заполненными носителями заряда. В этом случае край поглощения сдвигается в сторону больших энергий. Этот эффект носит название «бурштейновский сдвиг». При сильном легировании возможен и другой эффект - сужение запрешенной зоны за счет слияния при­месной зоны с краем ближайшей разрещенной зоны. Если этот эффект значителен, то край поглощения может сдвигаться в сторону меньших энер­гий.

 

4.2.2. Непрямые переходы.

Схема, иллюстрирующая непрямые переходы, показана на рис. 4.7. Переход из начального состояния i в валентной зоне в ко­нечное состояние f в зоне проводимости можно рассмат­ривать как двухступенчатый процесс: элек­трон с импульсом ħk_i, близким к нулю, под действием света с энергией hv совер­шает прямой переход в виртуальное состояние α, расположенное в центральной долине зоны проводимости, а затем рассеи­вается каким-либо центром рассеяния (наиболее часто – фононом) и переходит в конечное состояние f с им­пульсом ħk_f .

Рис. 4.7. Схема энергетиче­ских зон, поясняющая про­цесс непрямого перехода i­ à f с участием промежуточно­го состояния а. Во многих случаях удобно рассматривать реальный процесс как последовательную сумму нескольких других процессов. При этом все про­межуточные процессы, хотя и не существуют реально, но с их введением появляется возможность либо лучше понять действительный про­цесс, либо описать его количественно. Такие промежуточные процессы носят название виртуальных. Соответственно промежуточные состояния частиц называют виртуальными состояниями.

 

Время нахождения электрона в виртуальном состоянии ничтожно мало, поэтому для всего перехода в целом имеет место сохранение энергии. Полная вероятность непрямого перехода W_t определяется уже извест­ной нам вероятностью прямого перехода W и вероятностью рассеяния электрона W_s. Поскольку основным механизмом рассеяния носителей при комнатной температуре является рассеяние на квантах колебания решетки (на фононах), непрямой переход является переходом с участием как минимум трех физических тел – электрона, фотона и фонона. Таким образом, непрямые или невертикальные переходы осуществляются с испусканием или с поглощением фононов.

Теоретическое рассмотрение составляющих процессов непрямого перехода дает соотношение:

, (4.20)

где E_g0- ширина запрещенной зоны в точке k= 0; Е_а, E_g, Е_f показаны на рис. 4.7.

Если предположить, что W_s не зависит от частоты фотона, то энергети­ческая зависимость полной вероятности непрямого перехода будет определяться, лишь знаменателем в (4.20) и энергетической зависимо­стью вероятности прямого перехода W(Е), которая появляется, как было показано, для запрещенных переходов.

Если для полупроводника выполняется неравенство

E_go - E_g >> Е_а, Е_f (4.21)

(это, например, имеет место в кремнии), то знаменатель в (4.20) мож­но положить равным E_go - E_g и, следовательно,

W_t = const·W (4.22)

Для определения коэффициента поглощения α(hv) снова используем выражение (4.8) с учетом (4.9). Тогда для невырожденного полупроводника в случае непрямых разрешенных переходов после подстановки N_if ~E² и W = const получаем:

α(hν) = C·(hν)² (4.23)

В случае непрямыхзапрещенных переходов в (4.8) подставляем (4.17) при том же N_if ~E². В результате получим:

α(hν) = D·(hν)³ (4.24)

где С и D - коэффициенты пропорциональности. Сопоставление значений а (hv) для прямых и непрямых переходов показывает, что в случае прямых переходов полупроводники поглощают свет значительно сильнее. (рис. 4.8). Это легко объяснимо, поскольку вероятность процесса, про­исходящего с двумя частицами (электрон и фотон), больше, чем с тре­мя частицами (электрон, фотон, фонон).

Рис. 4.8. Спектр поглощения оптического излучения чистыми кристаллами Ge, Si и GaAs.