Равновесные и неравновесные носители заряда. Квазиуровни Ферми

В идеальном собственном полупроводнике при температуре абсолютного нуля и при отсутствии иных источников энергии (фотонов, радиации и др.) в зоне проводимости нет электронов, а в валентной зоне - нет дырок. В этом случае электроны внешних оболочек связаны ковалентными связями и локализованы в валентной зоне, а электроны внутренних электронных оболочек находятся в более глубоких энергетических зонах. Поэтому свободных носителей заряда не существует и полупроводник не проводит электрический ток, т.е. является диэлектриком.

Однако, уже при незначительном увеличении температуры, за счет локальных термических флуктуаций, появляется ненулевая вероятность перехода электронов с донорных уровней или из валентной зоны в зону проводимости (образуются свободные электроны), а также электронов из валентной зоны на акцепторные уровни (образуются свободные квазичастицы – дырки). Процесс превращения связанного электрона в свободный носитель заряда (электрон или дырку) или в электрон-дырочную пару называется процессом генерации. На рис. 5.1 стрелками показаны переходы электронов при тепловом возбуждении и при наличии донорных и акцепторных уровней. Свободные носители зарядов, возникающие в результате тепловой генерации и находящиеся в термодинамическом равновесии с кристаллической решеткой, называют равновесными. В дальнейшем, для обозначения равновесных носителей заряда (электронов и дырок) будем использовать индекс «нуль»: n₀ и p₀.

Рис. 5.1. Тепловая генерация свободных носителей заряда и их концентрация в состоянии термодинамического равновесия. (а) и (б) - Генерация свободных электронов за счет ионизации собственных атомов (а) или ионизации донорных уровней (б). (в) – Генерация дырок за счет ионизации акцепторных уровней.   На рис. 5.1 изображены плотность квантовых состояний N(Е) в зоне проводимости и валентной зоне, функ­ция распределения Ферми-Дирака F(Е), а также концентрация равновесных электронов n0 и дырок p0, которые за­нимают состояния вблизи краев соот­ветствующих зон (заштрихованные области).

Одновременно с генерацией свобод­ных носителей заряда идет процесс рекомбинации: электроны возвращаются в незанятые состояния в валентной зоне или на уровни в запрещенной, в результате чего исчезают свободный электрон и свободная дырка. Т.е. рекомбинация это процесс превращения свободных носителей заряда (электронов, дырок или их пар) в связанное состояние.В усло­виях термодинамического равновесия процессы генерации и рекомбинации взаимно уравновешиваются. Обозначим через G₀ число генерируемых, а через R₀ - число рекомбинирующих электронно-дырочных пар в единице объема кристалла за одну секунду. Тогда равновесие процессов генерации и рекомбинации можно выразить следующей формулой химической реакции:

(5.1)

Функция G₀ в общем случае неизвестна, но в условиях термодинамического равновесия G₀=R₀. В свою очередь вероятность реком­бинации пропорциональна произведению концентраций свободных носителей заряда, поэтому:

R₀= γ_rn₀p₀, (5.2)

где γ_r - коэффициент пропорциональности, называемый коэффициентом рекомбинации

Помимо тепловой генерации, возникновение свободных носителей заряда может быть следствием других механизмов. Например, свободные носители могут образоваться в результате облучения полупроводника светом, разрыва валентных связей в сильных электрических полях или инжекции с помощью р-n перехода. Во всех этих случаях воз­никает некоторая концентрация электронов n и дырок р, которая отличается от термодинамически равновесной. Подвижные носители заряда, не находящиеся в термодинамическом равновесии как по кон­центрации, так и по энергетическому распределению, являются неравновесными носителями заряда, а их концентрацию n, р назы­вают неравновесной. Избыток неравновесной концентрации носи­телей заряда Δn, Δр в полупроводнике по сравнению с равновесной концентрацией n₀, p₀ принято называть избыточной концентрацией носителей заряда.

Очевидно, что подобно равновесному случаю, число неравновесных носителей заряда, возбуждае­мых светом (или каким-либо другим способом), не может расти до бес­конечности. Этому препятствуют процессы рекомбинации: чем больше сгенерировано свободных электронов и ды­рок, тем чаще оказываются их встречи друг с другом, т. е. тем вероят­нее их рекомбинация. После прохождения некоторого характерного времени система снова придет в равновесное состояние и это равновесие процессов генерации и рекомбинации можно выразить следующей формулой:

(5.3)

где R= γ_r∙n∙p; п = п₀+Δп; p = p₀+Δp.

При неравновесной генерации, в момент своего возникновения, носители заряда могут приобретать кине­тическую энергию, значительно превышающую среднюю тепловую энергию равновесных частиц. Например, если электрон валентной зоны получает энергию фотона hν>E_g, то переходя в зону проводимости он имеет кинетическую энергию Е= hν-E_g. Поэтому, на первый взгляд, можно предположить, что энергетическое распределение неравновесных и равновесных электронов сильно отличается. Однако в результате рассеяния на дефектах кристаллической решетки носители заряда довольно быстро пере­дают ей свою избыточную кинетическую энергию. Так, в типичном случае, передача энергии от неравновесного электрона к акустическим фононам происходит за ~ 100 столкновений. Так как среднее время между двумя столкновениями t ~ 10^-14 – 10^-13 c, то через 10^-12 – 10^-11 с, избыточные электроны приобретут температуру кристаллической решетки (иногда говорят, что «произойдет их термализация»). Поэтому в большинстве практически важных случаев распределение по энергиям неравновесных и равновесных носителей заряда можно считать одинаковым. Так, например, предельная частота переключения режимов работы биполярного транзистора – несколько гигагерц; следовательно, за время переключения (около 10^-9 с) термализация осуществляется с заведомо большим запасом по времени.

Процесс термализации сводится к тому, что неравновесные электроны, рассеивая свою избыточную энергию, как бы «опу­скаются» к нижнему краю зоны проводимости, а неравновесные дырки, рассеивая избыточную энергию, «поднимаются» к верхнему краю валентной зоны. Если при этом концентрация неравновесных носителей заряда мало отличается от равновесной, то передача кристаллу кинетической энергии неравновесными носителями заряда практически не изменит энергию решетки, а следовательно, и тем­пературу кристалла, поэтому не изменится концентрация равновес­ных носителей заряда. В связи с вышеизложенным, стационарную концентрацию неравновесных электронов п можно выразить с помощью формулы, аналогичной (2.49):

(5.4)

где 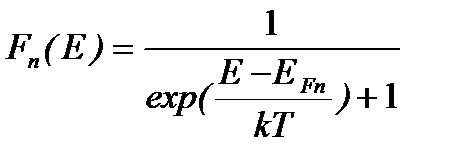- вероятность нахождения электрона на уровне энергии Е в зоне проводимости. Поскольку F_n(E) по форме совпадает с распределением Ферми-Дирака, то по определению E_Fnесть квазиуровень Ферми для электронов. В соответствии с (2.60) неравновесная концен­трация электронов в невырожденном полупроводнике:

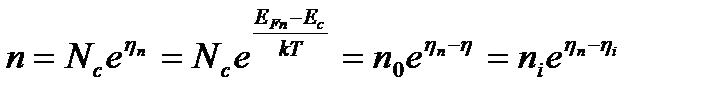(5.5)

где - приведенный квазиуровень Ферми для электронов.

- приведенный уровеньФерми для электронов в невырожденном полупроводнике в случае равновесной (термической) генерации.

- приведенный уровень Ферми для электронов в собственном полупроводнике, E_Fi=E_g/2.

Аналогично, концентрацию неравновесных дырок можно выра­зить следующим образом:

(5.6)

где - приведенный квазиуровень Ферми для дырок.

Таким образом, в неравновесном состоянии уровень Ферми как бы расщепляется на два квазиуровня - для электронов E_Fn и для дырок E_Fp, каждый из которых смещен по направлению к своей зоне на энергетическое расстояние, соответствующее относительной прибавке количества носителей (рис. 5.2).

Рис. 5.2. Расщепление уровня Ферми E_F на два квазиуровня - для электронов E_Fn и для дырок E_Fp. а - равновесное состояние; б - неравновесное состояние

Если теперь перемножить концентрации неравновесных носителей, то получим, что произведение концентраций электронов и дырок для неравно­весного состояния отличается от его значения для равновес­ного состояния:

или (5.7)

Это соотношение выражает связь между концентрациями элек­тронов и дырок в неравновесном состоянии. Расстояние между приведенными квазиуровнями Ферми (η_n-η_p) характеризует отклонение системы от состояния термодинамиче­ского равновесия. А именно – чем сильнее различаются квазиуровни Ферми электронов и дырок, тем сильнее отличается произведение концентраций неравновесных носителей заряда от произведения равновесных концентраций.