RISK : STRUCTURAL AND SOCIAL

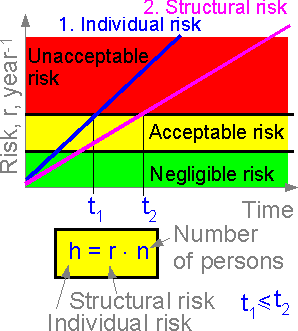Structural risk is connected with individual and social risks. Individual risk is equal to structural risk times the number of structural elements and number of people at risk.

The figure shows the structural and individual risks for a space shuttle. The individual risk of the crew member is the most important consideration, service with unacceptable individual risk (t > t₁) cannot be recommended. The more crew members, the higher the individual risk.

If an oil pipeline passes near a settlement the structural risk for L kilometers of the pipeline is equal to L times the structural risk of one kilometer. The more people in the settlement, the bigger the individual risk.

The structural risk of a severe accident of a structure can increase with time. If the risk exceeds the allowable value from corresponding industry standards the management of long-time service should be considered.

Another situation where a unique engineering structure is assessed for safety and improvements were made in the structural elements. There are no severe accidents. Safety assessments, knowledge of the likelihood of failure scenarios, and the design improvement can decrease risk. The more knowledge the smaller the risk.

The human factor plays a significant role. Nuclear power stations have backup systems and special nondestructive testing and inspections that decrease the risk.

Statistics can help choose a profession with lowest risk. Fortunately, other factors such as salary and interest also affect the decision.

Losses due to natural catastrophes such as tornadoes, earthquakes, forest fire, etc. at level 10¹⁰ are more valuable. More losses are connected with natural catastrophes than technical disasters.

REFERENCES

Hahn G.J.,Shapiro S.S. Statistical Models in Engineering , John Wiley & Sons, 1994.

Kapur K.C. , Lamberson L. R. Reliability in Engineering Design , John Wiley & Sons, 1977.

Kumamoto H., Henley E.J. Probabilistic Risk Assessment and Management for Engineers , Inst of Electrical Engineers, 1996.

Madsen H.O., Krenk S., Lind N.C.Methods of Structural Safety, Prentice-Hall Inc., 1986.

Olkin I., Gleser L.J., Derman C.Probability Models and Aplications, Macmillan Publishing Co., Inc., 1980.

Tichy M. Applied Methods of Structural Reliability , Kluwer Academic Pub., 1993.

THEMES

Theme 1. Stress Concentration
Theme 2. Fracure Mechanics
Theme 3. Mechanical Properties
Theme 4. Strength of Materials
Theme 5. Theory of Elasticity
Theme 6. Structural Safety
Theme 7. Material Science
Theme 8. Welds
Theme 9.Composite Materials
Theme 10. Finite Element Analysis

MATERIALS SCIENCE

Andrei Burov

CRYSTALLINE SOLIDS

The smallest repeating unit in a crystal is called the unit cell. The geometry and the position of the particles within the unit cell determine the structure of crystalline materials. Three edge lengths (a, b, c) and internal angles (a, b, g) will be used to describe the geometry of a unit cell. There are seven crystal systems and fourteen possible unit cells (Bravais unit cells) depending on the values of a, b, c and a, b, g.

Some of the particles within a unit cell may be shared and therefore do not belong completely to an individual cell. Therefore, in order to calculate number of particles per unit cell we have to consider the following contributions for each particle according to its position:
- atoms centered on the face count 1/2;
- atoms centered on the edge count 1/4;
- atoms centered on the vertex count 1/8
In a simple cubic number of atoms per unit cell = 1; in a body centered cubic - 2; in a face centered cubic - 4.

Atomic packing factor = (Volume of atoms)/(Volume of unit cell). For a simple cubic - atomic packing factor = 0.52; a body centered cubic - 0.68; a face centered cubic - 0.74

To determine a crystallographic direction [uvw] in a unit cell:
1. Find the vector projections on the three axes.
A - 1,0,1; B - 0,1/2,1; C - 0,1,1/2;
D - 1/2,1,0; E - 1,1,0; F - 1,1/2,0.
2. Reduce these coordinates to the 3 smallest integers having the same ratio.
A - [101]; B - [012]; C - [021];
D - [120]; E - [110]; F - [210].

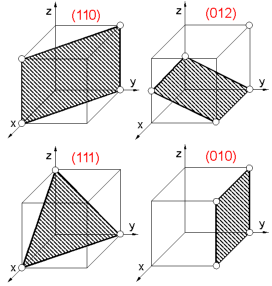A plane within a crystal is defined by the Miller indices. To determine crystallographic (Miller) indices (hkl) of the plane:
1. Find intercepts of a plane on the three axes in terms of the unit cell dimensions.
2. Determine the reciprocals of these numbers.
3. Reduce the reciprocals to the three smallest integers.

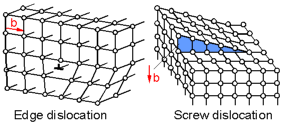There are two main types of planar defects called dislocations - edge dislocation and screw dislocation. A dislocation is a sharp change in the order of atoms along a line. Dislocations move on the slip plane. The magnitude and direction of the slip is defined by the Burger's vector, b. For an edge dislocation the direction of slip is perpendicular to the direction of the dislocation. For a screw dislocation the direction of slip is parallel to the direction of the dislocation.

Slip is known to occur on planes (shown on the picture) in the direction of the maximum density of atoms. This is called a slip system. If there are many slip systems then deformation can occur relatively easily and the metal is considered ductile. BCC crystal structure has up to 48 slip systems. FCC crystal structure has 12 slip systems. HCP crystal structures have only 3 slip systems. Accordingly, most metals with a HCP crystal structure (Mg, Zn, Be) are less ductile than metals with a BCC (W, Fe, K) or FCC (Cu, Al, Ni) structure.

The distance between atoms varies depending on the crystallographic directions. This is the cause of the anisotropy of mechanical and physical properties of a crystal. Therefore, samples cut from a monocrystal in different directions will exhibit a difference in the stiffness. In the FCC and BCC crystals of metals the highest elastic modulus is found in [111] direction, while the lowest is found in the direction of [100]. Real materials consist of many chaotically oriented monocrystals, which results in the isotropy of their properties.

Some materials can exist with different crystal structures. This can be demonstrated by pure iron which has a body centered cubic (BCC) structure at room temperature and a face centered cubic (FCC) structure at 911 _oC. This change is accompanied by shrinkage in volume due to the FCC structure being more closely packed than the BCC structure. The second transformation of crystal structure from FCC to BCC occurs at 1392 _oC.

MECHANICAL PROPERTIES

The mechanical properties of materials are primarily determined subjecting a material sample to a tension test. During a tension test the sample is gradually loaded and the force and corresponding induced elongation are recorded. In order to compare the results obtained with samples of different dimensions the quanitities of stress and strain are utilized.
Stress, s = P/A [N/m=Pa] where P - force applied to the sample; A - cross sectional area of the sample.
Strain, e = Dl/l_o x 100% [%]
where Dl = l - l_o; l - current length; l_o - initial length of the sample;

The basic mechanical properties of a material can be acquired from the stress-strain diargam which results from a tensile test.
To determine the yield stress from a stress-strain curve:
1. Find the point of 0.002 = 0.2% on the strain axis .
2. Draw a line parallel to the elastic region of the curve.
3. The intersection of the line and stress-strain curve corresponds to the yield stress of the material.

The ultimate tensile strength is defined as the maximum value of stress reached in tensile test before fracture of the sample.
Ductility can be determined in a material with the use of the following:
Elongation = (l_f - l_o)/l_o x 100%
Reduction in area = (A_f - A_o)/A_o x 100%
where indexes o and f correspond to initial and final values at fracture respectivily.

The measure of material stiffness is defined as the elastic modulus. This quantity is determined from the initial range of the stress-strain diagram during which the material exhibits linear elastic behavior. In this region the sample will return to its original shape and dimensions upon unloading.
Elastic modulus, E = s/e [Pa]
The resistance to deformation in a material increases as the magnitude of the elastic modulus becomes greater.

Consider a test when a material is loaded beyond its yield stress. Upon unloading the stress follows a line parallel to the elastic range of the stress-strain curve. Futhermore, only the elastic deformation is recovered. The yield stress of a plastically deformed material is higher than its initial value. Upon reapplying the load the material deforms elastically until the new yield stress is reached. It should be noted that the elastic modulus of the material remains constant.

Hardness is the ability of a material to resist the indentation of a harder solid. The most common hardness tests are accomplished by forcing a small indenter into the surface of the sample material.
The picture shows the setup of the Brinell's hardness test. In general, hardness is proportional to the tensile strength of the material as both characteristics show a resistance of the material to plastic deformation.

FAILURE

The Fatigue curve or S-N curve is a plot of the number of cycles that a specimen will sustain at various levels of alternating stress or strain before failure. The maximum stress, minimum stress or stress amplitude can be utilized in the plot. A log scale is often used for the N axis.
The S-N curves of materials such as high strength steels, aluminum alloys or materials in an aggressive environment do not have the horizontal segment.
Fatigue Strength is the maximum stress that can be applied repeatedly for a specific number of cycles without leading to fracture. This quantity is usually determined directly from the S-N diagram.

Specimen loading (tension, bending or torsion) and a level of applied nominal stress can be indentified by examining the fracture surfaces. The fatique area has a fine structure outline and occupies nearly the whole section of a specimen if the applied stress is low. Similarly, a specimen which has endured a higher stress displays a smaller fatigue zone and a larger rupture zone.

Площадь под кривая напряжение деформация представляет работу, необходимую для разрушения материала. Соответственно, чем больше площадь, тем больше работы необходимые для отказа фирмы. Пластичные материалы имеют обширные пластической деформации и высокое поглощение энергии до разрушения. Пластической деформации и поглощение энергии хрупких материалов являются относительно низкими.

Низкая температура уменьшается способность материала к пластической деформации. Материалы, которые пластичного при комнатной температуре показывают хрупкому разрушению при низких температурах. Исключение, такое поведение является большинство of materials with an FCC structure, which remain ductile at very low temperatures. At a narrow temperature range the crack resistance falls drastically. This is known as the ductile-to-brittle transition.

Creep is the gradual increase of plastic deformation of a material under a constant stress, which is less than the yield stress. Creep is pronounced at temperatures above 0.4 of the melting point (taken in oK). The greater the service temperature or applied stress, the less time the material takes to fracture due to creep.

The maximum stress, near the tip of an elliptical opening, perpendicular to the applied stress in a plane is determined from the following:
smax = s x [1 + 2 x (a/r)^1/2]
where s is the applied stress; r is the radius of curvature at the tip; a is the half length for an internal opening and the full length for a surface opening.

Critical stress intensity factor K_IC or fracture toughness demonstrates the resistance of a material to the crack propagation. Damaged materials with higher fracture toughness can sustain a higher stress.
The maximum nominal stress that a structural element with a crack can sustain, is determined as:
s = K_IC / [Y (p x a)^1/2]
where a is the half of the crack length; Y is a dimensionless factor depending on geometry. For a through internal crack that is much smaller than the dimensions of the element Y=1, for a surface crack Y=1.12.

PHASE DIAGRAMS

A binary phase diagram is composed from the cooling curves of alloys with various compositions. For an alloy with a particular composition there are two points on the curve where a cooling rate is affected. The first point corresponds to the temperature at which the alloy begins to solidify. On the phase diagram this point belongs to the Liquidus line. The second point corresponds to the temperature at which the entire liquid has solidified. On the phase diagram this point belongs to the Solidus line.

This diagram dispays the complete liquid and solid solubility of two component otherwise known as a binary isomorphous system. This occurs when the components have the same crystal structure and approximately the same radii, electro negativity and valence. For instance, systems of Ni-Cu and Ag-Au exhibit this type of diagram.
At the temperature T₁ for an alloy of 50%M + 50%N:
Composition of solid solution a is determined at point c - 30%M +70%N.
Composition of Liquid is determined at point a - 80%M +20%N.
% Liquid = bc/ac • 100% = (70-50)/(70-20) · 100 % = 40%
% a = ab/ac • 100% = (50-20)/(70-20) · 100 % = 60%

The following diagram displays the complete liquid and limited solid solubility of two components otherwise known as the binary eutectic system. There are two solid phases (solid solutions): a - rich in the component M and b - rich in the component N.
At point O (Eutectic point) three phases (one liquid and two solid phases) coexist simultaneously at the eutectic composition and temperature.

Line bd or the Solvus line protrays the change of the maximum concentration of component M in component N. At the temperature T₁ the maximum concentration M in N is 10%. The highest possible solubility of the component M in component N (and vise verse) is found at the eutectic temperature. On the diagram this constant temperature line goes through the eutectic point O.

All alloys with composition along line ab comprise the eutectic structure which alternates layers of a and b phases. The closer the alloy to the eutectic composition, the higher amount of the eutectic it contains. The solidified alloys within line ab is a mixture of a grains precipitated prior to the eutectic reaction and grains of the eutectic. While the alloys on the right from point O - mixture of b and the eutectic grains.