 |
Главная |
ТЕМА 2.3 Стандартизация моделирования функциональных структур объектов машиностроения
|
из
5.00
|
Студент должен иметь представление:
– о функциональных структурах стандартной промышленной продукции, классифицированной по физическим процессам, с выделением функциональных свойств (метрические, механические, кинематические, динамические, энергетические) для материальных и информационных (абстрактных) комплексов;
Студент должен уметь:
– рассчитывать размерные цепи методом полной взаимозаменяемости (максимум-минимум)
Научно-методический подход стандартизации в моделировании функциональных структур. Моделирование размерных цепей. Моделирование точности размерных цепей фланцевых соединений. Моделирование электронных цепей.
Литература: [2], с.278-284; [6], с.133-144; [7], с.485-508; [8], с.68-85; [36].
Вопросы для самоконтроля:
1. Что называется размерной цепью?
2. Какие звенья цепи называются увеличивающимися, какие уменьшающими?
3. Охарактеризуйте принцип расчета обратной задачи.
Методические указания
В изделии, изготовленном на предприятии, детали занимают одна относительно другой определенное положение в соответствии с их функциональным назначением. Поэтому размеры деталей в изделии находятся во взаимосвязи. Размерные связи детали или изделия анализируются с помощью теории размерных цепей.
Размерная цепь – совокупность размеров, образующих замкнутый контур. С помощью размерных цепей определяют операционные допуски, пересчитывают конструкторскую базу на технологическую, выбирают измерительную базу.
Размеры, входящие в размерную цепь, называются звеньями (замыкающие, составляющие).
Замыкающее звено (АО) – размер не обрабатываемый, получающийся в порядке выполнения технологических операций изготовления или сборке узла, на чертеже обозначается без допуска, в сборочных цепях определяет размер зазора, натяга или расстояния до какой-либо поверхности от базы в сборочной цепи.
Составляющие звенья по отношению к замыкающему звену делятся на увеличивающие (А) (при увеличении которых замыкающий размер увеличивается) и уменьшающие (А¯) (при увеличении которых замыкающий размер уменьшается).
В теории размерных цепей решаются два типа задач:
Первая задача (обратная). Определение предельных размеров (отклонений) замыкающего размера по заданным предельным размерам (отклонениям) составляющих размеров. Это в основном проверочный расчет методом максимум-минимум.
Вторая задача (прямая). Определение предельных размеров (отклонений) всех составляющих размеров размерной цепи по заданным предельным размерам (отклонениям) замыкающего размера. Эта задача относится к проектному расчету размерной цепи.
Пример. По заданным размерам и полям допусков составляющих звеньев детали (рисунок 2.3.1) рассчитать замыкающее звено.

Рисунок 2.3.1
Решение. Составляем схему размерной цепи (рисунок 2.3.2) из нее устанавливаем, что звенья А2 и А3 являются уменьшающими, а звено А1 – увеличивающее.




Рисунок 2.3.2 – Схема размерной цепи
Расчет производим методом максимум-минимум.
Допуски звеньев выписываем из таблицы предельных отклонений полей допусков гладких соединений.
ТА1=74мкм; ТА2=30мкм; ТА3=36мкм
Предельные отклонения звеньев, мкм:
ES(A1) = 0; EI(A1) = -74;
ES(A2) = 30; EI(A2) = 0;
ES(A3) = 36; EI(A3) = 0;
Вычисляем по формуле номинальное значение замыкающего звена.
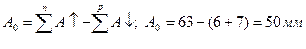 ,
,
где n – число увеличивающих звеньев
р – число уменьшающих звеньев
Выписываем предельные размеры замыкающего звена по формулам:


Вычисляем отклонения замыкающего звена по формулам:


Допуск замыкающего звена определяем по формуле:
ТА0=ES(А0)-EI(А0); ТА0=0-(-140)=140мкм
Ответ: А0=50-0,140
Практическое занятие.
|
из
5.00
|
Обсуждение в статье: ТЕМА 2.3 Стандартизация моделирования функциональных структур объектов машиностроения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

