 |
Главная |
Аналитические свойства оператора прямой задачи гравиметрии для распределения плотности
|
из
5.00
|
Будем рассматривать в качестве модели среды – введенную в 2.1.1 модель распределения плотности в заданной области 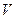 нижнего полупространства. В соответствии с (2.2) запишем связь между распределением плотности
нижнего полупространства. В соответствии с (2.2) запишем связь между распределением плотности  в области
в области 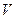 , целиком лежащей в нижнем полупространстве
, целиком лежащей в нижнем полупространстве  , и вертикальной производной гравитационного потенциала в виде:
, и вертикальной производной гравитационного потенциала в виде:
 (7.1)
(7.1)
Напомним, что координатные оси  и
и  совмещены, а ось
совмещены, а ось  направлена верх – противоположно оси
направлена верх – противоположно оси  . На первом этапе считаем, что вертикальная производная гравитационного потенциала задана на всей плоскости
. На первом этапе считаем, что вертикальная производная гравитационного потенциала задана на всей плоскости  :
:  . Тем самым, как хорошо известно, определены значения
. Тем самым, как хорошо известно, определены значения  в любой точке области
в любой точке области  - верхнего полупространства. В том числе и на поверхности произвольного рельефа, заданного функцией
- верхнего полупространства. В том числе и на поверхности произвольного рельефа, заданного функцией  . Значение это находится с помощью известного интеграла Пуассона (см. 2.1.4, формула (2.6)), дающего решение задачи Дирихле для полупространства:
. Значение это находится с помощью известного интеграла Пуассона (см. 2.1.4, формула (2.6)), дающего решение задачи Дирихле для полупространства:
 . (7.2)
. (7.2)
Обозначим, кроме того  – горизонтальную полосу в нижнем полупространстве (Е_), ограниченную по вертикали координатами
– горизонтальную полосу в нижнем полупространстве (Е_), ограниченную по вертикали координатами  В частности, область
В частности, область 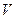 может совпадать с
может совпадать с  , либо быть ее собственным подмножеством. Соотношение (1), в соответствие с введенными ранее соглашениями об обозначениях операторов для прямой задачи, будем записывать в форме:
, либо быть ее собственным подмножеством. Соотношение (1), в соответствие с введенными ранее соглашениями об обозначениях операторов для прямой задачи, будем записывать в форме:
 ,
,
где 
Следующий результат характеризует свойства непрерывности оператора 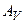 .
.
Теорема 1. Пусть V – ограниченная область, целиком лежащая в  . Тогда
. Тогда 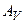 – линеен и ограничен из
– линеен и ограничен из  в
в  для всех
для всех  . Для случая
. Для случая  оператор
оператор  – линеен и ограничен из
– линеен и ограничен из  в
в  при
при 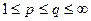 .
.
Обозначим  - норму оператору
- норму оператору 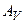 , действующего из
, действующего из  в
в  . Тогда при ограниченной области
. Тогда при ограниченной области 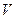 :
:
 ,
,
где введены обозначения  .
.
Для случая  и
и 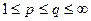 величина
величина  ограничена и при
ограничена и при  :
:
 .
.
В случае, когда q, либо одновременно q и p равны бесконечности:
 ,
, 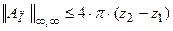 .
.
Доказательство. Линейность – очевидное свойство введенного оператора. Доказать следует лишь его непрерывность в тех, либо иных, функциональных пространствах. Для краткости вместо:

будем писать
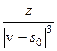 , имея в виду, что
, имея в виду, что  пространственная координата точки в области
пространственная координата точки в области  .
.
Из (1) имеем:

Далее:


Следовательно:

В силу теоремы Риса о выпуклости (прил.2), для  имеем:
имеем:

Следовательно:

Тогда для  легко получаем:
легко получаем:
 .
.
Приведенная оценка является грубой. Она может быть улучшена для случая  . Заметим при этом, что если
. Заметим при этом, что если 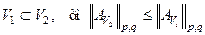 . Таким образом,
. Таким образом,  .
.
Применим к соотношению (1) неравенство Юнга, рассматривая в качестве области V полосу П:
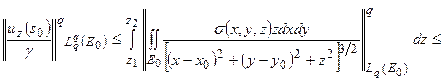
 .
.
Здесь  связаны условием:
связаны условием:
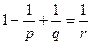 .
.
Заметим, что, если 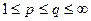 , то это условие может быть выполнено при
, то это условие может быть выполнено при  .
.
Оценим величину:
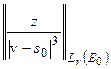 .
.
Для этой цели вновь применим теорему Риса о выпуклости  :
:
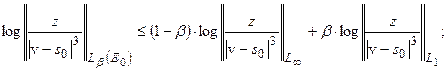
 .
.
Но:
 .
.
Следовательно:

Тогда:
 . .
| (7.3) |
Из (3) следует, что при 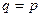 и следующем отсюда
и следующем отсюда  :
:
 . (7.4)
. (7.4)
Теперь имеем следующую цепочку оценок:
 ; (7.5)
; (7.5)
 ; (7.6)
; (7.6)
 . (7.7)
. (7.7)
Из приведенных соотношений и неравенств Риса о выпуклости сразу следует вывод об ограниченности  для
для  . Рассмотрим теперь случай
. Рассмотрим теперь случай 
Обозначим  . Понятно, что:
. Понятно, что:


 .
.
Одно из утверждений теоремы доказано.
Оценим далее  , пользуясь для этого (4-7) и неравенством выпуклости:
, пользуясь для этого (4-7) и неравенством выпуклости:

Полагая  , получим:
, получим:
 . (7.8)
. (7.8)
Теперь, используя (7) и неравенство выпуклости, найдем оценку для  , где
, где  :
:
 .
.

Примем  , а β выберем так, чтобы
, а β выберем так, чтобы  .
.
Тогда  , при этом
, при этом  . Тогда:
. Тогда:
 .
.
Пользуясь обозначением  , где p≤q , получим:
, где p≤q , получим:
 ,
,
или после упрощения:
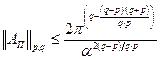 ,
,
что и требовалось доказать.
Итак, мы выяснили, что оператор 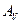 является “хорошим” для решения прямых задач, поскольку линеен и ограничен во всех обозримых для приложения пространствах. Дифференцируя уравнение (1) по переменным
является “хорошим” для решения прямых задач, поскольку линеен и ограничен во всех обозримых для приложения пространствах. Дифференцируя уравнение (1) по переменным  , как по параметрам и, полагая z0 = 0, получим новые операторы, соответствующие расчету высших производных гравитационного потенциала. Повторяя приведенные рассуждения, легко доказать, что вновь полученные операторы обладают теми же свойствами, что сформулированы в теореме 1. По тем же причинам непрерывен оператор
, как по параметрам и, полагая z0 = 0, получим новые операторы, соответствующие расчету высших производных гравитационного потенциала. Повторяя приведенные рассуждения, легко доказать, что вновь полученные операторы обладают теми же свойствами, что сформулированы в теореме 1. По тем же причинам непрерывен оператор 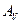 из
из  в
в  и т.д. Однако нас, в большей мере, интересует обратная задача, и главным свойством является ее разрешимость. Следует выявить, при каких правых частях уравнение (1) разрешимо, является ли решение единственным и будит ли оно устойчивым. Для простоты дальнейших рассмотрений ограничимся случаем, когда
и т.д. Однако нас, в большей мере, интересует обратная задача, и главным свойством является ее разрешимость. Следует выявить, при каких правых частях уравнение (1) разрешимо, является ли решение единственным и будит ли оно устойчивым. Для простоты дальнейших рассмотрений ограничимся случаем, когда 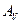 действует из
действует из 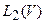 в
в  .
.
Теорема 2. Пусть 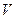 – область в
– область в  , целиком лежащая в П и содержащая некоторый шар в
, целиком лежащая в П и содержащая некоторый шар в  . Тогда
. Тогда  образует в
образует в  плотное множество[29].
плотное множество[29].
Доказательство. Воспользуемся тем фактом, что плотность  в
в  эквивалентна однозначной разрешимости сопряженного уравнения. Действительно, поскольку
эквивалентна однозначной разрешимости сопряженного уравнения. Действительно, поскольку 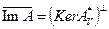 , то из условия
, то из условия  следует
следует  и
и  . Вид сопряженного к
. Вид сопряженного к 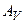 оператора
оператора  , отображающего пространство
, отображающего пространство  в подпространство в
в подпространство в 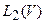 , определен соотношением:
, определен соотношением:

| (7.9) |
Где  – проектор из
– проектор из  на
на 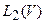 . Это следует из следующей цепочки равенств:
. Это следует из следующей цепочки равенств:

| (7.10) |
Легко заметить, что  - множество гармонических в V и непрерывных на границе V функций, имеющих единственное аналитическое продолжение на все E_ (так как V содержит некоторый шар). Но равенство нулю гармонической функции внутри некоторого шара влечет ее равенство нулю всюду в области гармоничности. В частности, из:
- множество гармонических в V и непрерывных на границе V функций, имеющих единственное аналитическое продолжение на все E_ (так как V содержит некоторый шар). Но равенство нулю гармонической функции внутри некоторого шара влечет ее равенство нулю всюду в области гармоничности. В частности, из:
 ,
,
следует, что уравнение  имеет единственное решение
имеет единственное решение  . Таким образом,
. Таким образом,  , теорема доказана.
, теорема доказана.
Из приведенного результата следует вывод о том, что уравнение (1) может быть решено как угодно точно для любой правой части из  . Но разрешимость с любой наперед заданной точностью не означает строгой разрешимости. В каком-то смысле, элементов из
. Но разрешимость с любой наперед заданной точностью не означает строгой разрешимости. В каком-то смысле, элементов из  , для которых уравнение (1) не имеет строгого решения, даже больше, чем тех, для которых имеет, т.е. чем
, для которых уравнение (1) не имеет строгого решения, даже больше, чем тех, для которых имеет, т.е. чем  . Более строгий смысл придает сказанному .
. Более строгий смысл придает сказанному .
Теорема 3. Пусть  , тогда
, тогда  образует
образует  множество первой категории.
множество первой категории.
Доказательство. Напомним, что М есть множество первой категории, если оно представимо, как не более, чем счетное объединение нигде не плотных множеств. Множество называется нигде не плотным, если его замыкание не содержит внутренних точек.
Выберем плоскость  , определенную значением вертикальной координаты
, определенную значением вертикальной координаты  , что возможно в силу определения П. (см. рис. 1).
, что возможно в силу определения П. (см. рис. 1).
Значение поля  на
на  от распределения масс в V равно:
от распределения масс в V равно:
 .
.
 В силу доказанной выше теоремы 1 о непрерывности оператора (1)
В силу доказанной выше теоремы 1 о непрерывности оператора (1)  и, следовательно,
и, следовательно,  , где
, где 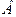 оператор, определенный как интеграл Пуассона:
оператор, определенный как интеграл Пуассона:
 .
.
Следовательно,  . Осталось показать, что
. Осталось показать, что  множество первой категории.
множество первой категории.
Пусть S – замкнутый единичный шар в  . Поскольку для любого
. Поскольку для любого 
 ,
,
то 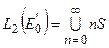 . Тогда
. Тогда  , где
, где  – образ
– образ  при отображении
при отображении 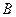 . В силу ограниченности
. В силу ограниченности 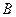 и рефлексивности
и рефлексивности  , каждое из
, каждое из  замкнуто как образ замкнутого выпуклого множества. Если
замкнуто как образ замкнутого выпуклого множества. Если  – множество второй категории, то хотя бы для одного n Ωn, в силу замкнутости, имеет внутреннюю точку. Но если оператор (линейный и ограниченный) отображает замкнутый шар во множество, имеющее внутреннюю точку, то обратный к этому оператору ограничен. Покажем теперь, что оператор
– множество второй категории, то хотя бы для одного n Ωn, в силу замкнутости, имеет внутреннюю точку. Но если оператор (линейный и ограниченный) отображает замкнутый шар во множество, имеющее внутреннюю точку, то обратный к этому оператору ограничен. Покажем теперь, что оператор 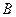 не имеет ограниченного обратного, как оператор из
не имеет ограниченного обратного, как оператор из  в себя (в
в себя (в  ).
).
Рассмотрим уравнение  :
:
 (7.11)
(7.11)
Выберем последовательность монотонно убывающих чисел  , предел которых равен
, предел которых равен  , и соответствующую им, параметризированных числами
, и соответствующую им, параметризированных числами  последовательность функций:
последовательность функций:
 .
.
Ясно, что 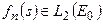 , так как
, так как  и по теореме Рисса о выпуклости:
и по теореме Рисса о выпуклости:

Последовательности  соответствует последовательности
соответствует последовательности
 ,
,
Поскольку, как это следует из (11):
 .
.
Однако последовательность  не имеет предела в
не имеет предела в  , в то время как последовательность
, в то время как последовательность  такой предел имеет:
такой предел имеет:
 .
.
Итак, имеем:  , однако
, однако  не существует в
не существует в  . Но это не совместимо с предположением ограниченности оператора
. Но это не совместимо с предположением ограниченности оператора 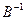 как действующего из
как действующего из  в
в  . Таким образом, приходим к выводу, что
. Таким образом, приходим к выводу, что 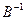 не ограничен и, следовательно,
не ограничен и, следовательно,  не имеет внутренней точки. Тогда
не имеет внутренней точки. Тогда  есть множество первой категории, что и требовалось доказать.
есть множество первой категории, что и требовалось доказать.
Замечание: Все рассмотренные последовательности принадлежат и  . Следовательно, приведенный пример “работает” во всех этих пространствах. Более того, основным моментом в доказательстве теоремы является вывод о замкнутости образа S при отображении В. Это имеет место для всех рефлексивных пространств, и теорема 3 верна для всех
. Следовательно, приведенный пример “работает” во всех этих пространствах. Более того, основным моментом в доказательстве теоремы является вывод о замкнутости образа S при отображении В. Это имеет место для всех рефлексивных пространств, и теорема 3 верна для всех  .
.
Рассмотрим теперь вопрос о единственности решения уравнения (1), предполагая, что хотя бы одно решение существует. В силу линейности оператора 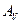 , утверждению о существовании более чем одного решения уравнения (1) эквивалентно утверждение о существовании ненулевых решений уравнения
, утверждению о существовании более чем одного решения уравнения (1) эквивалентно утверждение о существовании ненулевых решений уравнения  . Последнее означает, что ядро
. Последнее означает, что ядро  оператора
оператора 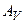 содержит и ненулевые элементы. Действительно, если два распределения плотности
содержит и ненулевые элементы. Действительно, если два распределения плотности 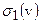 и
и  удовлетворяют одному и тому же уравнению
удовлетворяют одному и тому же уравнению  , то
, то  удовлетворяет уравнению
удовлетворяет уравнению  .
.
Простейший и известный еще Ньютону пример гравитационной эквивалентности двух различных тел – это совпадение внешних гравитационных полей от двух однородных по плотности шаров с общим центром и массой, но различной плотности и, как следствие, различного радиуса. Уже из этого примера можно заключить, что ядро оператора 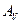 содержит более одного элемента.
содержит более одного элемента.
Полное описание ядра оператора 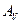 дает следующая теорема.
дает следующая теорема.
Теорема 4 (П.С.Новиков). Пусть V – замкнутая регулярная область. Для того, чтобы распределение плотности  создало нулевой внешний потенциал, необходимо и достаточно, чтобы для любой гармонической в V и непрерывной на границе
создало нулевой внешний потенциал, необходимо и достаточно, чтобы для любой гармонической в V и непрерывной на границе 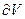 области V функции
области V функции  выполнялось равенство
выполнялось равенство
 . (7.12.)
. (7.12.)
По сути это означает, что ядро  оператора
оператора 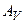 ортогонально множеству гармонических в V и непрерывных на
ортогонально множеству гармонических в V и непрерывных на 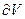 функций.
функций.
Замечание 1. Теорема не распространяется на случай, когда в качестве области 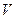 выступает полоса
выступает полоса  , поскольку последняя не замкнута. Более того, далее будет показано, что для случая
, поскольку последняя не замкнута. Более того, далее будет показано, что для случая  существуют гармонические в
существуют гармонические в  функции, с нулевой правой частью для (1).
функции, с нулевой правой частью для (1).
Замечание 2. Существенным является и требование, чтобы нулю равнялась правая часть в (1) только всюду на 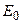 . Далее будет показано, что для любого конечного множества точек
. Далее будет показано, что для любого конечного множества точек 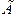 из
из 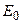 , или более обще
, или более обще  , существует гармоническая в V функция, для которой правая часть в (1) отображается в ноль во всех точках
, существует гармоническая в V функция, для которой правая часть в (1) отображается в ноль во всех точках  .
.
Теорему 3 можно легко вывести из теоремы о ядре (см. приложение 2.4). Действительно, согласно теореме о ядре 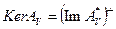 . Поскольку
. Поскольку  - множество гармонических в V функций, представимых в виде интеграла Пуассона, замыкание которых для регулярной области V есть также гармонические в V функции, непрерывные на границе
- множество гармонических в V функций, представимых в виде интеграла Пуассона, замыкание которых для регулярной области V есть также гармонические в V функции, непрерывные на границе 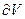 , то и получаем требуемый результат.
, то и получаем требуемый результат.
Теорема о ядре позволяет сформулировать результат о единственности решения уравнения (1) и для поточечно заданного поля.
Теорема 5. Пусть область V ограничена и замкнута. Для того чтобы распределение плотности создавало нулевую вертикальную производную гравитационного потенциала в N точках  , необходимо и достаточно, чтобы для любой из N функций
, необходимо и достаточно, чтобы для любой из N функций
 ,
,
выполнялось условие:
 .
.
Для доказательства достаточно применить теорему о ядре, в соответствии с которой  к оператору:
к оператору:
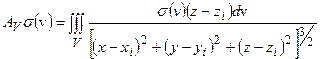 , отображающему
, отображающему 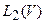 в систему из
в систему из  значений поля
значений поля  , образующих конечномерное пространство
, образующих конечномерное пространство  с Евклидовой нормой.
с Евклидовой нормой.
Для того чтобы найти сопряженный этому оператору, выберем произвольный вектор 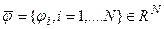 из сопряженного к
из сопряженного к  пространства, совпадающего с самим
пространства, совпадающего с самим  , и запишем цепочку равенств:
, и запишем цепочку равенств:

Следовательно, искомый сопряженныйимеет вид:

Ясно, что из условия  следует, что для любого элемента
следует, что для любого элемента  и
и  выполнено
выполнено  . Но тогда выполнено и (12) .
. Но тогда выполнено и (12) .
Из теоремы П.С.Новикова следует, что множество гармонических и непрерывных на границе ограниченной, регулярной, замкнутой области V есть класс единственности. Условие ограниченности области, как это было отмечено в замечании 1 весьма существенно. Без этого условия теорема не работает.
Покажем, что если область V не ограничена, то существует гармонические распределения плотности в V с нулевым значением вертикальной производной гравитационного потенциала на  .
.
К уравнению  применим преобразование Фурье (по
применим преобразование Фурье (по  ). Получим:
). Получим:
 (7.13)
(7.13)
Где  - есть преобразование Фурье функций
- есть преобразование Фурье функций  и
и  по переменным
по переменным  соответственно (напомним, что оси
соответственно (напомним, что оси  и
и  совмещены), а
совмещены), а  .
.
Будем искать теперь решение уравнения (13) в виде
 и
и  соответственно. Здесь:
соответственно. Здесь:  - искомые функции. После тривиальныхподстановок выражений для
- искомые функции. После тривиальныхподстановок выражений для  и
и 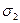 в (13) получаем:
в (13) получаем:
 (7.14)
(7.14)
 . (7.15)
. (7.15)
Если функцию  выбрать так, чтобы функция
выбрать так, чтобы функция  была квадратично интегрируемой при
была квадратично интегрируемой при  и, следовательно, квадратично интегрируемо и ее обратное преобразование Фурье для этих значений
и, следовательно, квадратично интегрируемо и ее обратное преобразование Фурье для этих значений 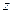 , то, в силу неравенств
, то, в силу неравенств  и
и
 ,
,
формулой (14) определен некоторый элемент из  , преобразование Фурье (обратное) которого есть гармоническая функция. Точно также обратное преобразование Фурье функции (15) по переменным
, преобразование Фурье (обратное) которого есть гармоническая функция. Точно также обратное преобразование Фурье функции (15) по переменным  есть гармоническая функция, и наложенных ранее условий на
есть гармоническая функция, и наложенных ранее условий на  достаточно, чтобы соотношением (15) была определена функция из
достаточно, чтобы соотношением (15) была определена функция из 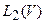 . Каждая из них соответствует одному и тому же полю, спектр которого есть
. Каждая из них соответствует одному и тому же полю, спектр которого есть  . Беря их разность, получаем, что соотношением
. Беря их разность, получаем, что соотношением
 (7.16)
(7.16)
определена функция, обратное преобразование Фурье которой по переменным  есть гармоническая функция (в силу гармоничности
есть гармоническая функция (в силу гармоничности 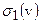 и
и  ), и этой функции соответствует нулевое значение вертикальной производной гравитационного потенциала на
), и этой функции соответствует нулевое значение вертикальной производной гравитационного потенциала на  . Таким образом, для неограниченной области существуют гармонические функции, принадлежащие ядру оператора прямой задачи с полем на
. Таким образом, для неограниченной области существуют гармонические функции, принадлежащие ядру оператора прямой задачи с полем на  .
.
Поскольку 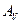 - линейный ограниченный оператор из
- линейный ограниченный оператор из  в
в  , то
, то 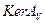 - замкнутое пространство в
- замкнутое пространство в  . Следовательно, можно определить фактор-пространство
. Следовательно, можно определить фактор-пространство  пространства
пространства  по ядру оператора
по ядру оператора 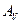 . Это пространство состоит из классов смежности, вместе с заданным элементом, содержащим и все элементы, эквивалентные ему по гравитационному полю. Иными словами, классами смежности являются всевозможные элементы вида
. Это пространство состоит из классов смежности, вместе с заданным элементом, содержащим и все элементы, эквивалентные ему по гравитационному полю. Иными словами, классами смежности являются всевозможные элементы вида  . Легко проверить, что два класса смежности либо совпадают, либо не пересекаются. Оператор
. Легко проверить, что два класса смежности либо совпадают, либо не пересекаются. Оператор 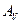 , рассматриваемый на фактор - пространстве
, рассматриваемый на фактор - пространстве  , уже является взаимнооднозначным и непрерывным, если норму
, уже является взаимнооднозначным и непрерывным, если норму  в
в  определить условием:
определить условием:
 . (7.17)
. (7.17)
Область значений этого оператора совпадает с областью значений оператора 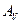 , а область определения есть банахово пространство, состоящее из описанных классов смежности. Тогда, в силу доказанной теоремы 3,
, а область определения есть банахово пространство, состоящее из описанных классов смежности. Тогда, в силу доказанной теоремы 3, 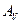 не может иметь ограниченного обратного. Эквивалентное этому утверждению – сужение
не может иметь ограниченного обратного. Эквивалентное этому утверждению – сужение 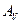 на
на  не имеет ограниченного обратного.
не имеет ограниченного обратного.
Проведенный анализприводит к следующим выводам:
1. Обратная задача в классе распределений плотности может быть решена для любой правой части из  с любой наперед заданной точностью.
с любой наперед заданной точностью.
2. Решение неединственное и определено с точностью до произвольного элемента из 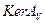 , являющегося замкнутым подпространством в
, являющегося замкнутым подпространством в  .
.
3. Оператор 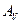 , определенный на подпространстве в
, определенный на подпространстве в  , состоящем из распределений, принадлежащих
, состоящем из распределений, принадлежащих  , не имеет ограниченного обратного. Иными словами, сужение
, не имеет ограниченного обратного. Иными словами, сужение 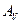 с
с  на
на  не имеет ограниченного обратного.
не имеет ограниченного обратного.
Таким образом, обратная задача гравиметрии является некорректной. Для нее не выполнено ни одного из условий корректности по Адамару.
В процессе доказательства того, что множество значений оператора (1) есть множество первой категории в  при 1<p<∞, было показано, что таковой является и область значений оператора (11), доставляющего решение задачи Дирихле для полупространства. Это означает, что обратная задача для (11) является неустойчивой из
при 1<p<∞, было показано, что таковой является и область значений оператора (11), доставляющего решение задачи Дирихле для полупространства. Это означает, что обратная задача для (11) является неустойчивой из  в
в  и, кроме того, не для всех
и, кроме того, не для всех 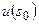 из
из  она разрешима. Итак, для задачи аналитического продолжения потенциального поля в нижнее полупространство (обратная задача к аналитическому продолжению поля в верхнее полупространство, доставляемому интегралом Пуассона): решение не всегда существует, решение не устойчиво из
она разрешима. Итак, для задачи аналитического продолжения потенциального поля в нижнее полупространство (обратная задача к аналитическому продолжению поля в верхнее полупространство, доставляемому интегралом Пуассона): решение не всегда существует, решение не устойчиво из  в
в  .
.
Нетрудно доказать и то, что оператор В имеет в качестве области значений множество первой категории и в пространстве непрерывных на  функций
функций  . Для этого следует продемонстрировать неограниченность обратного оператора на пространстве функций
. Для этого следует продемонстрировать неограниченность обратного оператора на пространстве функций  . Рассмотрим множество из
. Рассмотрим множество из  функций, производная которых в направлении оси 0Y равна нулю (выполнены условия двухмерности). Тогда аналог соотношение (11) запишется так:
функций, производная которых в направлении оси 0Y равна нулю (выполнены условия двухмерности). Тогда аналог соотношение (11) запишется так:
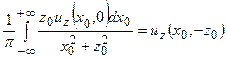 ,
,
где  и
и  - след на оси
- след на оси  функций
функций  и
и  , соответственно. Выберем в качестве
, соответственно. Выберем в качестве  . Тогда под интегралом, для того чтобы он превратился в тождество, необходимо поставить вместо
. Тогда под интегралом, для того чтобы он превратился в тождество, необходимо поставить вместо  функцию
функцию  . При
. При  последовательность
последовательность  слабо сходится к нулю, в тоже время
слабо сходится к нулю, в тоже время  , при
, при  не является слабо сходящей последовательностью. Это противоречит требованию непрерывности. Таким образом, оператор, обратный к В, не является слабо непрерывным, тем более он не является и сильно непрерывным.
не является слабо сходящей последовательностью. Это противоречит требованию непрерывности. Таким образом, оператор, обратный к В, не является слабо непрерывным, тем более он не является и сильно непрерывным.
|
из
5.00
|
Обсуждение в статье: Аналитические свойства оператора прямой задачи гравиметрии для распределения плотности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

