 |
Главная |
Уравнивание нивелирной сети способом красных чисел ( Попова В.В.)
|
из
5.00
|
Схема для уравнивания нивелирных полигонов по способу профессора Попова В.В.
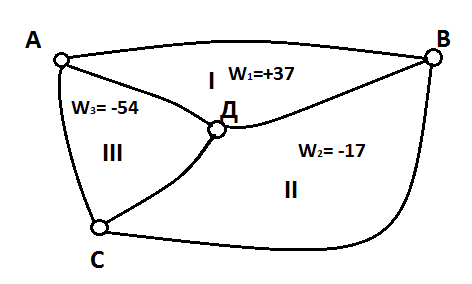
Исходные данные:
| № варианта | Длины ходов в км | Невязки полигонов, мм | |||||||
| АВ | ВС | СА | АД | ДВ | ДС | W1 | W2 | W3 | |
| 21,2 | 18,6 | 9,6 | 9,2 | 6,6 | 21,1 | +37 | -17 | -54 |
На схеме уравнивания нивелирной сети в центре каждого полигона строим рамки, внутри которых записывают невязки(  ,
,  ,
,  ) Вне полигона у каждого его звена строим рамки для записи поправок( (I),(II),(III)); у внешних будет по одной рамке, а у внутренних – по две.
) Вне полигона у каждого его звена строим рамки для записи поправок( (I),(II),(III)); у внешних будет по одной рамке, а у внутренних – по две.
Вычисляем красные числа для всех звеньев полигонов
Р1 = АВ + ДВ+ АД = 37
Р2 = ДВ + ВС + ДС = 46,3
Р3 = ДС + СА + АД = 39,9
Красное число хода равно длине хода, деленное на периметр полигона.
Так для первого полигона
Кр.АВ1 = 21,2/37 = 0,57
Кр.АД1,3 = 9,2/37 = 0,25
Кр.ВД1,2 = 6,6/37 = 0,18
Для второго полигона
Кр.ВС2 = 18,6/46,3 = 0,40
Кр.ВД2,1 = 6,6/46,3 = 0,14
Кр.СД2,3 = 21,1/46,3 = 0,46
Для третьего полигона
Кр.АС3 = 9,6/39,9 = 0,24
Кр.СД3,2 = 21,1/39,9 = 0,53
Кр.АД3,1 = 9,2/39,9 = 0,23
Красные числа обозначаем красным цветом над соответствующими рамками, расположенными вне полигона около его звеньев.
Контроль. Для каждого полигона сумма красных чисел должна быть равна единице.
0,57 + 0,25 + 0,18 = 1; 0,40 + 0,14 + 0,46 = 1; 0,24 + 0,53 + 0,23 = 1
Распределение невязок в полигонах производят пропорционально красным числам звеньев, начиная с полигона с наибольшей по абсолютному значению невязкой. ( полигон III, т.к. WIII = -54)
Поправка, приходящая на звено, определяется как произведение невязки полигона на красное число звена:
VIII = WIII* Кр.АС3 = -54*0,24 = -13
VIII,I = WIII* Кр.АД3,1 = -54*0,23 = -12
VIII,II = WIII* Кр.СД3,2 = -54*0,53 = -29
Контроль: сумма поправок равна невязке полигона:
-13+(-12)+(-29) = -54
Полученные поправки по звеньям записываем в соответствующие рамки.
В следующем полигоне  значение исходной невязки +37мм. изменится на величину поправки, перешедшей из третьего полигона:
значение исходной невязки +37мм. изменится на величину поправки, перешедшей из третьего полигона:
WI’ = WI + VIII,I = 37 + (-12) = +25
Новую невязку так же распределяют по звеньям пропорционально красным числам и подписывают во внешних к полигону рамках под соответствующими красными числами.
Во втором полигоне новая невязка равна сумме начальной невязке и поправок, перешедших из третьего и первого полигонов.
WII’ = WII + VIII,II + VI,II = -17+ 5 +(-29) = -41
Полученную невязку распределяем так же по аналогии.
Приступаем ко второму циклу:
В третьем полигоне образуется новая невязка, равная сумме поправок, перешедших из смежных полигонов
WIII’ = VII,III + VI,III = -19 + 6 = -13
Невязку распределяем по аналогии.
В первом полигоне так же образуется новая поправка, равная сумме поправок смежных полигонов
WI’ = VIII,I + VII,I = -3 - 6 = -9
Далее по аналогии.
Циклы распределения продолжаются до тех пор, пока невязки всех полигонов не станут равными нулю.
Подсчитываем суммы чисел во всех рамках .
Контролем правильности распределения невязки служит равенство суммы чисел в рамочках поправок у внешних и внутренних звеньев и суммы чисел в рамочке невязок, соответствующего полигона.
+13 = +3+3+7
-54 = -25-8-21
-75= -40 -16 -19
Затем вычисляем поправки на звенья каждого полигона, считая направления звеньев совпадающими с направлением обхода полигона. При этом руководствуемся следующими правилами:

Для внешнего звена полигона поправка на звено равна сумме поправок внешней рамочки этого звена с обратным знаком. V1 = +7, V2 = +21, V3 = +19
Для звеньев смежных полигонов поправка равна разности сумм чисел внутренней и внешней табличек этого звена.
Для первого полигона: V1,2 = -8-3 = -11
V1,3 = -16-3 = -19
Для второго полигона: V2,1 = +3-(-8) = +11
V2,3 = -40-(-25) = -15
Для третьего полигона: V3,1 = +3-(-16) = +19
V3,2 = -25-(-40) = +15
Контролем уравнивания сети является выполнение условия: в каждом полигоне сумма поправок на звенья должна равняться невязке полигона с обратным знаком. Допуск 1мм.
-15 +21+11 = 17
15+19+19 = 53
-19-7-11 = -37
Оценка точности результатов уравнивания
| № | Длина хода,км | Р = C/L C= 30 | Поправка V,мм | 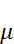 = = 
|
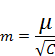
|
| АВ | 21,2 | 1,415 | -7 | СКО единицы веса = 36,31мм | СКО на 1 км хода = 6,63мм |
| ВС | 18,6 | 1,613 | +21 | ||
| СА | 9,6 | 3,125 | +19 | ||
| АД | 9,2 | 3,261 | +19 | ||
| ДС | 21,1 | 1,422 | +15 | ||
| ДВ | 6,6 | 4,545 | -11 |
Задача 4
|
из
5.00
|
Обсуждение в статье: Уравнивание нивелирной сети способом красных чисел ( Попова В.В.) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

