 |
Главная |
Тройной интеграл: определение, свойства
|
из
5.00
|
Пусть задано пространств. тело D. В точках этого тела определена ф-ция U=f(x,y,z). Разобьем это тело на конечное число Di –тых (i=1,2,3,…). В каждой области Di выберем произвол. точку (xi,yi,zi) и составим интегральную sn=S ò(xi,yi,zi) * DVi Если сущ. предел и он конечный и он не зависит от способа деления обл. D на части и выбора точек (xi,yi,zi) , то этот предел называют тройным интегралом по обл.D от ф-ции f(x,y,z) lim(l®0)sn=òòò f(x,y,z)dx dy dz Следовательно m=òòòR(x,y,z)dxdydz
Св-ва тройного интеграла аналогично св-м двойного интеграла 1) Всякая интегрируемая в обл. D ф-ция ограничена в этой области.
2) Могут быть построены суммы Дарбу
верх St=S Mi * DVi низ st=S mi * DVi
3) Необходимо и достаточное условие сущ. интеграла
lim(l®0)( St-st)=0
4) Как и в случае двойного интеграла сущ. тройной интеграл от любой непрерывной ф-ции, заданной в обл. D. Однако тройной интеграл сущ. и в случае, когда ф-ция f(x,y,z) имеет разрывы 1-го рода на конечном числе пов-тей данного тела D.
5)Тройной интеграл обладает св-вами линейности и аддетивности
òòòDfdx = òòòD1fdx + òòòD2 , где D=D1ÇD2
6)Если сущ. тройной интеграл от ф-ции f, то сущ. интеграл по модулю
и существует равенство
ôòòòô£ òòòôfôdv
Если функция fв области D ограничена какими-то числами m £ f £ М , то для тройного интеграла справидливо неравенство
mVd £òòò ¦dv£M VD
7) Имеет место теорема о среднем , т.е. если функция ¦(x,y,z) не-прерывная в области D , то справедливо равенство
òòò ¦dv = ¦ (X0 , Yo , Z0) (X0 , Yo , Z0)ÎD
45. Вычисление тройных интегралов
Определение: Тройным интегралом f(M) по обл. Ω ? R называется предел интегральной суммы
∑k=1nf(Mk)∆Vk = ∑k=1nf(ξk nk ζk)V(Ωk), если мелкость разбиения обл. Ω λ = max d(Ωk) стремится к 0.
Единственное отличие от ДИ заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.

Суммирование производится по области v, которая ограничена некоторой поверхностью j(x, y, z) = 0.

Здесь х1 и х2 – постоянные величины, у1 и у2 – могут быть некоторыми функциями от х или постоянными величинами, z1 и z2 – могут быть функциями от х и у или постоянными величинами.
Пример. Вычислить интеграл 


44 Замена переменной в двойном интеграле.Полярная система координат площ плоской фигуры
Расмотрим двойной интеграл вида  , где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х).
, где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х).
Положим х = f(u, v); y = j(u, v) Тогда dx =  ; dy =
; dy =  ;
; 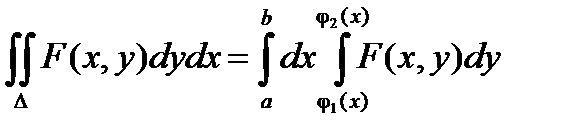 т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0. 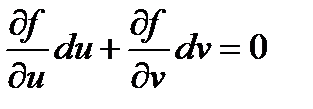 , т.е.
, т.е.  подставляя это выражение в записанное выше соотношение для dy, получаем:
подставляя это выражение в записанное выше соотношение для dy, получаем:  Выражение
Выражение  называется Якобианомфункций f(u, v) и j(u, v).
называется Якобианомфункций f(u, v) и j(u, v).
Тогда 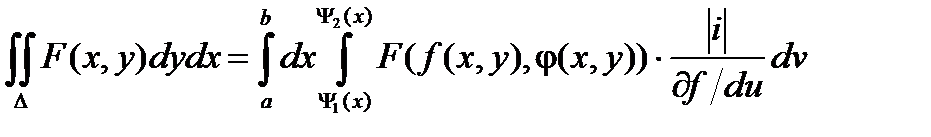 Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид
Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид  (при первом интегрировании v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:
(при первом интегрировании v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:

44Вычисление ДИ в полярной сист координат.  ,
, 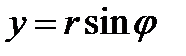



a) 
 b)
b) 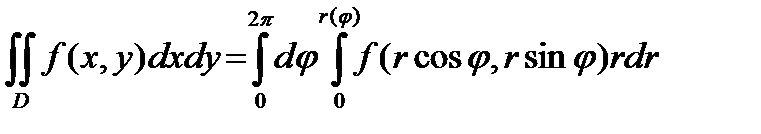
 c)
c) 
|
из
5.00
|
Обсуждение в статье: Тройной интеграл: определение, свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

