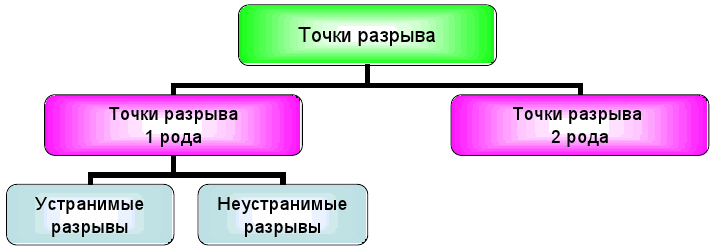
Определение непрерывности в точке функции. Точка разрыва функции и их классификация

43.Производная функции в точке.Уравнения касательной и нормали к графику функции.

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

44. Основные правила дифференцирования функций. Производная сложных функций.

Производная сложной функции ищется по следующему правилу:

(f(x(g(h)))`=f`(x)*x`(g)*g`(h)

45. Таблица производных элементарных функций.

46. Дифференциал функции. Производные и дифференциалы высших порядков.

47. Дифференцирование папраметрически заданных функций. Логарифмическое дифференцирование

параметрически заданные функции дифференцируются абсолютно также, как и обычные функции, такие как, например, у=х или у=sinx

ДЛЯ. ПРОВЕДЕНИЯ ЛОГАРИФМИЧЕСКОГО ДИФФЕРЕНЦИРОВАНИЯ НУЖНО ПРОЛОГАРИФМИРОВАТЬ ОБЕ ЧАСТИ УРАВНЕНИЯ У=F(X) В. ИТОГЕ ПРИДЕМ ВОТ В ТАКОМУ ДРУГУ- У'=У*LN F(X) ТУТ НАТУРАЛЬНЫЙ ЛОГАРИФМ

48. Основные теоремы о дифференцируемых функциях (теоремы Ролля, Лагранжа и
Коши).

1.Теорема Ролля:
фор-ка: Если функция f(x):
1) непрерывна на замкнутом промежутке [a,b];
2) дифференцируема в каждой точке интервала (a,b);
3) на концах отрезка принимает равные значения (f(a)=f(b)),
то тогда между точками a и b найдется хотя бы одна точка c (a<c<b) такая что f'(c)=0.

Геометрический смысл теоремы Ролля состоит в следующем:
Если выполнены условия теоремы Ролля, то в некоторой точке x = c
f '(c) = 0, а это означает, что внутри интервала всегда найдется точка
x = c, касательная к графику функции y = f (x) в которой параллельна
оси Ох.

2.Теорема Лагранжа.
Пусть функция y = f (x):
1) непрерывна на замкнутом промежутке [a, b],
2) дифференцируема на интервале (a, b) .
Тогда внутри промежутка [a, b] найдется хотя бы одна точка c
(a < c < b) такая, что будет иметь место равенство
f (b) - f (a) = f'(c)(b - a)– формула Лагранжа.

Геометрический смысл теоремы Лагранжа (см. рис1.)

3.Теорема Коши.
Пусть функции f(x) и g(x)
1) непрерывны на отрезке [a, b],
2) дифференцируемы в каждой точке интервала (a, b) ,
3) производная g'(x) не равна 0 ни в одной точке этого интервала.
Тогда между точками a и b существует такая точка c (a < c < b), что
имеет место равенство
f'(c)/g'(c)=(f(b)-f(a))/(g(b)-g(a))

49. Правило Лопиталя и раскрытие с его помощью всех видов неопределенностей.
Определение: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному).

Правило Лопиталя. Для раскрытия неопределенностей 0/0 бесконечность/бесконечность
надо заменить предел отношения двух функций пределом отношения их
производных. Если окажется, что отношение производных имеет
конечный предел, то к этому же пределу стремится и отношение
данных функций.
Если неопределенность не раскрылась после применения правила
Лопиталя, это правило можно применить еще раз, но уже к отношению
производных (при условии, что отношение производных f'(x)/g'(x)
порождает неопределенности 0/0 беск/беск
Н/п см. рис

50. Условие возрастания и убывания функций. Максимум и минимум функций. Достаточный признак существования экстремума функций.

1.Исследование функций с помощью первой производной
Признаки возрастания и убывания функции
Теорема. Пусть функция y=f(x) непрерывна на промежутке [a,b] и дифференцируема в каждой точке интервала (a, b).
F(x) –монотонно возрастает при f’(x)>0
F(x) – монотонно убывает при f’(x)<0

2.Экстремумы функции
Определение. Значение функции в точке x0 называется максимумом (минимумом) f(x), если существует такая окрестность точки x0, во всех точках которой выполняется условие f(x0)>f(x). (f(x0)<f(x)).

Точка x0 при этом называется точкой локального максимума (минимума).
Максимум или минимум функции обозначаются одним словом: экстремум.

Теорема (необходимое условие существование экстремума функции). Если функция f(x) дифференцируема в некоторой точке x0, принадлежащей интервалу (x0-(сигма); x0+(сигма)) и имеет в этой точке экстремум, то f’(x0)=0.

Замечание 1. Условие теоремы не является достаточным.
Замечание 2. Касательная к графику дифференцируемой функции в точке экстремума параллельна оси Ox .
Замечание 3. Экстремум может также существовать в точке, в которой производная не существует.

Определение. Точка x0 называется критической точкой первого рода функции y=f(x), если в этой точке производная функции равна нулю или не существует.
Определение. Критическая точка первого рода функции y=f(x), в которой производная равна нулю, называется стационарной точкой этой функции.
У функции может быть экстремум только в критических точках первого рода, поэтому иначе они называются точками, подозрительными на экстремум

Первый достаточный признак экстремума
Теорема. Если функция f (x) дифференцируема в некоторой окрестности точки x0 и производная f ‘(x) обращается в нуль в точке x0, то:
если при прохождении через точку x0 производная меняет знак “плюс” на “минус”, то в точке x0 функция имеет максимум;
если при прохождении через точку x0 производная меняет знак “минус” на “плюс”, то в точке x0 функция имеет минимум.

51.порядок нахождения наибольшего и наименьшего значений функции на отрезке

Пусть функция f (x) непрерывна на промежутке [a, b].
Тогда на этом промежутке она имеет наибольшее и наименьшее значения.
Для нахождения наибольшего и наименьшего значений непрерывной на промежутке [a, b] функции f(x) необходимо:
1) найти все критические точки функции на интервале (a, b),
2) вычислить её значения в этих точках,
3) найти значения функции на концах интервала,
4) из полученных значений выбрать наибольшее и наименьшее

52. Выпуклость и вогнутость графика функции. Точки перегиба графика. Достаточный признак существования перегиба.

Вторая производная. Если производная f ' ( x ) функции f ( x )дифференцируема в точке ( x₀ ), то её производная называетсявторой производной функции f ( x ) в точке ( x₀ ), и обозначаетсяf '' ( x₀ ).