 |
Главная |
Порядок выполнения работы. 1. Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и
|
из
5.00
|
1. Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х; оценить статистическую значимость коэффициентов корреляции r(Y, Xi); выбрать наиболее информативный фактор.
2. Построить модель парной регрессии с наиболее информативным фактором; дать экономическую интерпретацию коэффициента регрессии.
3. Оценить качество модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации и F – критерия Фишера (принять уровень значимости α=0,05).
4. С доверительной вероятностью γ=80% осуществить прогнозирование среднего значения показателя Y (прогнозные значения факторов приведены в Приложении 6). Представить графически фактические и модельные значения Y, результаты прогнозирования.
5. Методом включения построить двухфакторные модели, сохраняя в них наиболее информативный фактор; построить трехфакторную модель с полным перечнем факторов.
6. Выбрать лучшую из построенных множественных моделей. Дать экономическую интерпретацию ее коэффициентов.
7. Проверить значимость коэффициентов множественной регрессии с помощью t–критерия Стьюдента (принять уровень значимости α=0,05). Улучшилось ли качество множественной модели по сравнению с парной?
8. Дать оценку влияния факторов на результат с помощью коэффициентов эластичности, бета– и дельта– коэффициентов.
Задача 2. Моделирование одномерного временного ряда
В Приложении 7 приведены временные ряды Y(t) социально-экономических показателей по Алтайскому краю за период с 2000 г. по 2011 г. Требуется исследовать динамику показателя, соответствующего варианту задания.
| Вариант | Обозначение, наименование, единица измерения показателя | |
| Y1 | Потребительские расходы в среднем на душу населения (в месяц), руб. | |
| Y2 | Выбросы загрязняющих веществ в атмосферный воздух, тыс. тонн | |
| Y3 | Средние цены на вторичном рынке жилья (на конец года, за квадратный метр общей площади), руб | |
| Y4 | Объем платных услуг на душу населения, руб | |
| Y5 | Среднегодовая численность занятых в экономике, тыс. человек | |
| Y6 | Число собственных легковых автомобилей на 1000 человек населения (на конец года), штук | |
| Y7 | Среднедушевые денежные доходы (в месяц), руб | |
| Y8 | Индекс потребительских цен (декабрь к декабрю предыдущего года), % | |
| Y9 | Инвестиции в основной капитал (в фактически действовавших ценах), млн. руб | |
| Y10 | Оборот розничной торговли на душу населения (в фактически действовавших ценах), руб |
Порядок выполнения работы
1. Построить линейную модель временного ряда 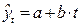 , параметры которой оценить МНК. Пояснить смысл коэффициента регрессии.
, параметры которой оценить МНК. Пояснить смысл коэффициента регрессии.
2. Оценить адекватность построенной модели, используя свойства случайности, независимости и соответствия остаточной компоненты нормальному закону распределения.
3. Оценить точность модели на основе использования средней относительной ошибки аппроксимации.
4. Осуществить прогнозирование рассматриваемого показателя на год вперед (прогнозный интервал рассчитать при доверительной вероятности 70%).
5. Представить графически фактические значения показателя, результаты моделирования и прогнозирования.
6. Провести расчет параметров логарифмического, полиномиального (полином 2-й степени), степенного, экспоненциального и гиперболического трендов. На основании графического изображения и значения индекса детерминации выбрать наиболее подходящий вид тренда.
7. С помощью лучшей нелинейной модели осуществить точечное прогнозирование рассматриваемого показателя на год вперед. Сопоставить полученный результат с доверительным прогнозным интервалом, построенным при использовании линейной модели.
ПРИМЕР
Выполнения контрольной работы
Задача 1
Фирма занимается реализацией подержанных автомобилей. Наименования показателей и исходные данные для эконометрического моделирования представлены в таблице:
| Цена реализации, тыс.у.е. (Y) | Цена нового авт., тыс.у.е. (Х1) | Срок эксплуатации, годы (Х2) | Левый руль - 1, правый руль - 0, (Х3) |
| 8,33 | 13,99 | 3,8 | |
| 10,40 | 19,05 | 2,4 | |
| 10,60 | 17,36 | 4,5 | |
| 16,58 | 25,00 | 3,5 | |
| 20,94 | 25,45 | 3,0 | |
| 19,13 | 31,81 | 3,5 | |
| 13,88 | 22,53 | 3,0 | |
| 8,80 | 16,24 | 5,0 | |
| 13,89 | 16,54 | 2,0 | |
| 11,03 | 19,04 | 4,5 | |
| 14,88 | 22,61 | 4,6 | |
| 20,43 | 27,56 | 4,0 | |
| 14,80 | 22,51 | 3,3 | |
| 26,05 | 31,75 | 2,3 |
Требуется:
1. Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х; оценить статистическую значимость коэффициентов корреляции r(Y, Xi); выбрать наиболее информативный фактор.
Используем Excel (Данные / Анализ данных / КОРРЕЛЯЦИЯ):
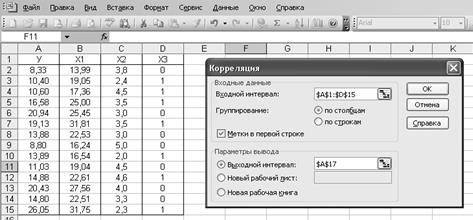
Получим матрицу коэффициентов парной корреляции между всеми имеющимися переменными:
| У | Х1 | Х2 | Х3 | |
| У | ||||
| Х1 | 0,910987 | |||
| Х2 | -0,4156 | -0,2603 | ||
| Х3 | 0,190785 | 0,221927 | -0,30308 |
Проанализируем коэффициенты корреляции между результирующим признаком Y и каждым из факторов Xj:
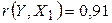 > 0, следовательно, между переменными Y и Х1 наблюдается прямая корреляционная зависимость: чем выше цена нового автомобиля, тем выше цена реализации.
> 0, следовательно, между переменными Y и Х1 наблюдается прямая корреляционная зависимость: чем выше цена нового автомобиля, тем выше цена реализации.
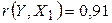 > 0,7 – эта зависимость является тесной.
> 0,7 – эта зависимость является тесной.
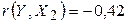 < 0, значит, между переменными Y и Х2 наблюдается
< 0, значит, между переменными Y и Х2 наблюдается
обратная корреляционная зависимость: цена реализации ниже для авто-
мобилей с большим сроком эксплуатации.
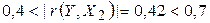 – эта зависимость умеренная, ближе к слабой.
– эта зависимость умеренная, ближе к слабой.
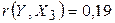 > 0, значит, между переменными Y и Х3 наблюдается прямая корреляционная зависимость: цена реализации выше для автомобилей с левым рулем.
> 0, значит, между переменными Y и Х3 наблюдается прямая корреляционная зависимость: цена реализации выше для автомобилей с левым рулем.
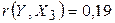 < 0,4 – эта зависимость слабая.
< 0,4 – эта зависимость слабая.
Для проверки значимости найденных коэффициентов корреляции используем критерий Стьюдента.
Для каждого коэффициента корреляции 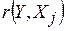 вычислим t-статистику по формуле
вычислим t-статистику по формуле 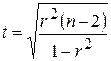 и занесем результаты расчетов в дополнительный столбец корреляционной таблицы:
и занесем результаты расчетов в дополнительный столбец корреляционной таблицы:
| У | Х1 | Х2 | Х3 | t-статистики | |
| У | |||||
| Х1 | 0,910987 | 7,651524603 | |||
| Х2 | -0,4156 | -0,2603 | 1,582847988 | ||
| Х3 | 0,190785 | 0,221927 | -0,30308 | 0,673265587 |
По таблице критических точек распределения Стъюдента при уровне значимости 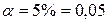 и числе степеней свободы
и числе степеней свободы 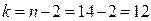 определим критическое значение
определим критическое значение 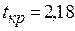 (Приложение 1, или функция СТЬЮДРАСПОБР).
(Приложение 1, или функция СТЬЮДРАСПОБР).
Сопоставим фактические значения t с критическим tkp, и сделаем выводы в соответствии со схемой:

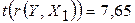 >
> 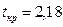 , следовательно, коэффициент
, следовательно, коэффициент 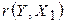 значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и Х1, зависимость цены реализации Y от цены нового автомобиля Х1 является достоверной.
значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и Х1, зависимость цены реализации Y от цены нового автомобиля Х1 является достоверной.
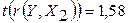 <
< 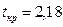 , следовательно, коэффициент
, следовательно, коэффициент 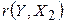 не является значимым. На основании выборочных данных нет оснований утверждать, что зависимость между ценой реализации Y и сроком эксплуатации Х2 достоверна.
не является значимым. На основании выборочных данных нет оснований утверждать, что зависимость между ценой реализации Y и сроком эксплуатации Х2 достоверна.
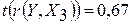 <
< 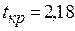 , следовательно, коэффициент
, следовательно, коэффициент 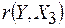 не является значимым. На основании выборочных данных нет оснований утверждать, что зависимость между ценой реализации Y и расположением руля Х3 достоверна.
не является значимым. На основании выборочных данных нет оснований утверждать, что зависимость между ценой реализации Y и расположением руля Х3 достоверна.
Таким образом, наиболее тесная и значимая зависимость наблюдается между ценой реализации Y и ценой нового автомобиля Х1; фактор Х1 является наиболее информативным.
|
из
5.00
|
Обсуждение в статье: Порядок выполнения работы. 1. Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

