 |
Главная |
Оценить точность модели на основе использования средней относительной ошибки аппроксимации
|
из
5.00
|
Используем исходные данные 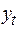 и найденные программой РЕГРЕССИЯ остатки
и найденные программой РЕГРЕССИЯ остатки 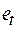 (таблица «Вывод остатка»). По формуле
(таблица «Вывод остатка»). По формуле 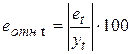 рассчитаем столбец относительных погрешностей и найдем среднее значение
рассчитаем столбец относительных погрешностей и найдем среднее значение 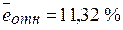 .
.
Сравнение показывает, что 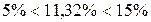 . Следовательно, точность модели удовлетворительная.
. Следовательно, точность модели удовлетворительная.
4. Осуществить прогнозирование цены на нефть на следующие 2 года (прогнозный интервал рассчитать при доверительной вероятности 90%).
«Следующие 2 года» соответствуют периодам упреждения 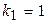 и
и 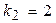 , при этом
, при этом 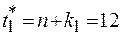 и
и 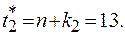
Согласно уравнению модели получим точечные прогнозные оценки
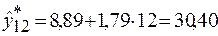 и
и 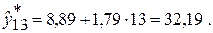
Таким образом, ожидаемые цены на нефть в следующие 2 года будут составлять около 30,40 долл. за баррель и 32,19 долл. за баррель соответственно.
Для оценки точности прогнозирования рассчитаем границы прогнозных интервалов для индивидуальных значений результирующего признака (доверительная вероятность 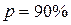 ).
).
Подготовим:
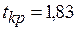 (функция СТЬЮДРАСПОБР при
(функция СТЬЮДРАСПОБР при 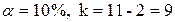 );
);
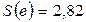 (строка «стандартная ошибка» итогов РЕГРЕССИИ);
(строка «стандартная ошибка» итогов РЕГРЕССИИ);
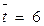 (функция СРЗНАЧ);
(функция СРЗНАЧ); 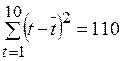 (функция КВАДРОТКЛ).
(функция КВАДРОТКЛ).
Вычислим размах прогнозного интервала для индивидуальных значений, используя формулу
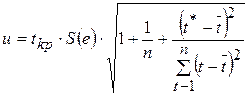 .
.
При 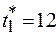 получим
получим 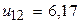 и определим границы доверительного интервала:
и определим границы доверительного интервала:
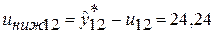 ;
; 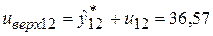 .
.
При 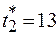 получим
получим 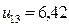 и определим границы доверительного интервала:
и определим границы доверительного интервала:
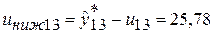 ;
; 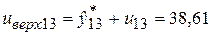 .
.
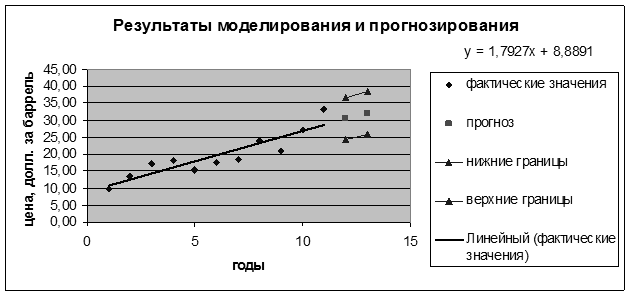
Таким образом, с надежностью 90% можно утверждать, что цены на нефть в следующем (12-ом) году будут составлять от 24,24 до 36,57 долл. за баррель, а через год (в 13-ом году) – от 25,78 до 38,61 долл. за баррель.
Представить графически фактические значения показателя, результаты моделирования и прогнозирования.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные.
Затем с помощью опции Добавить линию тренда… построим линию модели:
тип → линейная; параметры → показывать уравнение на диаграмме.
Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:
Имя → прогноз; значения Х → 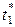 и
и 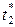 ; значения Y →
; значения Y → 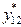 и
и 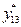 ;
;
Имя → нижние границы; значения Х → 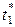 и
и 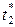 ; значения Y →
; значения Y → 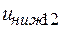 и
и 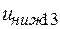 ;
;
Имя → верхние границы; значения Х → 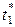 и
и 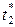 ; значения Y →
; значения Y → 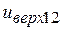 и
и 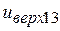 .
.
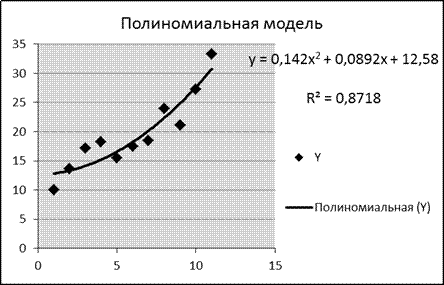
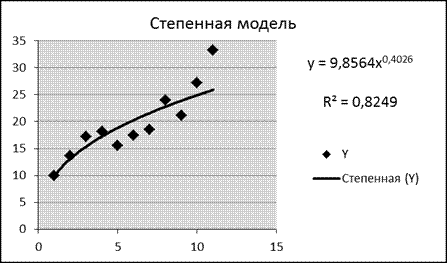
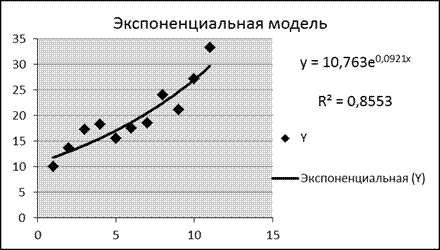
Провести расчет параметров логарифмического, полиномиального (полином 2-й степени), степенного, экспоненциального и гиперболического трендов. На основании графического изображения и значения индекса детерминации выбрать наиболее подходящий вид тренда.
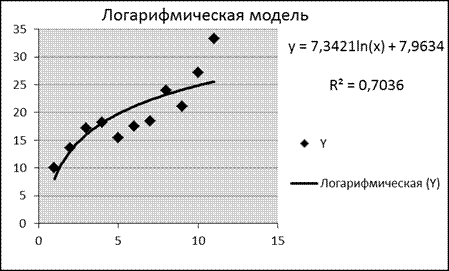
Логарифмическая, полиномиальная, степенная и экспоненциальная модели являются стандартными. Для их построения используем Мастер диаграмм: исходные данные покажем с помощью точечной диаграммы, затем добавим линию тренда соответствующего типа, выведем на диаграмму уравнение модели и величину достоверности аппроксимации (R2).
Гиперболическая модель 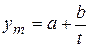 не является стандартной.
не является стандартной.
Для ее построения выполним линеаризацию: обозначим 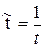 и получим вспомогательную модель
и получим вспомогательную модель 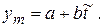 Вспомогательная модель является линейной. Ее можно построить с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные: столбец значений уi (остается без изменений) и столбец преобразованных значений
Вспомогательная модель является линейной. Ее можно построить с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные: столбец значений уi (остается без изменений) и столбец преобразованных значений 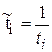 (таблица 7).
(таблица 7).
| Y | t | 1/t |
| 1,00 | ||
| 13,6 | 0,50 | |
| 17,2 | 0,33 | |
| 18,2 | 0,25 | |
| 15,5 | 0,20 | |
| 17,5 | 0,17 | |
| 18,5 | 0,14 | |
| 0,13 | ||
| 21,1 | 0,11 | |
| 27,2 | 0,10 | |
| 33,3 | 0,09 |
С помощью программы РЕГРЕССИЯ получим
| Коэффициенты | |
| Y-пересечение | 24,35011 |
| 1/t | -17,1369 |
Таким образом, 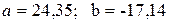 , следовательно, уравнение гиперболической модели
, следовательно, уравнение гиперболической модели 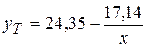 .
.
С помощью полученного уравнения рассчитаем теоретические значения 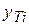 для каждого уровня исходных данных
для каждого уровня исходных данных 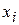 .
.
Покажем линию гиперболической модели на графике. Для этого добавим к ряду исходных данных 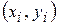 ряд теоретических значений
ряд теоретических значений 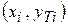 .
.
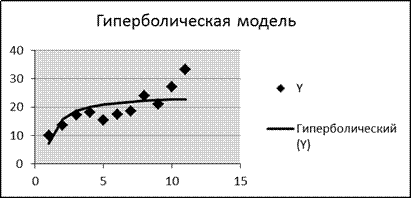
Индекс детерминации для гиперболической модели составляет 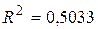 (итоги вспомогательной регрессии).
(итоги вспомогательной регрессии).
Сравнение графиков и значений индекса детерминации позволяет в качестве наиболее подходящей выбрать полиномиальную модель: 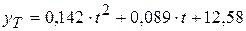 .
.
С помощью лучшей нелинейной модели осуществить точечное прогнозирование рассматриваемого показателя на следующие 2 года. Сопоставить полученные результаты с доверительными прогнозными интервалами, построенными при использовании линейной модели.
Рассчитаем по уравнению полиномиальной модели прогнозные значения показателя Y:
в следующем году 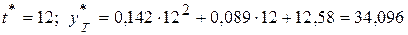 .
.
через год 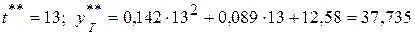 .
.
Полученные прогнозные оценки выше оценок, полученных при использовании линейной модели, однако попадают в доверительные прогнозные интервалы, построенные в п. 4. Это может служить подтверждением правильности прогноза, разработанного на основании линейной модели.
ВОПРОСЫ
|
из
5.00
|
Обсуждение в статье: Оценить точность модели на основе использования средней относительной ошибки аппроксимации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

