 |
Главная |
Выбрать лучшую из построенных множественных моделей. Дать экономическую интерпретацию ее коэффициентов
|
из
5.00
|
При добавлении в модель новых факторных переменных автоматически увеличивается коэффициент детерминации R2 и уменьшается средняя ошибка аппроксимации, хотя при этом не всегда улучшается качество модели. Поэтому для сравнения моделей с различным количеством учтенных в них факторов рассмотрим нормированные коэффициенты детерминации и стандартные ошибки моделей, которые приведены в таблице «Регрессионная статистика» итогов программы РЕГРЕССИЯ. Модель тем лучше, чем больше величина нормированного коэффициента детерминации и меньше величина ее стандартной ошибки.
| Модель | Нормированный R-квадрат | Стандартная ошибка |
 (2) (2)
| 0,839347 | 2,074288 |
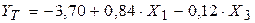 (3) (3)
| 0,799131 | 2,319424 |
 (4) (4)
| 0,828276 | 2,144569 |
Таким образом, лучшей является модель (2) зависимости цены реализации Y от цены нового автомобиля Х1 и срока эксплуатации Х2:  .
.
Коэффициент регрессии  , следовательно, при увеличении цены нового автомобиля (Х1) на 1 тыс.у.е. и неизменном сроке эксплуатации цена реализации (Y) увеличивается в среднем на 0,79 тыс.у.е.
, следовательно, при увеличении цены нового автомобиля (Х1) на 1 тыс.у.е. и неизменном сроке эксплуатации цена реализации (Y) увеличивается в среднем на 0,79 тыс.у.е.
Коэффициент регрессии  , следовательно, при увеличении срока эксплуатации (Х2) на 1 год и неизменной цене нового автомобиля цена реализации (Y) уменьшается в среднем на 1,07 тыс.у.е.
, следовательно, при увеличении срока эксплуатации (Х2) на 1 год и неизменной цене нового автомобиля цена реализации (Y) уменьшается в среднем на 1,07 тыс.у.е.
Свободный коэффициент не имеет экономического смысла.
7. Проверить значимость коэффициентов множественной регрессии с помощью t–критерия Стьюдента (принять уровень значимости α=0,05). Улучшилось ли качество множественной модели по сравнению с парной?
Значимость отдельных коэффициентов множественной модели (2) проверим с помощью t – критерия Стьюдента.
t – статистикидля коэффициентов уравнения регрессии приведены в итогах программы РЕГРЕССИЯ. Для выбранной модели (2) получены следующие значения:
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 1,074812 | 3,713112 | 0,289464 | 0,777609 |
| Х1 | 0,794224 | 0,106187 | 7,4795 | 1,23E-05 |
| Х2 | -1,066 | 0,641125 | -1,66271 | 0,124572 |
Критическое значение  найдено для уровня значимости a=5% и числа степеней свободы
найдено для уровня значимости a=5% и числа степеней свободы  (Приложение 1 или функция СТЬЮДРАСПОБР).
(Приложение 1 или функция СТЬЮДРАСПОБР).
Схема проверки: 
Для свободного коэффициента  определена статистика
определена статистика 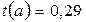 .
.
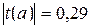 <
<  , следовательно, свободный коэффициент а не является значимым, его можно исключить из модели.
, следовательно, свободный коэффициент а не является значимым, его можно исключить из модели.
Для коэффициента регрессии  определена статистика
определена статистика 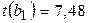 .
.
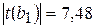 >
>  , значит, коэффициент регрессии b1 является значимым, его и фактор цены нового автомобиля нужно сохранить в модели.
, значит, коэффициент регрессии b1 является значимым, его и фактор цены нового автомобиля нужно сохранить в модели.
Для коэффициента регрессии  определена статистика
определена статистика  .
.
 <
<  , следовательно, коэффициент регрессии b2 не является значимым, его и фактор срока эксплуатации можно исключить из модели.
, следовательно, коэффициент регрессии b2 не является значимым, его и фактор срока эксплуатации можно исключить из модели.
Выводы о значимости коэффициентов модели сделаны на уровне значимости a=5%. Рассматривая столбец «Р-значение», отметим, что свободный коэффициент а можно считать значимым на уровне  ; коэффициент регрессии b1 – на уровне
; коэффициент регрессии b1 – на уровне  ; а коэффициент регрессии b2 – на уровне
; а коэффициент регрессии b2 – на уровне  .
.
Для сравнения качества парной модели (1) и выбранной множественной модели (2) используем нормированные коэффициенты детерминации и стандартные ошибки моделей.
| Модель | Нормированный R-квадрат | Стандартная ошибка |
 (1) (1)
| 0,815723 | 2,221571 |
 (2) (2)
| 0,839347 | 2,074288 |
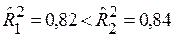 ;
;  ; таким образом, при добавлении в уравнение регрессии фактора «срок эксплуатации» Х2 качество модели улучшилось, что говорит в пользу сохранения фактора Х2 в модели.
; таким образом, при добавлении в уравнение регрессии фактора «срок эксплуатации» Х2 качество модели улучшилось, что говорит в пользу сохранения фактора Х2 в модели.
|
из
5.00
|
Обсуждение в статье: Выбрать лучшую из построенных множественных моделей. Дать экономическую интерпретацию ее коэффициентов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

