 |
Главная |
Базис векторного пространства и преобразование координат
|
из
5.00
|
Определение. Векторы 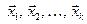 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство  возможно тогда и только тогда, когда все числа
возможно тогда и только тогда, когда все числа  равны нулю. В противном случае векторы
равны нулю. В противном случае векторы 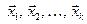 называются линейно зависимыми.
называются линейно зависимыми.
Определение. Система линейно независимых векторов  в пространстве
в пространстве  образует его базис, если
образует его базис, если  существует разложение
существует разложение
 ,
,
где  - элементы поля
- элементы поля  , над которым задано векторное пространство
, над которым задано векторное пространство  . Числа
. Числа  называются координатами вектора
называются координатами вектора  относительно базиса
относительно базиса  .
.
Теорема. Координаты вектора относительно заданного базиса определяются однозначно.
Отметим, что число базисных векторов определяет размерность векторного пространства.
Рассмотрим два базиса 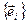 и
и  (штрихованный и не штрихованный) пространства
(штрихованный и не штрихованный) пространства  . Разложим один и тот же вектор относительно этих базисов
. Разложим один и тот же вектор относительно этих базисов
 ,
,
 .
.
(Здесь использовано обозначение Эйнштейна: если в формуле верхний и нижний индекс совпадает, то по этому индексу подразумевается суммирование). Видим, что при переходе к другому базису меняются координаты вектора (но не сам вектор!). Для нахождения формул преобразования координат, разложим векторы штрихованного базиса по не штрихованному базису
 ,
,
 ,
,
………………………..
 .
.
Определенная таким образом матрица

называется матрицей преобразования базиса  к базису
к базису 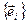 ( или матрицей перехода от базиса
( или матрицей перехода от базиса  к базису
к базису 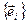 . Подставим формулу
. Подставим формулу  в разложение вектора
в разложение вектора  относительно штрихованного базиса
относительно штрихованного базиса
 .
.
Поскольку координаты вектора относительно базиса определяются однозначно, получаем  . Обратим это равенство. С этой целью умножим левую и правую части этого равенства на элементы новой матрицы
. Обратим это равенство. С этой целью умножим левую и правую части этого равенства на элементы новой матрицы  :
:  . «Свернем» это равенство по индексам
. «Свернем» это равенство по индексам  и
и  , т.е. приравняем их и возьмем сумму по единому индексу,
, т.е. приравняем их и возьмем сумму по единому индексу,  . Определим новую матрицу
. Определим новую матрицу  равенством
равенством  , где
, где  - символ Кронекера. Тогда
- символ Кронекера. Тогда  или
или  . Следовательно, координаты вектора преобразуются с помощью матрицы
. Следовательно, координаты вектора преобразуются с помощью матрицы  , являющейся обратной к матрице
, являющейся обратной к матрице 
Замечание. Образуем матрицы  ,
,  ,
,
 и
и  .
.
Формулы разложения вектора по базисам на матричном языке имеют вид  , а формулы преобразований базисов и координат записываются следующим образом
, а формулы преобразований базисов и координат записываются следующим образом  .
.
3.Гомоморфные и изоморфные отображения векторных пространств, линейные операторы, матрица оператора, собственные значения и собственные вектора оператора.
Определение. Пусть  и
и  - два векторных пространства. Отображение
- два векторных пространства. Отображение  называется гомеоморфным отображением или гомеоморфизмом, если оно сохраняет линейные операции, т.е. если выполняется равенство
называется гомеоморфным отображением или гомеоморфизмом, если оно сохраняет линейные операции, т.е. если выполняется равенство
 .
.
Определение. Взаимно однозначное гомоморфное отображение  называется изоморфным отображением или изоморфизмом. Если такое отображение
называется изоморфным отображением или изоморфизмом. Если такое отображение  существует, то пространства
существует, то пространства  и
и  называются изоморфными.
называются изоморфными.
Определение. Гомоморфное отображение  называется линейным оператором на пространстве
называется линейным оператором на пространстве  .
.
Множество линейных операторов на пространстве  можно превратить в векторное пространство, задав сумму операторов правилом
можно превратить в векторное пространство, задав сумму операторов правилом  и произведение оператора на число
и произведение оператора на число  . Каждому оператору можно поставить в соответствие матрицу, если выбрать некоторый базис
. Каждому оператору можно поставить в соответствие матрицу, если выбрать некоторый базис  пространства
пространства  . Подействуем оператором
. Подействуем оператором  на каждый базисный вектор и разложим получающиеся векторы по базису
на каждый базисный вектор и разложим получающиеся векторы по базису
 ,
,
 ,
,
…………………………
 .
.
Матрица

называется матрицей оператора  относительно базиса
относительно базиса  . При фиксированном базисе пространства
. При фиксированном базисе пространства  любая
любая  -матрица определяет оператор на этом пространстве. Действительно,
-матрица определяет оператор на этом пространстве. Действительно,
 ,
,
где  . Взаимно однозначное соответствие между операторами и их матрицами определяет изоморфизм между векторным пространством операторов и векторным пространством
. Взаимно однозначное соответствие между операторами и их матрицами определяет изоморфизм между векторным пространством операторов и векторным пространством  -матриц. Так как изоморфные пространства имеют одинаковую размерность, размерность векторного пространства операторов равна
-матриц. Так как изоморфные пространства имеют одинаковую размерность, размерность векторного пространства операторов равна  . При выборе другого базиса
. При выборе другого базиса  пространства
пространства  меняется матрица оператора (сам оператор не меняется, так как является вектором). Правило преобразования матрицы оператора имеет вид
меняется матрица оператора (сам оператор не меняется, так как является вектором). Правило преобразования матрицы оператора имеет вид  .
.
Определение. Вектор  называется собственным вектором оператора
называется собственным вектором оператора  , если
, если  , где
, где  называется собственным значением оператора
называется собственным значением оператора  .
.
4. Группы преобразований векторных пространств.
5.Сопряженные пространства, пространства билинейных функционалов.
Определение. Сопряженным (или дуальным, или двойственным)векторным пространством  к пространству
к пространству  называется векторное пространство линейных отображений (форм, функционалов)
называется векторное пространство линейных отображений (форм, функционалов)  таких, что
таких, что  . Сумма векторов в пространстве
. Сумма векторов в пространстве  вводится правилом
вводится правилом  , а умножение на число определяется следующим образом
, а умножение на число определяется следующим образом 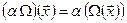 .
.
Определение. Отображение  называется билинейным функционалом на
называется билинейным функционалом на  , если при фиксированном значении одного аргумента оно является линейным функционалом относительно другого, т.е.
, если при фиксированном значении одного аргумента оно является линейным функционалом относительно другого, т.е.
 ,
,

 .
.
6. Скалярное произведение, вещественное евклидово пространство(скалярное произведение, неравенство Коши-Буняковского, ортонормированный базис, процедура ортогонализации)
Определение. Векторное пространство  с заданным на нем билинейным функционалом
с заданным на нем билинейным функционалом 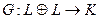 называется пространством со скалярным умножением. Значение (число)
называется пространством со скалярным умножением. Значение (число)  функционала
функционала  на векторе
на векторе  будем называть скалярным произведением векторов
будем называть скалярным произведением векторов  ,
,  и обозначать
и обозначать  .
.
Скалярное произведение в общем случае не обладает какой-либо симметрией. Выделим три случая:
1) 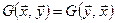 . Такие скалярные произведения называются симметричными и задаются симметричными матрицами
. Такие скалярные произведения называются симметричными и задаются симметричными матрицами  , где
, где  . Геометрия пространств с симметричным скалярным произведением называется ортогональной геометрией.
. Геометрия пространств с симметричным скалярным произведением называется ортогональной геометрией.
2) 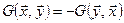 . Такие скалярные произведения называются антисимметричными (симплектическими) и задаются антисимметричными матрицами
. Такие скалярные произведения называются антисимметричными (симплектическими) и задаются антисимметричными матрицами  . Геометрия пространств с антисимметричным скалярным произведением называется симплектической геометрией.
. Геометрия пространств с антисимметричным скалярным произведением называется симплектической геометрией.
3)  . Такие скалярные произведения задаются матрицами, удовлетворяющими свойству
. Такие скалярные произведения задаются матрицами, удовлетворяющими свойству  , в векторных пространствах, определенных над полем комплексных чисел, и называются эрмитово-симметричными. В качестве примера можно привести скалярное произведение волновых функций в квантовой механике
, в векторных пространствах, определенных над полем комплексных чисел, и называются эрмитово-симметричными. В качестве примера можно привести скалярное произведение волновых функций в квантовой механике  .
.
Определение. Векторное пространство  с симметричным скалярным умножением, заданное над полем вещественных чисел
с симметричным скалярным умножением, заданное над полем вещественных чисел 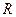 , называется евклидовым пространством, если
, называется евклидовым пространством, если  , причем равенство
, причем равенство  имеет место только в случае нулевого вектора
имеет место только в случае нулевого вектора  .
.
Замечание. Квадратичная форма  , обладающая отмеченным выше свойством, называется положительно определенной квадратичной формой.
, обладающая отмеченным выше свойством, называется положительно определенной квадратичной формой.
В евклидовом пространстве можно ввести норму (длину) вектора правилом  .
.
Теорема (неравенство Коши-Буняковского). Для любых двух векторов  и
и  евклидового пространства справедливо неравенство
евклидового пространства справедливо неравенство
 .
.
Следствие (неравенство треугольника). Для любых двух векторов  и
и  евклидового пространства справедливо неравенство
евклидового пространства справедливо неравенство
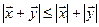 .
.
Справедливость неравенства Коши-Буняковского для евклидовых пространств позволяет ввести для этих пространств понятие угла  между векторами с помощью формулы
между векторами с помощью формулы
 .
.
В общем случае два вектора пространства  со скалярным умножением
со скалярным умножением  называются ортогональными, если их скалярное произведение
называются ортогональными, если их скалярное произведение  равно нулю. В евклидовых пространствах угол между ортогональными векторами равен
равно нулю. В евклидовых пространствах угол между ортогональными векторами равен  (т.е. такие векторы перпендикулярны).
(т.е. такие векторы перпендикулярны).
Определение. Будем говорить, что  элементов
элементов 
 -мерного евклидового пространства образует ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если
-мерного евклидового пространства образует ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если  .
.
Теорема. Во всяком евклидовом пространстве  существует ортонормированный базис.
существует ортонормированный базис.
Доказательство этой теоремы заключается в построении такого базиса. Пусть  - некоторый базис пространства
- некоторый базис пространства  . Ортонормированным базисом
. Ортонормированным базисом  будет базис:
будет базис:
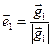 , где
, где  ;
;
 , где
, где  ;
;
 , где
, где  ;
;
………………………………………..
 , где
, где 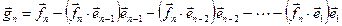 .
.
Отметим два основных свойства ортонормированных базисов.
Свойство 1. При использовании ортонормированного базиса скалярное произведение любых двух векторов равно сумме произведений их соответствующих координат.
Действительно,  .
.
Свойство 2. Координаты произвольного вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы.
Действительно, 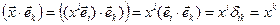
Понятие тензора
Определение. Тензором типа  валентности
валентности  называется объект, который задается в некоторой системе координат
называется объект, который задается в некоторой системе координат  набором чисел
набором чисел  , преобразующихся по тензорному закону
, преобразующихся по тензорному закону
 ,
,
при замене системы координат  .
.
В соответствии с определением вектор  является тензором типа
является тензором типа  , а ковектор
, а ковектор  - тензором типа
- тензором типа  . Оба имеют валентность, равную единице.
. Оба имеют валентность, равную единице.
Можно определить различные операции над тензорами.
1. Сложение тензоров:  (
(  .
.
2. Умножение тензора на число: 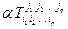 (
(  ).
).
3. Свертка тензора: 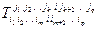 (по индексу
(по индексу  проводится суммирование).
проводится суммирование).
4. Тензорное умножение:  (
(  ).
).
Индексы тензора можно поднимать и опускать. Введем метрический тензор  . С помощью этого тензора можно опускать индексы:
. С помощью этого тензора можно опускать индексы:  . Числа
. Числа  называются ковариантными координатами вектора, а числа
называются ковариантными координатами вектора, а числа  - контрвариантными координатами вектора
- контрвариантными координатами вектора  . С помощью тензора
. С помощью тензора  индексы тензора можно поднимать:
индексы тензора можно поднимать:  . Матрицы
. Матрицы  и
и 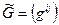 связаны соотношением
связаны соотношением  (для симметричных скалярных произведений).
(для симметричных скалярных произведений).
|
из
5.00
|
Обсуждение в статье: Базис векторного пространства и преобразование координат |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

