 |
Главная |
Линейные уравнения n-го порядка с постоянными коэффициентами
|
из
5.00
|
I. Определение. Линейным однородным дифференциальным уравнением  -го порядка с постоянными коэффициентами называется уравнение вида
-го порядка с постоянными коэффициентами называется уравнение вида  , (1)
, (1)
где  - постоянные величины.
- постоянные величины.
Система функций 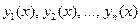 называется линейно независимой на интервале
называется линейно независимой на интервале 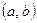 , если равенство
, если равенство  , где
, где  , выполняется тогда и только тогда, когда все коэффициенты
, выполняется тогда и только тогда, когда все коэффициенты 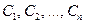 равны нулю. В противном случае она является линейно зависимой.
равны нулю. В противном случае она является линейно зависимой.
Совокупность любых  линейно независимых на интервале
линейно независимых на интервале 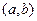 частных решений уравнения (1) определяет фундаментальную систему решений этого уравнения.
частных решений уравнения (1) определяет фундаментальную систему решений этого уравнения.
Теорема. Если  частных решений
частных решений  ,
,  уравнения (1) образуют на интервале
уравнения (1) образуют на интервале 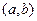 фундаментальную систему решений, то общим решением этого уравнения является функция
фундаментальную систему решений, то общим решением этого уравнения является функция  , где
, где  - произвольные постоянные.
- произвольные постоянные.
Частные решения уравнения (1) можно искать в виде  , где постоянные величины
, где постоянные величины  являются корнями характеристического уравнения
являются корнями характеристического уравнения
 . (2)
. (2)
При составлении фундаментальной системы решений уравнения (1) следует руководствоваться правилами:
1) каждому однократному действительному корню  характеристического уравнения (2) соответствует фундаментальное решение
характеристического уравнения (2) соответствует фундаментальное решение 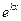 ;
;
2) каждому действительному корню  кратности
кратности  соответствуют
соответствуют  фундаментальных решений
фундаментальных решений  ;
;
3) каждой паре комплексно сопряженных однократных корней 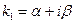 и
и  соответствуют два фундаментальных решения
соответствуют два фундаментальных решения  и
и  ;
;
4) каждой паре комплексно сопряженных корней 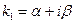 ,
,  кратности
кратности  соответствуют
соответствуют  фундаментальных решений
фундаментальных решений
 ,
,
 .
.
II. Определение. Линейным неоднородным дифференциальным уравнением  -го порядка с постоянными коэффициентами называется уравнение вида
-го порядка с постоянными коэффициентами называется уравнение вида 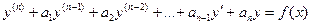 , (3)
, (3)
где  - постоянные величины,
- постоянные величины, 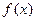 - непрерывная функция.
- непрерывная функция.
Теорема. Если  - общее решение однородного уравнения (1), а
- общее решение однородного уравнения (1), а  - частное решение неоднородного уравнения (3), то функция
- частное решение неоднородного уравнения (3), то функция  - общее решение уравнения (3).
- общее решение уравнения (3).
В некоторых специальных случаях есть некоторые правила поиска частного решения  (метод неопределенных коэффициентов).
(метод неопределенных коэффициентов).
Случай 1.  , где
, где  - многочлен степени
- многочлен степени  .
.
А. Если  не является корнем характеристического уравнения (2), то частное решение
не является корнем характеристического уравнения (2), то частное решение  следует искать в вид
следует искать в вид  , где
, где  - многочлен n-ой степени с произвольными коэффициентами.
- многочлен n-ой степени с произвольными коэффициентами.
Б. Если  - корень уравнения (2) кратности
- корень уравнения (2) кратности  , то частное решение
, то частное решение  ищут в виде
ищут в виде 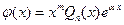 .
.
Случай 2.  .
.
А. Если числа  не являются корнями характеристического уравнения (2), то частное решение
не являются корнями характеристического уравнения (2), то частное решение  следует искать в виде
следует искать в виде
 ,
,
где  и
и  - произвольные постоянные.
- произвольные постоянные.
Б. Если числа  являются корнями характеристического уравнения (2) кратности
являются корнями характеристического уравнения (2) кратности  , то частное решение
, то частное решение  ищут в виде
ищут в виде
 .
.
Замечание. В случаях  или
или  частное решение по-прежнему следует искать в указанном полном виде.
частное решение по-прежнему следует искать в указанном полном виде.
Случай 3.  , где
, где  и
и  - многочлены степени m и n, соответственно.
- многочлены степени m и n, соответственно.
А. Если  не являются корнями характеристического уравнения (2), то частное решение
не являются корнями характеристического уравнения (2), то частное решение  следует искать в виде
следует искать в виде
 ,
,
где  и
и  - многочлены с произвольными коэффициентами степени
- многочлены с произвольными коэффициентами степени  .
.
Б. Если  являются корнями характеристического уравнения (2) кратности
являются корнями характеристического уравнения (2) кратности  , то частное решение
, то частное решение  ищут в виде
ищут в виде
 .
.
Для нахождения частного решения уравнения (3) в общем случае можно воспользоваться методом вариации постоянных (методом Лагранжа).
Рассмотрим общее решение однородного уравнения
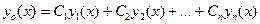 .
.
Частное решение неоднородного уравнения (3) ищется в виде
 ,
,
где  ,
,  , …
, …  - дифференцируемые функции, которые находятся путем решения системы дифференциальных уравнений
- дифференцируемые функции, которые находятся путем решения системы дифференциальных уравнений

Эта система имеет единственное решение для функций  ,
,  , …
, …  , поскольку в силу линейной независимости фундаментальных решений
, поскольку в силу линейной независимости фундаментальных решений 
вронскиан

не равен нулю.
Замечание. Пусть мы имеем уравнение 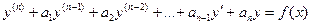 , где
, где  . Если функции
. Если функции  и
и  являются решениями соответственно уравнений
являются решениями соответственно уравнений  и
и  , то функция
, то функция  - решение уравнения
- решение уравнения 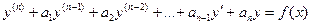 .
.
|
из
5.00
|
Обсуждение в статье: Линейные уравнения n-го порядка с постоянными коэффициентами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

