 |
Главная |
Степенные ряды(понятие степенного ряда, теорема Абеля, интервал и радиус сходимости ряда)
|
из
5.00
|
Частным случаем функциональных рядов являются степенные ряды, имеющие вид
 , (3)
, (3)
где 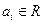 - коэффициенты степенного ряда. Заметим, что степенные ряды более общего вида
- коэффициенты степенного ряда. Заметим, что степенные ряды более общего вида
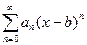 (4)
(4)
где 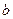 - некоторое число, с помощью простой замены
- некоторое число, с помощью простой замены  приводится к ряду (3). Очевидно, что точка
приводится к ряду (3). Очевидно, что точка  является точкой сходимости степенного ряда (3).
является точкой сходимости степенного ряда (3).
Теорема Абеля. 1. Если степенной ряд сходится при 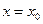 , не равном нулю, то он абсолютно сходится при всех
, не равном нулю, то он абсолютно сходится при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 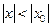 . 2. Если степенной ряд расходится при
. 2. Если степенной ряд расходится при 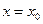 , то он расходится при всех
, то он расходится при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 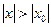 .
.
Из этой теоремы следует, что если 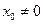 , то во всех точках интервала
, то во всех точках интервала 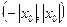 степенной ряд сходится абсолютно, вне этого интервала ряд расходится. Положим
степенной ряд сходится абсолютно, вне этого интервала ряд расходится. Положим  . Интервал
. Интервал  называется интервалом сходимости степенного ряда (3), а число
называется интервалом сходимости степенного ряда (3), а число 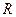 - радиусом сходимости этого ряда. Если степенной ряд сходится в единственной точке
- радиусом сходимости этого ряда. Если степенной ряд сходится в единственной точке  , то считается, что
, то считается, что  ; если же степенной ряд сходится во всех точках числовой оси, то
; если же степенной ряд сходится во всех точках числовой оси, то 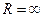 .
.
Замечание 5. На концах интервала (  ) сходимость ряда в каждом случае исследуется отдельно.
) сходимость ряда в каждом случае исследуется отдельно.
Замечание 6. Если рассматривается степенной ряд общего вида (4), то интервал сходимости имеет вид 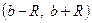 .
.
Свойства степенных рядов.
Свойство 1. Степенной ряд, составленный из производных членов ряда (3), имеет тот же радиус сходимости, что и сам ряд (3).
Свойство 2. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.
Свойство 3. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз.
Свойство 4. Степенной ряд можно почленно интегрировать в интервале сходимости.
Свойство 5. Радиус сходимости степенного ряда (3) можно найти по формулам:  (следствие признака Даламбера) и
(следствие признака Даламбера) и 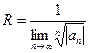
Разложение функций в степенные ряды. Ряд Тейлора и Маклорена.
Определения. Пусть функция 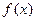 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 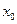 производные до
производные до 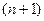 -го порядка включительно, тогда для любой точки
-го порядка включительно, тогда для любой точки  , принадлежащей этой окрестности, справедлива формула Тейлора
, принадлежащей этой окрестности, справедлива формула Тейлора
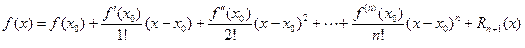 , (1)
, (1)
где функция 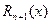 называется остаточным членом. Эта функция может быть записана в разных видах:
называется остаточным членом. Эта функция может быть записана в разных видах:
1) остаточный член в форме Коши
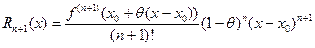 ,
,
где 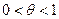 ;
;
2) остаточный член в форме Лагранжа
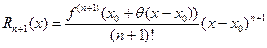 ,
,
где 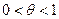 ;
;
3) остаточный член в форме Пеано
 ,
,
где символ «о» («о малое») означает, что 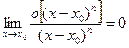 .
.
В случае  формула
формула

называется формулой Маклорена.
Если функция 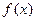 имеет производные любых порядков в окрестности точки
имеет производные любых порядков в окрестности точки 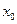 и остаточный член
и остаточный член 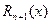 стремится к нулю при
стремится к нулю при 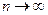 (т.е.
(т.е.  ), то формула Тейлора приводит к разложению функции
), то формула Тейлора приводит к разложению функции 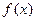 в степенной ряд
в степенной ряд
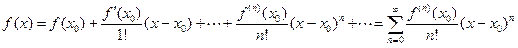 , (2)
, (2)
называемый рядом Тейлора. Степенной ряд
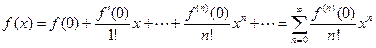
называется рядом Маклорена.
Ряды Маклорена следующих функций
 ,
, 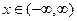 ,
,
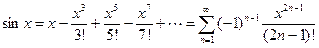 ,
, 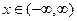 ,
,
 ,
,
 ,
, 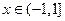 ,
,

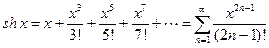 ,
, 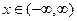 ,
,
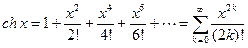
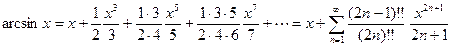 ,
,  ,
,
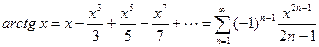 ,
,  ,
,
|
из
5.00
|
Обсуждение в статье: Степенные ряды(понятие степенного ряда, теорема Абеля, интервал и радиус сходимости ряда) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

