 |
Главная |
Как решить линейное уравнение?
|
из
5.00
|
Существуют два способа решения. Первый способ – это так называемый метод вариации произвольной постоянной, если вас интересует именно он, пожалуйста, перейдите по ссылке. Второй способ связан с заменой переменной и подстановкой, иногда его называют методом Бернулли. В данной статье будет рассматриваться метод подстановки, он алгоритмически прост и понятен, и решение уравнения принимает чёткий трафаретный характер. Рекомендую начинающим.
В который раз у меня хорошая новость! Линейное дифференциальное уравнение можно решить одной-единственной заменой:
 , где
, где 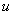 и
и  – некоторые, пока ещё неизвестные функции, зависящие от «икс».
– некоторые, пока ещё неизвестные функции, зависящие от «икс».
Коль скоро проводится замена  , то нужно выяснить, чему равна производная. По правилу дифференцирования произведения:
, то нужно выяснить, чему равна производная. По правилу дифференцирования произведения: 
Подставляем  и
и  в наше уравнение
в наше уравнение  :
:

В чём состоит задача? Необходимо найти неизвестные функции «у» и «вэ», которые зависят от «икс». И как раз этому будут посвящены все последующие действия.
После подстановки смотрим на два слагаемых, которые располагаются вот на этих местах:

У них нужно вынести за скобки всё, что можно вынести. В данном случае:

Теперь нужно составить систему уравнений. Система составляется стандартно:
Приравниваем к нулю то, что находится в скобках: 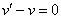 .
.
Если 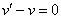 , тогда из нашего уравнения
, тогда из нашего уравнения  получаем:
получаем: 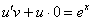 или просто
или просто  .
.
Уравнения записываем в систему:
 .
.
Именно в таком порядке.
Система опять же решается стандартно.
Сначала из первого уравнения находим функцию  . Это простейшее уравнение с разделяющимися переменными, поэтому его решение я приведу без комментариев.
. Это простейшее уравнение с разделяющимися переменными, поэтому его решение я приведу без комментариев.

Функция  найдена. Обратите внимание, что константу
найдена. Обратите внимание, что константу 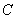 на данном этапе мы не приписываем.
на данном этапе мы не приписываем.
Далее подставляем найденную функцию 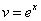 во второе уравнение системы
во второе уравнение системы  :
:

Да тут ништяк, экспоненты сокращаются, и получается диффур, даже не простейший, а для студенток муз-педа.
Из второго уравнения находим функцию 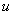 .
.


Функция 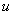 найдена. А вот здесь уже добавляем константу
найдена. А вот здесь уже добавляем константу 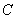 .
.
Ха. А задача-то решена! Вспоминаем, с чего всё начиналось:  .
.
Обе функции найдены:
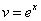
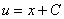
Записываем общее решение:
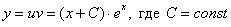
В ответе можно раскрыть скобки, это дело вкуса:
Ответ: общее решение 
Проверка выполняется по той же технологии, которую мы рассматривали на уроке Дифференциальные уравнения первого порядка.
Берём полученный ответ 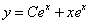 и находим производную:
и находим производную:

Подставим  и
и  в исходное уравнение
в исходное уравнение  :
:

Получено верное равенство, таким образом, общее решение найдено правильно.
Пример 2
Найти общее решение дифференциального уравнения 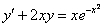
Решение: Данное уравнение имеет «классический» вид 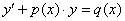 линейного уравнения. Проведем замену:
линейного уравнения. Проведем замену: 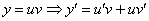 и подставим
и подставим  и
и  в исходное уравнение
в исходное уравнение 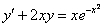 :
:
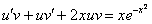
После подстановки проведем вынесение множителя за скобки, какие два слагаемых нужно мучить – смотрите предыдущий пример. Хотя, наверное, все уже поняли:

Составляем систему. Для этого приравниванием к нулю то, что находится в скобках:  , автоматически получая и второе уравнение системы:
, автоматически получая и второе уравнение системы:
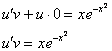
В результате:
 .
.
Из первого уравнения найдем функцию  :
:

 – найденную функцию
– найденную функцию  подставим во второе уравнение системы
подставим во второе уравнение системы  :
:

Теперь находим функцию 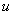 . Уравнение опять получилось простенькое:
. Уравнение опять получилось простенькое:


Обе функции найдены:

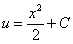
Таким образом:
Общее решение: 
Ответ: общее решение: 
Желающие могут выполнить проверку, для проверки в ответе лучше предварительно раскрыть скобки.
Пример 3
Найти общее решение дифференциального уравнения 
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Если у вас возникли (или возникнут) проблемы технического характера, пожалуйста, вернитесь к первому уроку Дифференциальные уравнения первого порядка.
Как видите, алгоритм решения линейного уравнения довольно прост. В чем особенность решения линейных уравнений? Особенность состоит в том, что практически всегда в ответе получается общее решение, в отличие, например, от однородных уравнений, где общее решение хорошо выражается крайне редко и ответ приходится записывать в виде общего интеграла.
Рассмотрим что-нибудь с дробями
Пример 4
Найти частное решение дифференциального уравнения 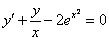 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 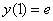
Напоминаю, что такая постановка вопроса также называется задачей Коши.
Решение: Алгоритм решения полностью сохраняется, за исключением того, что в конце прибавится один небольшой пунктик.
Обратите внимание, что уравнение представлено не совсем в стандартной форме. Этого в данном случае можно не делать, но я все-таки рекомендую всегда переписывать уравнения в привычном виде 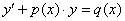 :
:

Данное ДУ является линейным, проведем замену: 
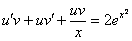
Типовой вынос за скобки:

Составим и решим систему:

Из первого уравнения найдем  :
:

 – подставим найденную функцию во второе уравнение системы и найдем функцию
– подставим найденную функцию во второе уравнение системы и найдем функцию 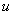 :
:

Здесь интеграл взят методом подведения функции под знак дифференциала.
Обе функции найдены, таким образом, общее решение:

На заключительном этапе нужно решить задачу Коши, то есть найти частное решение, удовлетворяющее начальному условию 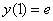 . Как находить частное решения для диффура первого порядка, мы очень подробно рассмотрели на уроке Дифференциальные уравнения первого порядка.
. Как находить частное решения для диффура первого порядка, мы очень подробно рассмотрели на уроке Дифференциальные уравнения первого порядка.
В данном случае:

Ответ: частное решение: 
А вот проверку частного решения еще раз повторим. Сначала проверяем, действительно ли выполняется начальное условие 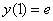 ?
?
 – да, начальное условие выполнено.
– да, начальное условие выполнено.
Теперь берём полученный ответ  и находим производную. Используем правило дифференцирования частного:
и находим производную. Используем правило дифференцирования частного:

Подставим  и
и  в исходное уравнение
в исходное уравнение 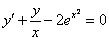 :
:

Получено верное равенство, значит, задание выполнено верно.
Пример 5
Найти решение задачи Коши
 ,
, 
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Перейдем к рассмотрению «частных видов» линейных уравнений, о которых шла речь в начале урока.
Пример 6
Найти решение задачи Коши для данного дифференциального уравнения
 ,
, 
Решение:В данном уравнении слагаемые опять не на своих местах, поэтому сначала пытаемся максимально близко приблизить диффур к виду 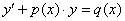 :
:

Что здесь особенного? Во-первых, в правой части у нас константа  . Это допустимо. Во-вторых, рядом с производной есть множитель
. Это допустимо. Во-вторых, рядом с производной есть множитель 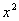 , который зависит только от «икс». Это тоже допустимо. Из-за этих особенностей линейное уравнение не перестает быть линейным.
, который зависит только от «икс». Это тоже допустимо. Из-за этих особенностей линейное уравнение не перестает быть линейным.
Алгоритм решения полностью сохраняется за исключением пары нюансов в самом начале.
Проведем замену: 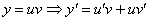
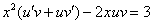
Теперь следовало бы выполнить вынесение множителя за скобки. Прозвучит каламбурно, но сначала нам нужно раскрыть скобку, поскольку одно из нужных нам слагаемых недоступно:
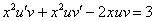
Вот теперь проводим вынесение множителя скобки:
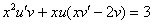
Обратите внимание на тот факт, что за скобки мы вынесли не только функцию 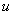 , но еще и «икс». Всё,что можно вынести за скобки – выносим.
, но еще и «икс». Всё,что можно вынести за скобки – выносим.
Составим и решим систему:
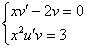
Из первого уравнения найдем  :
:

 – подставим во второе уравнение системы:
– подставим во второе уравнение системы:
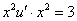


Таким образом, общее решение:

Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение: 
Пример 7
Найти частное решение ДУ
 ,
, 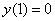
Это пример для самостоятельного решения.
Какие трудности встречаются в ходе решения линейного уравнения? Основной камень преткновения состоит в том, что может появиться довольно сложный интеграл. Как правило, неприятный интеграл появляется при нахождении функции 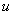 (в то время как с нахождением функции
(в то время как с нахождением функции  обычно проблем не возникает).
обычно проблем не возникает).
Рассмотрим пару примеров с такими интегралами.
Пример 8
Найти общее решение ДУ
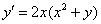
Решение: Сначала приводим линейное уравнение к родному виду 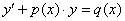 :
:


Уравнение кажется простым, но, как я уже отмечал, впечатление может быть обманчивым. Не редкость, когда «страшный» диффур на самом деле оказывается несложным, а «легкий» на вид диффур вызывает мучительную боль за бесцельно прожитые часы.
Проведем замену: 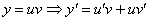


Составим и решим систему:
 .
.
Из первого уравнения найдем  :
:

 – подставим найденную функцию во второе уравнение:
– подставим найденную функцию во второе уравнение:


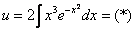
Такой интеграл, кстати, еще нигде не встречался в моих уроках. Он берется по частям. Вспоминаем формулу интегрирования по частям:  . Но, вот незадача, буквы
. Но, вот незадача, буквы 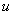 и
и  у нас уже заняты, и использовать те же самые буквы в формуле – не есть хорошо. Что делать? Используем ту же формулу, но с другими буквенными обозначениями. Можно выбрать любые другие буквы, я привык записывать правило с «а» и «бэ»:
у нас уже заняты, и использовать те же самые буквы в формуле – не есть хорошо. Что делать? Используем ту же формулу, но с другими буквенными обозначениями. Можно выбрать любые другие буквы, я привык записывать правило с «а» и «бэ»:
Интегрируем по частям:
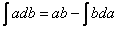

Если возникли трудности или недопонимание, освежите знания на уроках Метод замены переменной и Интегрирование по частям.
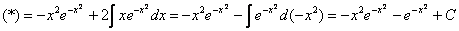
Таким образом:

Ответ: общее решение: 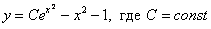
Давненько я не вспоминал интегрирование по частям, даже ностальгия появилась. А поэтому еще один пример для самостоятельного решения. Какой пример? Конечно же, с логарифмом! Ну а чего еще от меня можно было ожидать? =)
Пример 9
Найти общее решение дифференциального уравнения

В предложенном примере проявлена небольшая вольность для любознательных фанатов матана. Нет, алгоритм остался точно таким же, просто я сразу начал решать диффур, не перенеся предварительно  в правую часть. Полное решение и ответ в конце урока.
в правую часть. Полное решение и ответ в конце урока.
В моей коллекции есть уравнения и с более трудными интегралами, но сейчас речь идет о дифференциальных уравнениях. В этой связи я намеренно не включил в урок такие задачи, все-таки интегралы изучаются в другой теме.
Надеюсь, мои примеры и объяснения были полезны, до скорых встреч!
Решения и ответы:
Пример 3: Решение: Данное уравнение является линейным неоднородным, проведем замену: 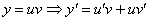


Составим и решим систему:
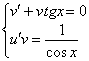
Из первого уравнения найдем  :
:




 – подставим во второе уравнение системы:
– подставим во второе уравнение системы:


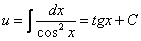
Таким образом: 
Ответ: общее решение: 
Пример 5: Решение: Данное уравнение является линейным неоднородным, замена: 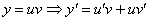

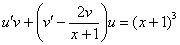
Составим и решим систему:
 .
.
Из первого уравнения найдем  :
:
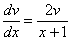


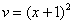 – подставим во второе уравнение системы:
– подставим во второе уравнение системы:
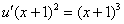


Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение: 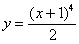
Пример 7: Решение: Данное уравнение является линейным неоднородным, замена: 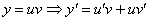


(раскрыли только левые скобки!)
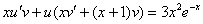
Составим и решим систему:
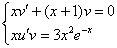 .
.
Из первого уравнения найдем  :
:

 – подставим во второе уравнение:
– подставим во второе уравнение:
(Примечание: здесь использовано основное логарифмическое тождество: 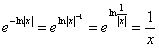 ).
).

Таким образом, общее решение:
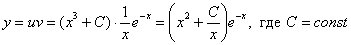
Найдем частное, соответствующее заданному начальному условию:

Ответ: частное решение: 
Пример 9: Решение: Данное ДУ является линейным, проведем замену: 


Решим систему:

Из первого уравнения найдем  :
:


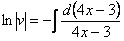


 – подставим во второе уравнение:
– подставим во второе уравнение:

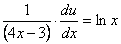
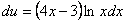

Интегрируем по частям:


Таким образом: 
Ответ: общее решение: 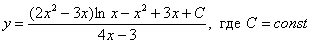
Дифференциальные уравнения в полных дифференциалах.
Примеры решений
Помимо дифференциальных уравнений с разделяющимися переменными, однородных уравнений и линейных неоднородных уравнений первого порядка, в практических задачах время от времени встречаются так называемые уравнения в полных дифференциалах. Да, конечно, ДУ в полных дифференциалах не такой частый гость в контрольных заданиях. Но освоить этот вид уравнений крайне важно, так как приёмы решения, о которых пойдет речь на данном уроке, потребуются при вычислении двойных, тройных, криволинейных интегралов, а также в ряде задач комплексного анализа.
Дифференциальные уравнения в полных дифференциалах – вещь довольно простая, вы даже удивитесь, насколько прозрачен и доступен алгоритм решения. Что необходимо знать, для того чтобы разобраться в этих диффурах? Во-первых, нужно ориентироваться в базовых понятиях темы, ответьте прямо сейчас на несколько простейших вопросов:
– Что такое дифференциальное уравнение?
– Что значит решить дифференциальное уравнение?
– Что такое общее решение, общий интеграл, частное решение?
В том случае, если возникло малейшее недопонимание терминов, или вы недавно столкнулись с диффурами и являетесь чайником, пожалуйста, начните с урока Дифференциальные уравнения первого порядка. Примеры решений. Согласитесь, плохо быть в неважной форме.
Во-вторых, необходимо уверенно находить частные производные. Всё будет крутиться вокруг них. Счастливые студенты, которые избежали плотного знакомства с частными производными на первом курсе, будут вынуждены добавить их в свои друзья, поскольку без навыков нахождения частных производных читать дальше просто нет смысла.
С любимых незабываемых частных производных и начнём.
Рассмотрим функцию двух переменных:

Такая вот простенькая функция.
Требуется найти частные производные первого порядка  ,
,  и составить полный дифференциал
и составить полный дифференциал  .
.
В контексте данного урока я поменяю букву «зет» на букву «эф»:
Дана функция двух переменных  . Требуется найти частные производные первого порядка
. Требуется найти частные производные первого порядка  ,
,  и составить полный дифференциал
и составить полный дифференциал 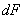 .
.
Зачем потребовалась смена буквы? Традиционно сложилось, что в рассматриваемой теме в ходу буква  . Кроме того, частные производные первого порядка будем чаще обозначать значками
. Кроме того, частные производные первого порядка будем чаще обозначать значками  . Как мы помним из вводного урока про дифференциальные уравнения первого порядка, в диффурах «не в почёте» обозначать производную штрихом.
. Как мы помним из вводного урока про дифференциальные уравнения первого порядка, в диффурах «не в почёте» обозначать производную штрихом.
Решаем нашу короткую задачку.
Найдем частные производные первого порядка:

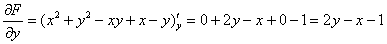
Полный дифференциал составим по формуле:
 , или, то же самое:
, или, то же самое: 
В данном случае: 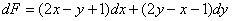
Пример 1
Решить дифференциальное уравнение 
Не ожидали? =)
Но самое забавное, что уже известен ответ:  , точнее, надо еще добавить константу:
, точнее, надо еще добавить константу:
Общий интеграл  является решением дифференциального уравнения
является решением дифференциального уравнения  .
.
Таким образом, дифференциальное уравнение  является полным дифференциалом функции
является полным дифференциалом функции  . Отсюда и название разновидности ДУ – уравнения в полных дифференциалах.
. Отсюда и название разновидности ДУ – уравнения в полных дифференциалах.
Как решить диффур в полных дифференциалах? Очевидно, что нужно выполнить некоторые обратные действия, чтобы восстановить исходную функцию (общий интеграл). Не так давно я что-то там дифференцировал. Какое действие является обратным? Правильно, интегрирование. То есть, речь пойдет о частном интегрировании, которое часто используется и в других задачах, упомянутых в начале урока.
|
из
5.00
|
Обсуждение в статье: Как решить линейное уравнение? |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

