 |
Главная |
Вывод: Уравнение Бернулли с помощью замены сводится к линейному неоднородному уравнению первого порядка
|
из
5.00
|
Я сменю у каждого слагаемого знак, делать это не обязательно, просто запись будет выглядеть стандартнее что ли:

Дальше алгоритм работает по накатанной колее, важно только уметь решать неоднородное уравнение 1-го порядка:
Проведем замену: 
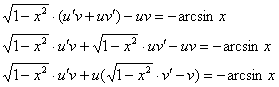
Составим и решим систему:

Из первого уравнения найдем  :
:

 – подставим найденную функцию во второе уравнение системы:
– подставим найденную функцию во второе уравнение системы:

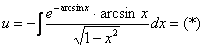
Подобные интегралы я ласково называю дурными интегралами, они не столько сложные, сколько творческие – нужно догадаться (хотя бы научным тыком), как их решать.
Данный интеграл берётся по частям:


Творчество присутствует, помимо интегрирования по частям, использован метод подведения функции под знак дифференциала.
Таким образом:

Но это ещё не всё, выполняем обратную замену:
Если изначально было  , то обратно будет
, то обратно будет 
В результате получаем общее решение исходного уравнения Бернулли:

Тривиальное решение 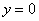 потерялось (это произошло в самом начале при делении на
потерялось (это произошло в самом начале при делении на  ) и не вошло в общий интеграл. Однако это обстоятельство нас совершенно не волнует, поскольку по условию требовалось решить только задачу Коши (! заметьте, что если бы условие требовало указать в ответе и общее решение, то его следовало бы дополнить функцией
) и не вошло в общий интеграл. Однако это обстоятельство нас совершенно не волнует, поскольку по условию требовалось решить только задачу Коши (! заметьте, что если бы условие требовало указать в ответе и общее решение, то его следовало бы дополнить функцией 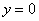 ). Найдем частное решение, удовлетворяющее начальному условию
). Найдем частное решение, удовлетворяющее начальному условию  :
:

Ответ: частное решение: 
Для мастодонтов дифференциального исчисления вкратце напоминаю алгоритм проверки дифференциального уравнения:
1) проверяем, выполнено ли начальное условие;
2) берём ответ  и находим производную
и находим производную 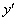 ;
;
3) подставляем ответ  и найденную производную
и найденную производную 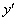 в исходное ДУ – должно получиться верное равенство.
в исходное ДУ – должно получиться верное равенство.
Проверить дифференциальное уравнение Бернулли действительно не всем под силу, так как в большинстве случаев приходится находить трудную производную и выполнять громоздкую подстановку.
Когда я подбирал первый пример для этой статьи, то очень хотелось разобрать распространенное уравнение Бернулли в духе  , однако сразу же после замены оно становится до неприличия похоже на Пример 8 урока неоднородные дифференциальные уравнения первого порядка. Поэтому пусть лучше будет что-нибудь необычное.
, однако сразу же после замены оно становится до неприличия похоже на Пример 8 урока неоднородные дифференциальные уравнения первого порядка. Поэтому пусть лучше будет что-нибудь необычное.
Но, вы не расстраивайтесь, вот пара более простых примеров для самостоятельного решения:
Пример 2
Найти решение ДУ  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 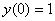
Пример 3
Найти решение задачи Коши
 ,
, 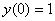
Полные решения и ответы в конце урока.
В третьем примере перед решением целесообразно представить уравнение в стандартном виде: 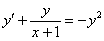 .
.
Вообще, иногда составители сборников и методичек зашифровывают уравнения до неузнаваемости, например:

Как говорится, сиди студент и разгадывай ребус – какого хрена типа этот диффур. То ли уравнение с разделяющимися переменными, то ли уравнение в полных дифференциалах, то ли еще какое-нибудь уравнение.
Интереснейшая задача и новая информация, о которой я до сих пор не рассказывал:
Пример 4
Найти решение ДУ  , соответствующее начальному условию
, соответствующее начальному условию 
Корни, куда же без них.
Решение: Пожалуйста, классический вид 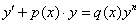 уравнения Бернулли.
уравнения Бернулли.
По условию требуется решить только задачу Коши, поэтому ось абсцисс 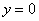 снова идёт лесом.
снова идёт лесом.
Сначала убираем «игрек» из правой части, для этого делим каждую часть на  :
:

Теперь с помощью замены нужно избавиться от «игрека» вот в этом слагаемом:

Из вышесказанного следует замена: 
Найдем производную:
 , откуда выразим:
, откуда выразим: 
Таким образом:


Получено линейное неоднородное уравнение, проведем замену: 


Составим и решим систему:  .
.
Из первого уравнения найдем  :
:
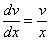


 – подставим во второе уравнение:
– подставим во второе уравнение:



Таким образом: 
Обратная замена: если  , то
, то 
Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:

…вот тебе и раз. Уравнение  имеет два корня
имеет два корня  и в результате получаются… два частных решения
и в результате получаются… два частных решения  , каждое из которых удовлетворяет начальному условию
, каждое из которых удовлетворяет начальному условию  . Желающие могут выполнить проверку для обеих функций. Однако зададимся вопросом, а могло ли такое получиться в принципе? Может быть где-нибудь допущена ошибка?
. Желающие могут выполнить проверку для обеих функций. Однако зададимся вопросом, а могло ли такое получиться в принципе? Может быть где-нибудь допущена ошибка?
Скорее всего, у многих читателей ещё с 1-го урока сложился стереотип, что частное решение всегда единственно. Это далеко не так. В теории математического анализа строго доказано, что задача Коши имеет единственное решение лишь при выполнении определённых условий (соответствующая теорема формулируется в первых параграфах любого учебника/раздела, посвященного диффурам).
В данном случае условие единственности нарушено, и в точке  пересекаются (именно пересекаются, а не касаются друг друга!) графики многочленов
пересекаются (именно пересекаются, а не касаются друг друга!) графики многочленов  .
.
Ответ:начальному условию  соотвествуют два частных решения:
соотвествуют два частных решения: 
А сейчас небольшой оффтопик. Надеюсь, вы хорошо изучили раздел «Функции и графики» и представляете, как выглядит типичный график многочлена 4-ой степени. Семейство кривых  (общее решение ДУ) располагается в верхней полуплоскости и касается оси абсцисс в каждой её точке. Образно говоря, множество графиков
(общее решение ДУ) располагается в верхней полуплоскости и касается оси абсцисс в каждой её точке. Образно говоря, множество графиков  (при всех действительных значениях константы) своими точками касания порождает решение
(при всех действительных значениях константы) своими точками касания порождает решение 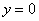 , которое, как заправский партизан засело в чаще леса и в общее решение не вошло.
, которое, как заправский партизан засело в чаще леса и в общее решение не вошло.
Такое необычное решение называют особым решениемдифференциального уравнения.
В общем случае особое решение тоже представляет собой кривую, которая огибает «основное семейство». В рассмотренном же примере оно больше ассоциируется с «подставкой» под графики функций  .
.
Потёрто.
Возможно, некоторые удивились, почему я ничего не рассказал про математика Бернулли. Забыл. Не будем нарушать традиций. Якоб Бернулли почти итальянец, жил в Швейцарии, говорил на 5-ти языках. В семье Бернулли 9 (!) математиков, причём у некоторых представителей династии есть серьёзные достижения и в области физики. …Пожалуй, этой информации будет достаточно, а то мне в голову стал приходить крайне неэтичный юмор в духе «Якоб, Иоганн – какая студенту разница?» =) …Побродил немного по комнате, посмеялся, продолжаю:
Пример 5
Найти общее решение (или общий интеграл) дифференциального уравнения первого порядка.
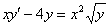
Немногочисленный пример из моей выборки, когда требуется найти только общее решение. Полное решение и ответ в конце урока.
Мы рассмотрели наиболее распространенные версии уравнения Бернулли – с «игреком» во второй степени и с «игреком» под квадратным корнем. Другие варианты встречаются реже. Разберём пример, когда «игрек» находится в кубе.
Пример 6
Найти общее решение дифференциального уравнения

Решение: Данное ДУ является уравнением Бернулли.
Очевидно, что 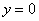 является решением этого уравнение.
является решением этого уравнение.
И только после этой оговорки делим обе части на  :
:

Избавляемся от «игрека» в «полюбившемся» слагаемом, для этого проведем замену:

В результате:


Получено линейное уравнение, проведем замену: 


Решим систему:

Из первого уравнения найдем  :
:




 – подставим во второе уравнение:
– подставим во второе уравнение:
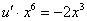


Таким образом: 
Проведём обратную замену: если изначально  , то обратно:
, то обратно: 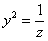

В принципе, здесь можно выразить общее решение в виде:
 , но, согласитесь, смотрится не очень…, словно Дедушка Мороз подсунул в подарок гнилую мандаринку. Эта фишка уже рассматривалась мной на уроке Однородные дифференциальные уравнения первого порядка. Нет-нет, испорченные продукты питания никому не предлагал =)
, но, согласитесь, смотрится не очень…, словно Дедушка Мороз подсунул в подарок гнилую мандаринку. Эта фишка уже рассматривалась мной на уроке Однородные дифференциальные уравнения первого порядка. Нет-нет, испорченные продукты питания никому не предлагал =)
Лично я в похожей ситуации почти всегда склоняюсь к тому, чтобы оставить ответ в виде общего интеграла (заодно париться не нужно).
Ответ: общий интеграл:  . Ещё одно решение:
. Ещё одно решение: 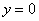
Перед кремлёвским салютом рассмотрим заключительный пример с отрицательной степенью.
Пример 7
Найти частное решение дифференциального уравнения
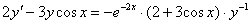 ,
, 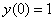
Это пример для самостоятельного решения.
Ну вот, мешок с подарками пуст, надеюсь все остались довольны. Хотя, честно, Новый Год не люблю, сегодня вычитал на Анекдоте.ру меткий афоризм: 10 дней праздников обычно проводишь либо без всякой пользы либо с большим вредом.
Удачной вам сессии!
Решения и ответы:
Пример 2: Решение: Данное ДУ является уравнением Бернулли. Найдем общее решение.


Проведем замену: 

Получено линейное неоднородное уравнение, замена:  .
.


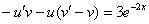
Составим и решим систему: 
Из первого уравнения найдем  :
:



 – подставим во второе уравнение:
– подставим во второе уравнение:



Таким образом: 
Обратная замена: 
Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:
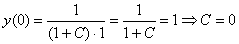
Ответ: частное решение: 
Красиво.
Пример 3: Решение: 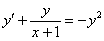
Данное дифференциальное уравнение является уравнением Бернулли, разделим обе части на  :
:

Проведем замену: 


Получено линейное неоднородное уравнение, проведем замену:



Составим и решим систему:

Из первого уравнения найдем  :
:



 – подставим во второе уравнение:
– подставим во второе уравнение:



Таким образом:

Обратная замена: 
Общее решение: 
Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение: 
Пример 5: Решение: Данное уравнение является уравнением Бернулли.
Очевидно, что 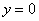 является решением данного уравнения.
является решением данного уравнения.


Замена: 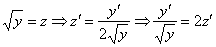

В полученном линейном неоднородном уравнении, проведем замену: 



Решим систему:  .
.
Из первого уравнения найдем  :
:




 – подставим во второе уравнение:
– подставим во второе уравнение:



Таким образом:
Общее решение: 
Обратная замена:
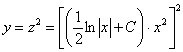
Ответ: общее решение 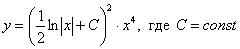 ; ещё одно решение:
; ещё одно решение: 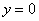
Пример 7: Решение: 
Данное ДУ является уравнением Бернулли.

Проведем замену: 

Получено линейное неоднородное уравнение, проведем замену:



Составим и решим систему:

Из первого уравнения найдем  :
:



 – подставим во второе уравнение:
– подставим во второе уравнение:



Таким образом:

Обратная замена: 
Частное решение, соответствующее начальному условию 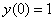 , можно найти прямо из общего интеграла
, можно найти прямо из общего интеграла  . Для этого вместо «икса» подставляем ноль, а вместо «игрека» – единицу:
. Для этого вместо «икса» подставляем ноль, а вместо «игрека» – единицу:

Таким образом, частное решение:

Частное решение также выясняется и более «привычным» способом через общее решение  .
.
Ответ: частное решение: 
|
из
5.00
|
Обсуждение в статье: Вывод: Уравнение Бернулли с помощью замены сводится к линейному неоднородному уравнению первого порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

