Схема с повторением испытаний (схема Бернулли)

Рассмотрим следующую часто встречающуюся ситуацию.

1. Проводится серия n независимых испытаний. незави­симость испытаний означает, что при выполнении каждого следующего испытания полностью восстанавливается ком­плекс условий, при которых выполнялось предыдущее испытание.

2. При каждом испытании интересующее нас событие А (успех) наступает с вероятностью р и не наступает с вероятностью q = 1 – p. такую ситуацию будем называть схемой с повторением испытаний или схемой бернулли.

Обозначим через x число успехов в серии из n независимых испытаний. Очевидно, x в зависимости от случая принимает значения

0, 1, 2, …, n.

Каковы вероятности этих значений?

Теорема 1.Справедлива формула

, k = 0, 1,…, n. (11)

эта формула называется формулой Бернулли.

Доказательство.

.

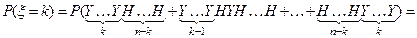
Здесь Y (успех) – появление события А, Н (неуспех)– непоявление события А.

Число слагаемых в этой сумме равно числу способов выбрать k мест из n свободных мест, то есть числу сочетаний из n по k:

,

что и требовалось доказать.

Пример 1. Проводится десять независимых бросаний монеты. Найти вероятность того, что три раза из 10 выпадет герб.

Решение. Здесь успех – выпадение герба, x – число успехов, p = q = , n = 10, k =3. Следовательно, из формулы (11) имеем

.

Пример 2. Проводится 100 независимых бросаний монеты. Найти Р (40≤ x≤ 60), x - число выпадений герба.

Решение.

Р (40≤ x≤ 60) = Р(x = 40) + Р(x = 41) + Р(x = 42) + … +

+ Р(x = 60) = .

Мы видим: если в схеме Бернулли число испытаний n велико, то подсчет вероятностей вида P(m₁ ≤ x≤ m₂) с помощью формулы Бернулли весьма затруд­нен.

укажем приближенную формулу для подсчета таких ве­роятностей, доказанную независимо французскими математи­ками Муавром и Лапласом.

для этого вначале введем функцию, которая называется функцией Лапласа и обозначается Ф(х):

. (12)

Укажем график и некоторые свойства этой функции.

1⁰. Ф(0) = 0;

2⁰. Ф (– х) = – Ф(х);

3⁰. если | x | ≥ 3, то Ф (х) » ± 0,5 с большой точностью.

Для функции Лапласа имеются таблицы.

Теорема 2. В схеме Бернулли при достаточно большом числе испытаний справедлива приближенная формула:

P(m₁ ≤ x ≤ m₂) » . (13)

эта формула называется интегральной формулой Муавра-Лапласа. Доказательство этой формулы приводится в §3 главы 3. Вычисления показывают, что эта формула является практически точной при n ≥ 30.

Вернемся к решению примера 2.

решение. Здесь n =100, p = q = . По формуле Муавра-Лапласа найдем

Р (40 ≤ x ≤ 60)

Замечание. Интегральная формула Муавра-лапласа указывает правила вычисления вероятности неравенств вида P(m₁ ≤ x ≤ m₂) в схеме Бернулли при большом числе испытаний. Укажем правило вычисления вероятностей P(x=k) в этой ситуации.

Рассмотрим функцию

.

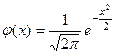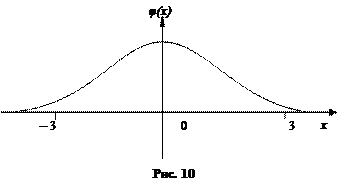Очевидно, φ(х) связана с функцией Лапласа равенством

.

При большом числе испытаний справедлива приближенная формула

. ( )

эта формула называется локальной формулой Муавра-Лапласа. Для функции (13^') имеются таблицы.

Глава 2. Случайные величины