Дисперсия дискретной случайной величины

Пусть

;

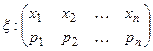m_x = x₁· p₁ + x₂ · p₂ + … + x_n · p_n – математическое ожидание x (центр);

x – m_x – отклонение x от центра;

(x – m_x)² – квадрат отклонения x от центра.

Очевидно,

(x – m_x)² : .

Дисперсией дискретной случайной величины x называется матема­тическое ожидание квадрата отклонений от центра:

D[ x ] = D_x = M[(x – m_x)²] = p₁ (x₁– m_x)² + p₂ (x₂– m_x)² +…+ + p_n(x_n – m_x)².

 

пример 1. 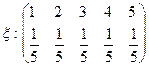, m_x = 3,

Пример 2.

, m_x = 3, D_x = 1.

 

Помнить: дисперсия характеризует разброс случайной величины относительно центра с учетом возможных значений и их вероятностей.

 

Свойства дисперсии:

1⁰. D [ a ] = 0;

2⁰. D [ a x ] = a² D_x;

3⁰. если x, h статистически независимы, то

D [ x + h ] = D [ x ] + D [ h ].

4⁰. D_x = M [x ² ] – .

доказательство.

Первое и второе свойства непосредственно вытекают из определения и соответствующего свойства математического ожидания (доказать самостоятельно).

3⁰. D [ x + h] = M [(x + h – m_{x + h})²] = m [(x + h – m_x – – m_h)²] = M [(x – m_x+ h – m_h)²] = M [(x– m_x)² + (h – m_h)² + + 2(x– m_x)(h – m_h)] = M [(x– m_x)² ] + M [(h – m_h)²] + 2 M [x – – m_x ]·M[h – m_h] = D_x +d_h +2(m_x – m_x)(m_h – m_x) = D_x +d_h, что и требовалось.

 

Здесь существенно использовалась статистическая независимость случайных величин x – m_x, h – m_h.

4⁰. D_x = M [(x– m_x)² ] = M [x ² – 2x m_x + ] = M [x ²] –

– 2 M [x ]· m_x + = M [x ²] – .

 

Величина

называется среднеквадратическим отклонением (СКО) случайной величины x . Очевидно, s_x имеет тот же смысл, что и D_x – характеризует разброс случайной величины относительно центра с учетом возможных значений и их вероятностей. СКО имеет ту же физическую размерность, что и случайная величина x.

Закон распределения и числовые характеристики непрерывной случайной величины

Мы знаем, что закон распределения дискретной случайной величины x задается таблицей, в которой перечислены ее возможные значения и указаны их вероятности. Для непрерывных случайных величин задание закона распределения в виде такой таблицы невозможно, так как в этом случае вероятности отдельных значений равны нулю.

 

Пример.

Испытание: берут наугад точку x на чи­словой оси так, что значения на от­резке [0, 1] равновозможны, остальные значе­ния невозможны. Очевидно, x – непре­рывная случайная величина.

Найдем

.

 

Закон распределения непрерывной случайной вели­чины может быть задан двумя способами:

1. с помощью функции распределения F (x);

2. с помощью плотности вероятности f (x).

 

Функция распределения

 

Пусть с испытанием связана непрерывная случайная величина x.

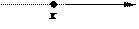Зафиксируем произвольное число х. В зависимости от случая возможны три исхода испытания:

x > x, x = x, x < x.

Каждое из этих трех событий случайно, поэтому имеет смысл говорить об их вероятности. Обозначим

F (x) = p (x < x).

Функция F(x) называется функцией распределения случайной величины x.

 

 

 

Рис. 11

свойства функции распределения

1⁰. 0 ≤ F (x) ≤ 1;

2⁰. F (x) монотонно не убывает (рис. 11);

3⁰. F (– ¥) = 0, F (+ ¥) = 1;

4⁰. P (a<x< b) = F (b) – F (a).

доказательство.

1. Это свойство вытекает из того, что вероятность любого события есть число, принадлежащее [0, 1].

2. Это свойство вытекает из того, что при увеличении х интервал ( – ¥, х) расширяется, поэтому вероятность попадания в этот интервал не уменьшается.

3. F (– ¥) ,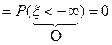

F (+ ¥) .

4. Имеем:

F (b) = P (x < b) = =

= P (x < a) + P (x = a) + P (x Î (a, b)) = F (a) + 0 + P (a<x< b).

 

Отсюда вытекает требуемое равенство 4⁰.

Замечание. Функция распределения F (x) имеет смысл и для дискретных случайных величин. Например, функция распределения случайной величины

x :

представляет собой кусочно-постоянную функцию, график которой изображен на рис. 12 (кружок означает, что в этом месте отсутствует точка на графике).

 

 

Рис. 12

Проверим это для случаев х >3, 2≤ х< 3. В первом случае имеем

F (x) = P (x < x) = P (x = 1 или x = 2 или x = 3) =

= P (x = 1) + P (x = 2) + P (x = 3) = 0,25 + 0,25 + 0,5 = 1.

Во втором случае

F (x) = P (x = 1 или x = 2) = Р (x = 1) + Р (x = 2) =

= 0,25 + 0,25 = 0,5.

Оставшиеся случаи 1≤ х< 2, x<1 предлагаем рассмотреть са­мостоятельно.

 

Плотность вероятности

 

[ ] Пусть с испытанием связана непрерыв­ная случайная величина x.

Плотностью вероятности случайной величины x в точке х называется предел отношения вероятности попадания в отрезок [x, x + Dx] к длине отрезка Dx при условии, что отрезок стягивается к точке х:

.

Нестрого говоря, плотность вероятности – это вероятность попадания в отрезок длины 1.

 

Свойства плотности вероятности:

1⁰. f (x) ≥ 0 при всех х.

2⁰. P (x Î (a,b)) =

вероятность попадания в интервал равна заштрихованной площади (рис. 13).

 

Рис. 13

 

3⁰. Площадь S бесконечной фигуры, ограниченной графи­ком плотности f (x) и осью абсцисс, равна 1 (рис. 13): S = 1.

 

Доказательство.

1. Это свойство вытекает из того, что предел неотрица­тельной функции неотрицателен.

2. Имеем

.

Отсюда получаем

;

учтено свойство 4⁰ функции распределения.

3. .

Помнить: кривая плотности вероятности показывает, как суммарная вероятность 100% распределяется по интервалам.

Замечание. Рассмотрим два крайних случая (рис.14, 15). В первом случае с вероятностью, близкой к единице, случайная величина x принимает значения, близкие к х₀, в этом случае можно без большой погрешности считать, что x- неслучайная величина: x » х₀. Во втором случае суммарная вероятность 100% приблизительно равномерно распреде-лена по широкому спектру возможных значений, то есть в этом случае x сильно случайная величина.

 

 

 

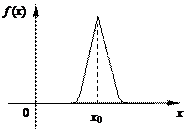Рис. 14 Рис. 15

 

Связь между f (x) и F(x)

 

Пусть с испытанием связана непрерывная случайная величина x с плотностью вероятности f (x) и функцией распределения F (x). Справедливы равенства

1⁰. ;

2⁰. .

доказательство.

1. по свойству плотно­сти вероятности.

2. Это свойство было доказано выше (см. доказатель­ство свойства 2⁰ плотности).

 

Пример. Берут наугад точку x на оси так, что значения на [0, 1] равновозможны, а остальные невозможны. Найти: а) функцию распределения F(x); б) плотность вероятности f(x).

Решение.а) F(x) – ? [ ]

Пусть

1. х ≤ 0: F (x) = P (x < x) = 0.

2. 0 < x≤ 1: F (x) = P (x < x) = P ( – ¥ < x≤ 0 или 0 < x < x) =

= P( – ¥ < x ≤ 0) + P (0 < x < x) = 0 + 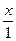= x.

3. x > 1: F (x) = P (x < x) = P (x≤ 0 или 0 < x ≤ 1 или 1 <x < x) =

45 46

= P (x ≤ 0) + P (0 < x ≤ 1) + P( 1 < x < x) = 0 + 1 + 0 = 1.

Окончательно имеем

 

 

б) f (x) – ? , отсюда

Замечание. Если график плотности вероятности имеет вид, изображенный на рис. 16, то говорят, что случайная величина x равномерно распределена на [a, b].

 

График функции распределения для такой случайной величины имеет вид, изображенный на рис. 17.

 

 

Числовые характеристики

 

Напомним, что для дискретной случайной величины числовые характеристики определяются формулами:

m_x = x₁p₁ + x₂p₂ + … x_np_n = ;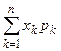

D_x = M [(x – m_x)²] = ;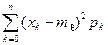

.

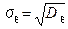Числовые характеристики непрерывной случайной величины определяются формулами

; ; .

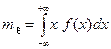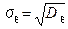Эти величины имеют такой же смысл, как в дискретном случае: математическое ожидание характеризует центральное значение случайной величины, дисперсия и СКО – разброс относительно центра. Сохраняют, как можно доказать, все свойства математического ожидания и дисперсии, доказанные в дискретном случае.

47 48

Пример. Найти числовые характеристики для равномерно распределенной на [a, b] случайной величины x.

Решение. Имеем из замечания (рис.16)

Тогда

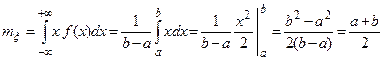
Следовательно,

, , . (14)