 |
Главная |
Частные производные. Дифференциальные функции
|
из
5.00
|
 Рис.10.6
Рис.10.6
Пусть функция  определена в точке М0 (x, y)
определена в точке М0 (x, y)  D и некоторой её окрестности. Её графиком является поверхность
D и некоторой её окрестности. Её графиком является поверхность  . Точке М0 (x, y) соответствует на поверхности точка P0(x0,y0,z0) (Рис. 10.6). Дадим аргументам x и y приращения
. Точке М0 (x, y) соответствует на поверхности точка P0(x0,y0,z0) (Рис. 10.6). Дадим аргументам x и y приращения  и
и  соответственно. Тогда функция Z получит полное приращение
соответственно. Тогда функция Z получит полное приращение
 , где точка
, где точка
 . Если дать приращение только аргументу x, зафиксировав значение аргумента y , то функция z получит частное приращение
. Если дать приращение только аргументу x, зафиксировав значение аргумента y , то функция z получит частное приращение  , измеряемое величиной отрезка
, измеряемое величиной отрезка  (Рис.10.6). Аналогично вводится понятие частного приращения
(Рис.10.6). Аналогично вводится понятие частного приращения  равного величине
равного величине  .
.
 Определение. Предел отношения соответствующего частного приращения функции к приращению рассматриваемого аргумента, когда последнее стремится к нулю, вычисленный в предположении того, что второй аргумент сохраняет постоянное значение (если этот предел существует), называется частной производной функции двух переменных по соответствующей переменной.
Определение. Предел отношения соответствующего частного приращения функции к приращению рассматриваемого аргумента, когда последнее стремится к нулю, вычисленный в предположении того, что второй аргумент сохраняет постоянное значение (если этот предел существует), называется частной производной функции двух переменных по соответствующей переменной.
Обозначаются частные производные следующим образом:


Аналогично вводится понятие частных производных для функции трех и более переменных.
Геометрический смысл частных производных функций показан на рис. 10.6. Частная производная  , где
, где  - угол наклона касательной к поверхности
- угол наклона касательной к поверхности  и осью ОX в сечении этой поверхности плоскостью x=x0.
и осью ОX в сечении этой поверхности плоскостью x=x0.
Пример.Найти частные производные функций
1. z = x2 + y2 - 3xy + x3y
Расматривая y как константу, а затем x как константу, получаем соответственно 
 .
.
2. 

Обобщая понятие дифференциала функции одной переменной на случай функции двух переменных, введем определения.
 Определение. Выражение
Определение. Выражение  называется полным дифференциалом функции двух переменных.
называется полным дифференциалом функции двух переменных.
Как и для функции одной переменной для независимых переменных 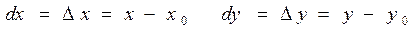 Следовательно, полный дифференциал в точке Мо (x0 , y0):
Следовательно, полный дифференциал в точке Мо (x0 , y0):

представляет собой линейное выражение. По аналогии с функцией одной переменной можно показать, что полное приращение функции f(x,y)
 (10.3).
(10.3).

 и
и  - бесконечно малые величины. В этом случае дифференциал
- бесконечно малые величины. В этом случае дифференциал  есть главная линейная часть приращения функции z = f(x,y).
есть главная линейная часть приращения функции z = f(x,y).
Определение. Если полное приращение функции z = f(x,y) может быть представлено в виде (10.3), функция f(x,y) называется дифференцируемойв точке (x,y).
Пусть функция z = f(x,y) непрерывна в точке (x,y) и имеет в ней частные производные  и
и  . Эти производные, в свою очередь, являются функциями двух переменных, и если они непрерывны, то можно ставить вопрос о существовании для них производных по любому из аргументов. Эти производные называются частными производными второго порядка функции z.
. Эти производные, в свою очередь, являются функциями двух переменных, и если они непрерывны, то можно ставить вопрос о существовании для них производных по любому из аргументов. Эти производные называются частными производными второго порядка функции z.
 ;
;
 ;
;
 ;
;

 и
и  называются смешанными частными производными второго порядка. Имеет место следующая теорема.
называются смешанными частными производными второго порядка. Имеет место следующая теорема.
Если смешанные частные производные второго порядка функции
z = f(x,y) непрерывны в некоторой точке М0 (x0, y0), то они в ней равны  =
= 
Пример. Найти частные производные второго порядка функции  . Находим частные производные первого порядка.
. Находим частные производные первого порядка.






Убеждаемся, что 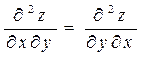
|
из
5.00
|
Обсуждение в статье: Частные производные. Дифференциальные функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

