 |
Главная |
Первообразная и неопределенный интеграл
|
из
5.00
|
При решении многих задач физики, математики требуется по заданной функции  найти ее производную
найти ее производную 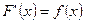 Но достаточно часто приходится сталкивать с обратными задачами, когда по известной производной
Но достаточно часто приходится сталкивать с обратными задачами, когда по известной производной  требуется найти саму функцию
требуется найти саму функцию  .
.
 Например, по закону измерения скорости V=V(t) необходимо найти закон движения S=S(t). Но
Например, по закону измерения скорости V=V(t) необходимо найти закон движения S=S(t). Но  . Таким образом, по известной производной
. Таким образом, по известной производной  следует найти функцию
следует найти функцию  .
.
 Определение. Операция отыскания функции по ее производной называется интегрированием, а раздел математики, изучающий способы интегрирования функций – интегральным исчислением.
Определение. Операция отыскания функции по ее производной называется интегрированием, а раздел математики, изучающий способы интегрирования функций – интегральным исчислением.
Определение. Функция  , определенная на промежутке
, определенная на промежутке  называется первообразной для функции
называется первообразной для функции  на том же отрезке, если для любого
на том же отрезке, если для любого  имеет место равенство
имеет место равенство 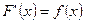
Примеры.

Очевидно, что если  - первообразная для функции
- первообразная для функции  , то
, то  , где
, где  есть также первообразная той же функции.
есть также первообразная той же функции.
Действительно, пусть 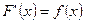 , но и
, но и  .
.
Вывод: если функция  имеет хотя бы одну первообразную, то для нее существует бесчисленное множество первообразных.
имеет хотя бы одну первообразную, то для нее существует бесчисленное множество первообразных.
Теорема 11.1.
Если  некоторая первообразная функции
некоторая первообразная функции  , то выражение
, то выражение  ,
,
где С – произвольная постоянная величина, исчерпывает множество всех
первообразных функции  на данном промежутке.
на данном промежутке.
Доказательство.
Пусть  наряду с
наряду с  есть первообразная функции
есть первообразная функции  . Это означает, что:
. Это означает, что:

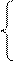
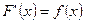
отсюда  , то есть
, то есть  ,
,
или 
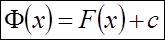 .
.
иными словами, любые первообразные функции  отмечаются на постоянную величину.
отмечаются на постоянную величину.
 Функция
Функция  имеющая на некотором промежутке первообразную, называется интегрируемой на этом промежутке.
имеющая на некотором промежутке первообразную, называется интегрируемой на этом промежутке.
Определение. Множество всех первообразных для функции  на данном промежутке называется неопределенным интегралом и обозначается следующим образом
на данном промежутке называется неопределенным интегралом и обозначается следующим образом

 – подынтегральная функция
– подынтегральная функция
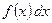 – подынтегральное выражение
– подынтегральное выражение
 Очевидно, операция интегрирования ставит соответствие функции
Очевидно, операция интегрирования ставит соответствие функции  бесчисленное множество функций (первообразных)
бесчисленное множество функций (первообразных)  или говорят семейство функций.
или говорят семейство функций.
|
 означает нахождение уравнения кривой по известному в каждой ее точке угловому коэффициенту касательной. Очевидно, в силу произвольности С таких кривых существует бесчисленное множество. Геометрически это объясняется тем, что в каждой задается лишь направление касательной, а не сама касательная. Каждая кривая
означает нахождение уравнения кривой по известному в каждой ее точке угловому коэффициенту касательной. Очевидно, в силу произвольности С таких кривых существует бесчисленное множество. Геометрически это объясняется тем, что в каждой задается лишь направление касательной, а не сама касательная. Каждая кривая  получается с параллельным любой из них вверх (вниз). Каждая из кривых называется интегральной кривой.
получается с параллельным любой из них вверх (вниз). Каждая из кривых называется интегральной кривой.
Таким образом, с геометрической точки зрения неопределенный интеграл представляет собой бесчисленное множество (или семейство) интегральных кривых.
Пример  – семейство кубических парабол.
– семейство кубических парабол.
Теорема существования неопределенного интеграла.Если
подынтегральная функция  непрерывна на некотором отрезке, то она на
непрерывна на некотором отрезке, то она на
нем интегрируема.
|
из
5.00
|
Обсуждение в статье: Первообразная и неопределенный интеграл |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

