Измерение тесноты связи признаков шкалы наименований

 

А) Связь 2-х альтернативных признаков (измеримых по шкале дихотомии)

X:{0,1}

Y:{0,1}

 

В этом случае строится таблица сопряженности 2х2:

 

Y \ X			S
	a	b	a+b
	c	d	c+d
S	a+c	b+d	N

 

Здесь, например, параметр b - число элементов выборки, имеющих значение 0 признака Y и 1 - признака X.

 

Для анализа тесноты связи в данном случае можно использовать коэффициент ассоциации Пирсона:

 

 

 

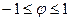
Или коэффициент контингенции Юла:

 

 

Пример: Оценить связь между предпочтением при голосовании на выборах избирателей (Y) и фактом наличия у избирателей работы (X).

 

 

Обследованию подверглись 200 человек.

 

 

Y X			S
S

 

Требуется вычислить j и K_k

 

 

Б) Признаки, измеренные по шкале наименований с числом значений больше двух.

 

X Y			…	nx	S
			…
			…
…	…	…	…	…	…
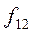
ny			…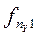
			…

 

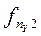
n_x – число возможных значений признака X.

n_y– число возможных значений признака Y.

 

Используется коэффициент взаимной сопряженности Чупрова:

 

 

Используется также коэффициент сопряженности Пирсона:

 

 

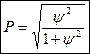
Здесь в знаменателе 1-го слагаемого стоит произведение сумм элементов строки i и столбца j, на пересечении которых стоит частота f_ij.

 

Случай дихотомической величины X и порядковой Y.

Коэффициент бисериальной ранговой корреляции:

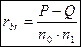
n_o-количество объектов имеющих x=0, n₁ ® x=1.

x	y		ry(x=1)	ry(x=0)	Pi	Qi

В столбец P_i напротив каждого ранга из 1-го столбца записывается количество рангов из 2-го столбца стоящих ниже этого ранга из 1-го столбца.

В столбце Q_i напротив каждого ранга из 2-го столбца записывается количество рангов из 1-го столбца, стоящих ниже этого ранга из 2-го столбца.

 

Случай дихотомической величины Х и количественной Y

Коэффициент бисериальной корреляции

Пример: Связь между величиной зарплаты Y (руб.) и величиной X (доволен з/п(1) или нет(0)).

n₀ – количество объектов имеющих x=0

n₁ – количество объектов имеющих x=1

n₀+n₁=n

- среднее квадратичное отклонение по всем Y

- среднее значение для Y, у которых X=1

- среднее значение для Y, у которых X=0

 

Оценка существенности уравнения регрессии

Производится на основе F-критерия Фишера

pac - расчетный

m – число параметров в уравнении регрессии

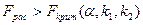
k₁=m-1, k₂=n-m

 

Оценка существенности коэффициента корреляции

При большом объеме выборки используется соотношение для коэффициента корреляции и его среднеквадратичной ошибки

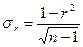
Если то следует говорить о существенности коэффициента корреляции.

При недостаточно большом объеме выборки величина ошибки .

При этом .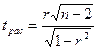

 

Формула Спирмена для корреляции связанных рангов

j – номера связок по порядку для признака X,

A_j – число одинаковых рангов j-ой связки по X,

k – номера связок по Y,

B_k – число одинаковых рангов по Y в k-ой связке.

 

Множественная корреляция