 |
Главная |
Преобразование не ключевых строк
|
из
5.00
|
Для преобразования не ключевой строки нужно каждый элемент преобразованной ключевой строки умножить на дополнительный множитель преобразуемой строки и добавить к соответствующему элементу.
5. Если в ходе вычислений появляется строка вида:
| b | x1 | x2 | …… | xn |
| b≠0 | ……. |
т.е. строка, в которой все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, то система не имеет решений.
Действительно, всякое решение системы должно удовлетворять уравнению, записанному в этой строке, которое имеет вид:
 ...................................................
...................................................
Поскольку его левая часть равна нулю для любых значений x1, x2,…, xn, а правая часть отлична от нуля, то ему не может удовлетворять ни один такой набор.
6. Если в ходе вычислений появляется строка, состоящая из одних нулей, то ее можно удалить из таблицы, так как такая строка отвечает уравнению:
 |
которому удовлетворяет любой набор значений x1, x2,…, xn и поэтому ее можно не учитывать.
Заметим, что появление строки из одних нулей свидетельствует о том, что записанное в ней уравнение является следствием других уравнений системы.
Если при применении алгоритма не возникает противоречивой ситуации, описанной в п.5, то в каждой строке заключительной таблицы (т.е. в каждом уравнении) имеется базисная неизвестная, и система оказывается приведенной к эквивалентной системе с базисом.
Применим описанный алгоритм к системе из примера.
| b | x1 | x2 | x3 | x4 | x5 | Доп.множитель. |
| 15(10) |  7
-1 7
-1
| -1 -6 | -1 -1 | -8 | -3 -1 | - -4 -2 |
| -12 57(-62) | -7 -31 |  -5
-19 -5
-19
| -2 | -2 -5 | -1 - -3 | |
| -40,5 28,5 0(-5) -57,5 | -22,5 15,5 -33,5 | -14,5 9,5 -19,5 | -4,5
2,5
 0
-4,5 0
-4,5
| 4,5 -2,5 - - | ||
| -31/9 115/9 | -28/9 67/9 | -4/3 19/3 |
Т.1
*
Т.2
*
*
Т.3
*
Т.4*
*
В Т.1 за главный элемент выбран коэффициент при x2 в 1-м уравнении. В Т.2 соответствующая строка помечена звездочкой в знак того, что в ней выбирался главный элемент. Затем эта строка умножается на соответствующие множители и добавляется к строкам исходной таблицы.
Дальнейшие действия аналогичны и понятны из приведенных таблиц.
В Т.З появляется строка, в которой все коэффициенты при неизвестных равны нулю.
Если в исходной таблице свободный член b3=10, то появилась противоречивая строка,
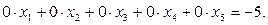 |
Следовательно, система не имеет решений.
Если же b3 = 15, то третья строка таблицы Т.З состоит из одних нулей и удаляется из таблицы.
Дальнейшее решение (Т.4) касается только этого случая.
В Т.4 все строки помечены звездочками, т.е. главный элемент появлялся, в каждой из них, и выбор его, более невозможен.
Работа алгоритма закончена. Т.4 дает запись системы с базисом, эквивалентной исходной:
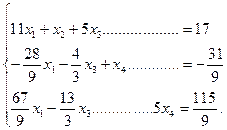
Общее решение последней, а значит, и исходной системы даете формулами:
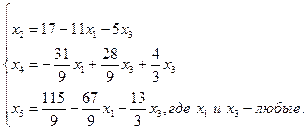
Например, при x1=1 и x3=1 получаем x,=1, x4=1, x5=1 т.е. получаем решение X=(1;1;1;1;1). Положив x1=x3=0 получаем базисное решение Xбаз.=(0;17;0;-31/9;ll5/9), В заключение этого пункта отметим, что метод Жордана позволяет полностью исследовать любую систему линейных алгебраических уравнений.
а) если в ходе вычислений появляется «противоречивая строка»
| b≠0 | …….. |
то система не имеет решений. Уравнение, отвечающее этой строке, противоречит уравнениям, строки которых помечены звездочками (т.е. в которых выделялся главный элемент);
б) если «противоречивая строка» в ходе вычислении не появлялась, то система имеет решение. Его общий вид получается из последней таблицы. Если есть свободные неизвестные, то система имеет бесконечно много решений. Если свободных переменных нет, то система имеет единственное решение;
в) появление нулевой строки показывает, что соответствующее ей уравнение является следствием уравнений, помеченных звездочками в данной таблице. Число независимых уравнений равно числу ненулевых строк последней таблицы (в случае разрешимости системы).
Указания к задаче 4
Задача 4. связана с действиями над матрицами. Для решения этой задачи следует использовать следующие сведения:
1. Всякая система m·n, расположенных в виде прямоугольной таблицы, содержащей
m строк и n столбцов, называется матрицей размера m×n и записывается в виде:
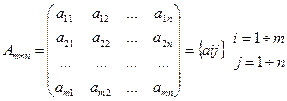
2). Матрица размера m×m (количество строчек равно количеству столбцов) называется квадратной матрицей порядка m.
3). Диагональ квадратной матрицы, идущая от левого верхнего утла к правому нижнему, называется главной диагональю, а вторая диагональ называется побочной.
4). Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные цифры нули, называется единичной матрицей n, обозначается следующим образом:
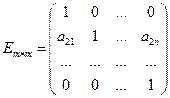
5) Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах, т.е. если
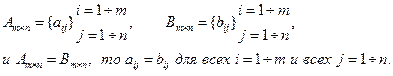
6). Произведением матрицы 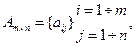
на число α называется матрица Cm×n, каждый элемент которой равен произведению соответствующего элемента матрицы Am×n на число α.
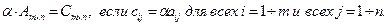
7). Суммой двух матриц одной размерности
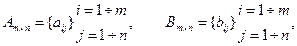 называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е.
называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е.
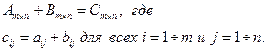
8). Умножение матрицы на матрицу
Пусть даны две матрицы Am×n и Bn×k, таких что число столбцов матрица А равно числу строк матрицы В. Тогда произведением матриц называется матрица Cm×k, каждый элемент которой cij равен сумме попарных произведений элементов i–й строки матрицы А на соответствующие элементы j-го столбца матрица В, т.е.

Заметим, что A·B≠B·A
9). Определители квадратных матриц
Каждой квадратной матрице ставится в соответствие число, обозначаемое
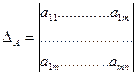 |
Рассмотрим определителя для матриц первого, второго и третьего порядков:
а). Пусть А=(а11), тогда ΔА=│a11│=a11. (1)
Из формулы (1) следует, что определитель для матрицы первого порядка совпадает с элементами матрицы А1·1.
б). Пусть (2)
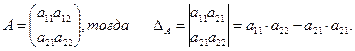
Из формулы (2) следует, что определитель для матрицы второго порядка, равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.
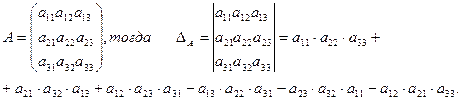
в). Пусть (3)
Формулу (3) запомнить значительно труднее, чем (1) и (2), но это и не требуется, так как существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.
Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2.

Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1, а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2.
10). Алгебраическим дополнением элемента аij квадратной матрицы Am×n называется число Аij, вычисляемое по формуле:
Aij=(-1)i+j·Mij, где Mij- определитель, полученный из определителя матрицы Am×n удалением строки с номером i и столбца с номером j .
11). Обратная матрица
Матрица А-1 называется обратной к матрице А, если A·A-1=A-1·A=E , где Е - единичная матрица. Из определения следует, что матрицы А и А-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от
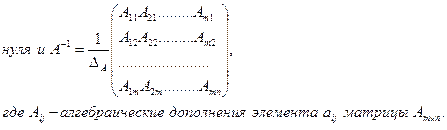
12). Решение простейших алгебраических уравнений
а) А·X=В, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X=А-1·В.
б) X·А=В, - где ,А и В заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X= А-1·X.
Примеры
1). Выполнить действия: (А+2В)·С, где
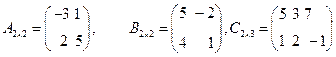
Решение
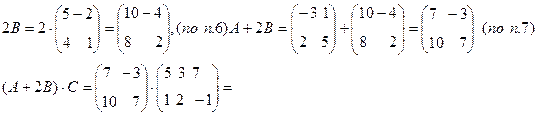
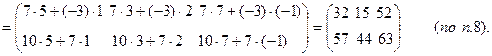
2). Найти А-1, если 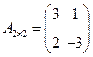
Решение
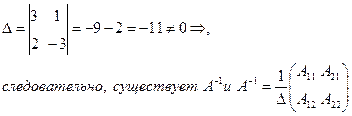
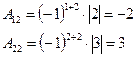
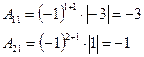
Тогда 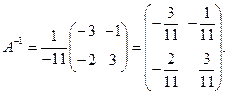
Проверим, верно ли нашли А-1. Для этого умножим А на А-1 и убедимся, что получим единичную матрицу.
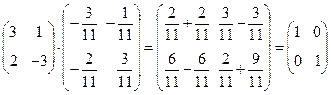
3). Решить уравнение AX-B=C, где
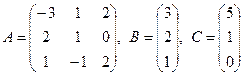
Решение
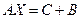
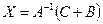
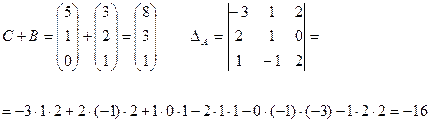
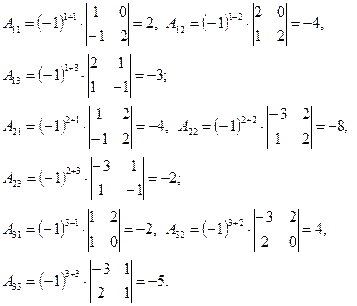
Тогда 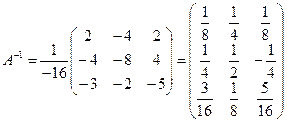
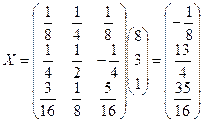
Проверка
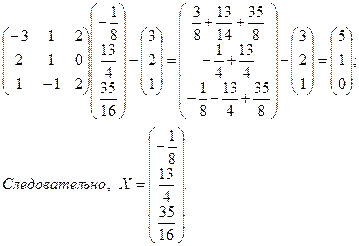
Контрольная работа №1
Задача 1
1.1. Прямая проходит через точку пересечения прямых 5x+2y+1=0 и 2x-3y+8=0 и параллельна прямой 7x+9y-8=0. Написать ее уравнение.
1.2. Точки А(-3;4) и В(4;5) являются противоположными вершинам ромба. Написать уравнения его диагоналей.
1.3. Найти проекцию точки А(2;-1) на прямую 4х+Зу-10=0.
1.4. На прямой Зх+2у-9=0 найти точку, равноудаленную от точек А(2;-1) и B(5;4).
1.5. Прямая проходит через середину отрезка АВ, где А(4;-1), В(3;5), и наклонена к оси ОХ под углом 2/3π. Найти ее уравнение.
1.6. При каком а прямые 4х + (3а+2)у+7 = 0 и 2ax-3у+7х+11=0 перпендикулярны друг другу?
1.7. Прямая проходит через точку пересечения прямых 3x-4y-18=0 и 5x+3y-1=0, и перпендикулярна прямой Зх+9y-7=О. Найти точки пересечения этой прямой с осями координат.
1.8. Точка А(1;-3) является вершиной трапеции, а прямая 4x+Зу-5=0, одним из ее оснований. Найти уравнение другого основания.
1.9. Найти точку, симметричную точке А(-5;-1) относительно прямой 4х+3y+8=0.
1.10. При каком значении а прямые 3ах+6y+2y+7=0 и 5x+(-7а)у+11=0 параллельны друг другу?
1.11. Точки А(2;-3) и В(1;4) являются противоположными вершинами ром6a, а прямая х+у+1=0 - уравнением одной из сторон Написать уравнения остальных сторон ромба.
1.12. Точки A(1;-3); В(5;2) и С(-4;1) являются вершинами ΔАBC. Написать уравнение высоты ВК этого треугольника.
1.13. В каком отношении прямая 3x+5y-10=О делит отрезок АВ, где A(2;-1), B(3;2)?
1.14. Прямая проходит через точку пересечения прямой 3х-4y+8=0 с осью OY и точку А(-3;2). Найти ее уравнение и угол наклона прямой к оси OX.
1.15. При каком значении m точка A(-4;2) принадлежит прямой (5m-3)x+4y-2m+1=0?
1.16. Прямая 5x+9y-1=0 является одной из сторон прямоугольника ABСD. Написать уравнение сторон этого прямоугольника, проходящих через вершину A(-3;2).
1.17. Написать уравнение прямой, параллельной оси OY и проходящей через точку пересечения медиан ΔАBC, если А(-1;2), В(3;5), С(1;8).
1.18. Даны уравнения двух сторон параллелограмма: х+у-1=0; 3x+4-у=0 и точка пересечения его диагоналей С(3;3). Найти уравнения двух других сторон параллелограмма.
1.19. Заданы уравнения средних линии ΔАBC х+у-1=0; 2х+3у-4=0; 3х+4у-1=0. Написать уравнения сторон этого треугольника.
1.20. В ΔАBC │АВ│=│BC│, точка А(-1;2), а прямая x+2у+7=0 является высотой BK этого треугольника. Найти координаты вершины С этого треугольника.
Задача 2.Решить графически систему неравенств и найти координаты вершин полученной области.
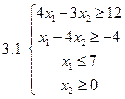
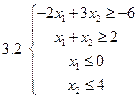
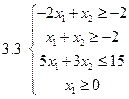
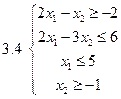
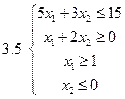
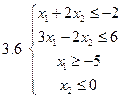
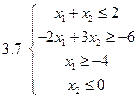
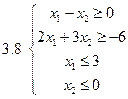
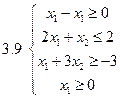
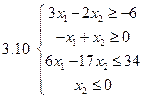
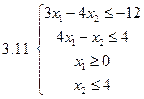
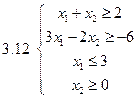
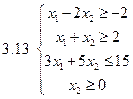
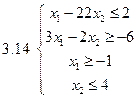
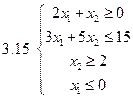
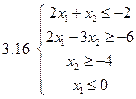
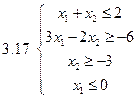
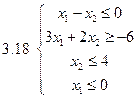
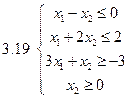
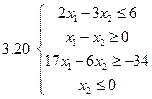
Задача 3.
3.1-3.20. Решить систему методом Жордано - Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.
3.1. 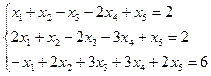
3.2. 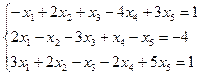
3.3. 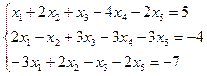
3.4. 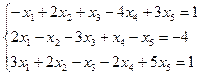
3.5. 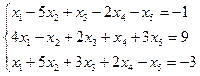
3.6. 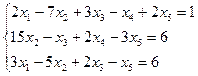
3.7. 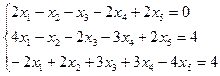
3.8. 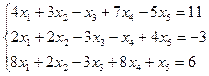
3.9. 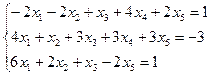
3.10. 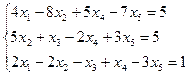
3.11. 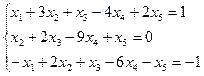
3.12. 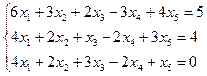
3.13. 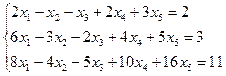
3.14. 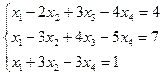
3.15. 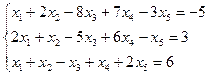
3.16. 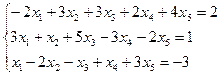
3.17. 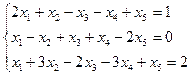
3.18. 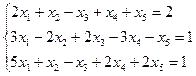
3.19. 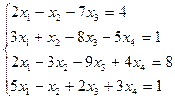
3.20. 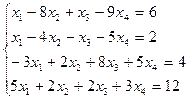
Задача 4.
4.1-4.20 Решить матричные уравнения и сделать проверку.
4.1. 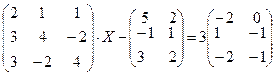
4.2. 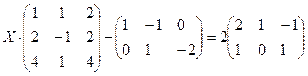
4.3. 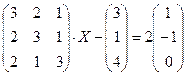
4.4. 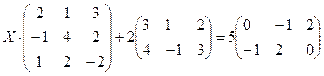
4.5. 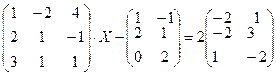
4.6. 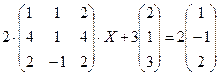
4.7. 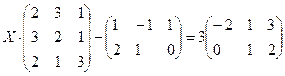
4.8. 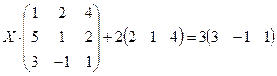
4.9. 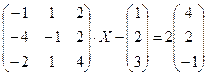
4.10. 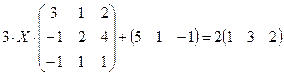
4.11. 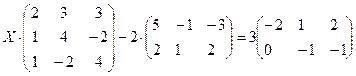
4.12. 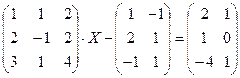
4.13. 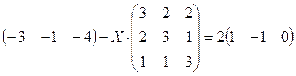
4.14. 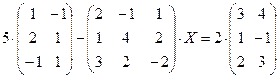
4.15. 
4.16. 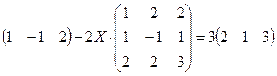
4.17. 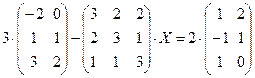
4.18. 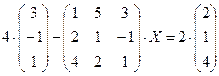
4.19. 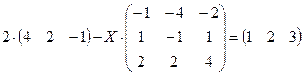
4.20. 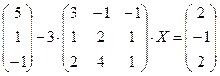
|
из
5.00
|
Обсуждение в статье: Преобразование не ключевых строк |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

