 |
Главная |
Исследование сходимости знакопеременных и знакочередующихся рядов
|
из
5.00
|
Пусть слагаемые числового ряда 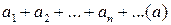 могут быть произвольного знака, такой ряд называется знакопеременным. Составим положительный ряд из модулей слагаемых
могут быть произвольного знака, такой ряд называется знакопеременным. Составим положительный ряд из модулей слагаемых 
Доказательство (см.[1-3]), что если сходится ряд (b), то ряд (a) тоже сходится, причем такая сходимость называется абсолютной. Если ряд (b) расходится, но ряд (a), сходится то такая сходимость называется неабсолютной (условной).
Пример 1.7
Исследовать сходимость ряда  .
.
Решение: Воспользуемся теоремой сравнения для ряда из модулей  Ряд
Ряд  сходится, поэтому исследуемый ряд сходится абсолютно.
сходится, поэтому исследуемый ряд сходится абсолютно.
Ответ: сходится абсолютно.
Частный случай знакопеременного ряда, когда положительные и отрицательные слагаемые строго чередуются друг за другом, называются знакочередующимся рядом. Такой ряд принято записывать в виде  где
где 
Доказано (см.[1-3]), что если знакочередующийся ряд удовлетворяет условиям:  , то он сходится, и его сумма не превосходит
, то он сходится, и его сумма не превосходит  (теорема Лейбница).
(теорема Лейбница).
Пример 1.8
Исследовать сходимость ряда 
Решение: Составим ряд из модулей  .
.
Так как 1/3<1, то он расходится, поэтому абсолютной сходимости у знакочередующегося ряда нет. Оба условия теоремы Лейбница выполнены:
 .
.
Ответ: знакочередующийся ряд сходится неабсолютно (условно).
Дифференциальные уравнения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую x, искомую функцию y и ее производные или дифференциалы.
Символически дифференциальное уравнение записывается так :  .
.
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

Для решения этого уравнения нужно сначала разделить переменные :
 ,
,
а затем проинтегрировать обе части полученного равенства :
 .
.
Найти общее решение уравнения :  .
.
Разделив переменные имеем :  , интегрируем обе части уравнения:
, интегрируем обе части уравнения:


Так как производная постоянная, то для удобства дальнейших преобразований вместо С можно писать  .Потенцируя, последнее равенство, получим
.Потенцируя, последнее равенство, получим  . Это и есть общее решение данного уравнения
. Это и есть общее решение данного уравнения
Контрольная работа № 3
Задание 1
1.1-1.20 Вычислить неопределенные интегралы, результат проверить дифференцированием:
1.1. а).  b)
b)  c)
c) 
1.2. а)  b)
b)  c)
c) 
1.3. а)  b)
b)  с)
с) 
1.4. а)  b)
b) 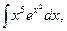 c)
c) 
1.5. а)  b)
b)  c)
c) 
1.6. а)  b)
b) 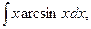 c)
c) 
1.7. а)  b)
b)  c)
c) 
1.8. а)  b)
b)  c)
c) 
1.9. а)  b)
b)  c)
c) 
1.10. а)  b)
b)  c)
c) 
1.11. а)  b)
b)  c)
c) 
1.12. а) 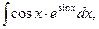 b)
b)  c)
c) 
1.13. а)  b)
b)  c)
c) 
1.14. а) 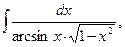 b)
b)  c)
c) 
1.15. а)  b)
b)  c)
c) 
1.16. а)  b)
b)  c)
c) 
1.17. а)  b)
b)  c)
c) 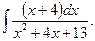
1.18. а)  b)
b)  c)
c) 
1.19. а)  b)
b)  c)
c) 
1.20 а)  b)
b)  c)
c) 
Задание 2
2.1.- 2.20. – Вычислить определенный интеграл
2.1. 
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 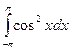
2.7. 
2.8. 
2.9. 
2.10. 
2.11. 
2.12. 
2.13. 
2.14. 
2.15. 
2.16. 
2.17. 
2.18. 
2.19. 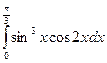
2.20. 
Задание 3.
3.1 -3.7 Вычислить площади фигур, ограниченных следующими линиями:
3.1. 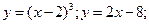
3.2. 
3.3. 
3.4. 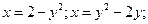
3.5. 
3.6. 
3.7. 
3.8-3.12 Вычислить длины дуг кривых, заданных уравнениями:
3.8. 
3.9. 
3.10. 
3.11. 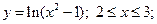
3.12. 
3.13-3.16 Вычислить объем тел, образованных вращением фигур, ограниченных графиками функций, вокруг оси  :
:
3.13. 
3.14. 
3.15. 
3.16. 
3.17-3.20 Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций, вокруг оси  :
:
3.17. 
3.18. 
3.19. 
3.20. 
Задание 4.Найти сумму ряда (или доказать его расходимость)
4.1. 
4.2. 
4.3. 
4.4. 
4.5. 
4.6. 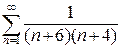
4.7. 
4.8. 
4.9. 
4.10. 
4.11. 
4.12. 
4.13. 
4.14. 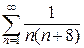
4.15. 
4.16. 
4.17. 
4.18. 
4.19. 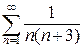
4.20. 
Задание 5. Найти общее решение или общий интеграл дифференциального уравнения:
5.1. 
5.2. 
5.3. 
5.4. 
5.5. 
5.6. 
5.7. 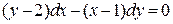
5.8. 
5.9. 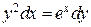
5.10. 
5.11. 
5.12. 
5.13. 
5.14. 
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 
Информационные ресурсы дисциплины:
Основная:
1. Кремер Н.Ш. Высшая математика для экономических специальностей :учебник и практикум -3е издание, перераб. И доп.-М.: Юрайт,2011-909с.
2. Лунгу К.Н. Сборник задач по высшей математике. 1 курс-8-е издание.-М.: Айрис-пресс,2009,576с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление : учебник для вузов в 2-х томах.М.: Интеграл-Пресс,2009-416 с.
Дополнительная:
1.Шипачев В.С. Высшая математика : Учебник для вузов -6-е издание.-М.: Высшая школа,2003-479с.
2.Виленкин И.В.Высшая математика для студентов экономических, технических,естественно-научных специальностей вузов.-Ростов-на-Дону,Феникс,2002-416с.
3.Данко П.Е.,Попов.А.Г.,Кожевникова Т.Я.-М.:Оникс 21 век, Мир и образование,2003
4.Шипачев В.С. Математический анализ : Учебное пособие для вузов-М.: Высшая школа,2001.-176с.
Электронные ресурсы:
1. Библиотека ГУАП – http://www.lib.aanet.ru
2. Научная библиотека Elibrary – http://wwwelibrary.ru
|
из
5.00
|
Обсуждение в статье: Исследование сходимости знакопеременных и знакочередующихся рядов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

