 |
Главная |
Альтернативный оптимум
|
из
5.00
|
Задача № 3.3.
Решить симплексным методом задачу
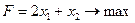 (3.21)
(3.21)
 (3.22)
(3.22)
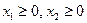 .
.
Решение.
Для решения поставленной задачи симплексным методом от стандартной формы записи задачи ЛП перейдем к канонической. Ведем балансовые переменные  :
:
 (3.23)
(3.23)
Составим расширенную матрицу системы :


По теореме Кронекера - Капелли система (3.23) совместна и имеет бесчисленное множество решений.
Так как ранг системы (3.23) равен двум, то базисных переменных будет ровно две. На первом шаге в качестве базисных переменных удобно взять балансовые переменные  , так как система (3.23) легко разрешима относительно этих переменных.
, так как система (3.23) легко разрешима относительно этих переменных.
I.  - базисные переменные;
- базисные переменные;
 - свободные переменные.
- свободные переменные.
Систему (3.23) решим относительно базисных переменных:
 (3.24)
(3.24)
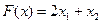 . (3.25)
. (3.25)
Обнулив свободные переменные, получим опорное решение:
 ;
; 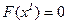 . Решение
. Решение 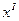 на данном шаге не является оптимальным, т.к. возможно дальнейшее увеличение целевой функции за счет введения в базис свободных переменных
на данном шаге не является оптимальным, т.к. возможно дальнейшее увеличение целевой функции за счет введения в базис свободных переменных  . Введем в базис переменную
. Введем в базис переменную 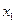 . Так как
. Так как  , то второе уравнение в системе (3.24) будет разрешающим. Выведем из базиса переменную
, то второе уравнение в системе (3.24) будет разрешающим. Выведем из базиса переменную  .
.
II.  - базисные переменные;
- базисные переменные;
 - свободные переменные.
- свободные переменные.
Запишем выражения для базисных переменных и целевой функции через свободные переменные:
 (3.26)
(3.26)
 . (3.27)
. (3.27)
 - опорное решение;
- опорное решение;  . Дальнейшее увеличение целевой функции невозможно, так как в выражении целевой функции через свободные переменные (3.27) отсутствуют положительные коэффициенты при свободных переменных. Следовательно, критерий оптимальности выполнен,
. Дальнейшее увеличение целевой функции невозможно, так как в выражении целевой функции через свободные переменные (3.27) отсутствуют положительные коэффициенты при свободных переменных. Следовательно, критерий оптимальности выполнен,  - оптимальное решение исходной задачи.
- оптимальное решение исходной задачи.
Заметим, что в последнем выражении целевой функции через свободные переменные (3.27) отсутствует свободная переменная 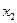 (можно сказать, что входит с нулевым коэффициентом). В связи с чем, изменение переменной
(можно сказать, что входит с нулевым коэффициентом). В связи с чем, изменение переменной 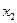 не повлечет за собой значения целевой функции. Например, переменную
не повлечет за собой значения целевой функции. Например, переменную 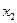 введем в базисные переменные. В системе (3.26) разрешающим для переменной
введем в базисные переменные. В системе (3.26) разрешающим для переменной 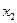 является второе уравнение (
является второе уравнение (  ). Выведем переменную
). Выведем переменную 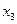 из базиса, получим:
из базиса, получим:
 , (3.28)
, (3.28)
 .
.
Обнулив свободные переменные, получим опорное решение:
 ;
;  .
.
В двух соседних вершинах области допустимых решений, при изменении 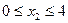 , мы получили одно и то же значение целевой функции -
, мы получили одно и то же значение целевой функции -  , которое невозможно в данной задаче увеличить.
, которое невозможно в данной задаче увеличить.
Для того, чтобы записать оптимальное решение, воспользуемся системой (3.26). Положим  , где
, где  . В системе (3.26) переменная
. В системе (3.26) переменная  является свободной и в базисном решении
является свободной и в базисном решении  . Отсюда
. Отсюда  ;
;  .
.
Ответ. 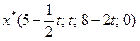 ,
,  .
.
Задачи для самостоятельного решения
Задача № 3.4.
Задачу ЛП решить симплексным методом:

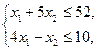
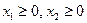 .
.
Задача № 3.5.
Задачу ЛП решить симплексным методом:

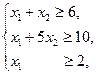
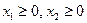 .
.
Задача № 3.6.
Решить симплексным методом задачу № 1.2.
Задача № 3.7.
Решить симплексным методом задачу № 1.11.
Задача № 3.8.
Решить симплексным методом задачу № 2,7.
Задача № 3.9.
Решить симплексным методом задачу № 1.19.
Задача № 3.9.
Решить симплексным методом задачу № 2.6.
|
из
5.00
|
Обсуждение в статье: Альтернативный оптимум |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

