 |
Главная |
Расчет числа независимых условных уравнений
|
из
5.00
|
При уравнивании несвободной сети триангуляции по углам (для сети на рис.1.1) число независимых условных уравнений определяется по формулам:
| Всего уравнений: В том числе: | 
| = 18+1+0-2·5 = 19-10 = 9, |
| Фигур | 
| = 18 –12 – 1 +1 = 6, |
| Горизонта | 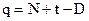
| = 18 + 7 – 24 = 25 – 24 = 1, |
| Полюсных | 
| = 12 –2·7+3 = 12-14+3 = 1, |
| Базисных | 
| = 2 - 1 = 1, |
| Дирекционных углов | 
| = 1 – 1 = 0, |
| Координат | 
| = 2·(1-1) = 0. |
где N = 18 – общее число измеренных в сети углов ;
 = 1 – число дополнительно измеренных сторон;
= 1 – число дополнительно измеренных сторон;
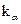 = 0 - число дополнительно измеренных азимутов (дирекционных углов);
= 0 - число дополнительно измеренных азимутов (дирекционных углов);
 = 5 – число определяемых пунктов;
= 5 – число определяемых пунктов;
 = 12 – число всех сторон в сети (исходных и определяемых);
= 12 – число всех сторон в сети (исходных и определяемых);
 = 1 – число условий горизонта;
= 1 – число условий горизонта;
 = 7 – число пунктов, на которых выполнены угловые измерения;
= 7 – число пунктов, на которых выполнены угловые измерения;
 = 24 – число измеренных в сети направлений;
= 24 – число измеренных в сети направлений;
 = 7 – число всех пунктов в сети;
= 7 – число всех пунктов в сети;
 = 2 - число всех исходных (вычисленных по координатам и дополнительно измеренных) сторон;
= 2 - число всех исходных (вычисленных по координатам и дополнительно измеренных) сторон;
 = 1 – число всех исходных (вычисленных по координатам и дополнительно измеренных) азимутов (дирекционных углов);
= 1 – число всех исходных (вычисленных по координатам и дополнительно измеренных) азимутов (дирекционных углов);
 =1 – число раздельных групп исходных пунктов, не связанных между собой исходными сторонами.
=1 – число раздельных групп исходных пунктов, не связанных между собой исходными сторонами.
Угловые условия (фигур, горизонта, азимутов)
К угловым условиям, возникающим в сети триангуляции при уравнивании углов, относят условия фигур, горизонта иазимутов (дирекционных углов).
Условие фигуры возникает в многоугольнике и соответствует формуле для суммы его внутренних углов  , где
, где 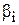 - значения углов, i=1,…, К; К – количество углов многоугольника. Условное уравнение поправок имеет вид
- значения углов, i=1,…, К; К – количество углов многоугольника. Условное уравнение поправок имеет вид  , где
, где  - поправка к
- поправка к  ;
;  - свободный член K – ого условного уравнения, j - количество измеренных углов в треугольнике.
- свободный член K – ого условного уравнения, j - количество измеренных углов в треугольнике.
В примере (рис.1.1) возникают шесть условий фигур (не перекрывающихся треугольников), которые имеют вид:
V1 + V2 + V3 + W1= 0,
V4 + V5 + V6 + W2 = 0,
V7 + V8 + V9 + W3 = 0,
V10 + V11 + V12 + W4= 0,
V13 + V14 + V15 + W5 = 0,
V16 + V17 + V18 + W6 =0.
Свободные члены условий фигур равны невязкам соответствующих треугольников (см. табл. 8)  , к = 1, …, 6.
, к = 1, …, 6.
Условие горизонта возникает на тех пунктах, на которых включают в уравнивание все углы, образованные всеми парами смежных направлений. Особенностью этого условия является то, что сумма измеренных значений углов равна точно  , т.е. невязки этих условий всегда равны нулю. Для нашего случая условие горизонта можно записать в виде (табл.14)
, т.е. невязки этих условий всегда равны нулю. Для нашего случая условие горизонта можно записать в виде (табл.14)
 , где
, где  .
.
Таблица 11
Условие горизонта на пункте 7
| Угол | Значение угла | ||
| 13,9 | |||
| 10,3 | |||
| 35,9 | |||
| 46,7 | |||
| 57,0 | |||
| 16,2 | |||
| W7= | 0,00 | ||
| W7доп= | 30,62” |
Допустимые величины свободных членов вычисляются по формуле  , где К - число углов в уравнении.
, где К - число углов в уравнении.
Условие азимутов (дирекционных углов) возникает в сети, если имеются две или более сторон с известными азимутами (дирекционными углами). В нашем примере условие дирекционных углов не возникает, поскольку известен дирекционный угол только одной стороны 2-3.
Полюсное условие
По своему варианту определяют фигуры, которые имеют полюсные условия (геодезический четырехугольник, центральная система), составляют полюсные условные уравнения, вычисляют свободные члены и их допустимые значения.
Для примера сети , представленной на рис. 1.1 , полюсное условное уравнение центральной системы с полюсом в пункте 7, соответствующее условию (8), имеет вид:

Вычисления коэффициентов уравнения и свободного члена были выполнены в таблице 9.
Базисное условие
Для примера сети , представленной на рис. 1, базисное условное уравнение, соответствующее условию (9), имеет вид:

Вычисления коэффициентов уравнения и свободного члена были выполнены в таблице 10 .
|
из
5.00
|
Обсуждение в статье: Расчет числа независимых условных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

