 |
Главная |
Силовое воздействие потока пара на рабочие лопатки
|
из
5.00
|
При работе турбины со стороны пара на лопатки действуют аэродинамические силы. Поставим задачу: определить величину и направление силы, действующей на одну лопатку. Для решения этой задачи сделаем допущения: 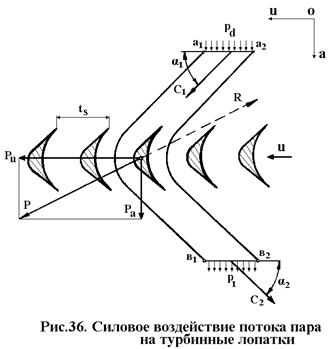
1. Вместо реального лопаточного венца рассматриваем плоскую бесконечную решетку профилей.
2. Поток пара, обтекающий данную решетку, считаем установившимся и простирающимся на бесконечность перед решеткой и за ней.
3. Пренебрегаем силами вязкости по сравнению с силами инерции частиц пара.
Рассмотрим плоскую решетку профилей рабочих лопаток, обтекаемую потоком пара (рис.36). Выделим в потоке контрольный объем, ограниченный по высоте длиной рабочих лопаток ls, двумя боковыми поверхностями, проходящими через линии тока а1в1 и а2в2 и отстоящим друг от друга на расстоянии ts, называемом шагом рабочих лопаток, и двумя сечениями а1а2 и в1в2, параллельными плоскости вращения ротора турбинной ступени. Один из профилей полностью находится внутри контрольного объема. Так как поверхности а1в1 и а2в2 являются поверхностями тока, то они для потока будут непроницаемыми (нет протечек пара).
В соответствии с принятыми допущениями о бесконечности потока перед решеткой и за ней скорости и давления в каждой точке сечений а1а2 и в1в2 будут одинаковыми.
Таким образом, в сечении а1а2 имеем скорость пара С1 и давление Рd, а в сечении в1в2 – скорость пара С2 и давление Р1.
Поворот и ускорение потока в межлопаточном канале рабочей решетки вызывается действием рабочих лопаток на поток пара и разностью давлений рd и р1 на входе и выходе из канала. Пусть равнодействующая сил, действующих на контрольный объем со стороны профиля (лопатки), равна вектору 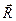 с направлением, показанным на рис. . Очевидно, если лопатка воздействует на поток с силой
с направлением, показанным на рис. . Очевидно, если лопатка воздействует на поток с силой 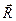 , то поток действует на лопатку с силой
, то поток действует на лопатку с силой 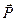 , равной по величине и противоположной по направлению силе
, равной по величине и противоположной по направлению силе 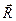 . Как раз сила
. Как раз сила 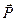 и создает момент, вызывающий движение лопатки с окружной скоростью и и, как результат, вращение ротора турбины с угловой скоростью ω.
и создает момент, вызывающий движение лопатки с окружной скоростью и и, как результат, вращение ротора турбины с угловой скоростью ω.
Спроектируем вектор силы 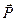 на окружное (в направлении окружной скорости и) и осевое (ось вращения ротора) направления. Из рассмотрения рис.36 следует, что полезная работа, обеспечивающая движение лопаток и вращение ротора, создается только окружной составляющей силы
на окружное (в направлении окружной скорости и) и осевое (ось вращения ротора) направления. Из рассмотрения рис.36 следует, что полезная работа, обеспечивающая движение лопаток и вращение ротора, создается только окружной составляющей силы 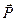 , которая обозначена
, которая обозначена 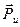 , так как направление этой составляющей совпадает с направлением движения лопатки (профиля). Осевая составляющая силы
, так как направление этой составляющей совпадает с направлением движения лопатки (профиля). Осевая составляющая силы 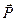 , обозначаемая Ра, направлена перпендикулярно плоскости вращения, поэтому эта составляющая полезной работы не совершает. Воздействуя через лопатки на ротор, составляющая Ра вызывает перемещение ротора вдоль оси турбины. Равнодействующая всех сил Ра воспринимается упорным подшипником турбины. Если бы последний в турбине отсутствовал, то осевое перемещение ротора привело бы к опасному уменьшению осевых зазоров в проточной части турбины, задеванию подвижных частей о неподвижные и, в конечном счете, к аварии турбины. При проектировании турбины стремятся иметь составляющую Ра как можно меньшей. В противном случае это повлечет за собой более громоздкую конструкцию упорного подшипника, а надежность его работы будет ухудшена из-за возможности выплавления белого металла.
, обозначаемая Ра, направлена перпендикулярно плоскости вращения, поэтому эта составляющая полезной работы не совершает. Воздействуя через лопатки на ротор, составляющая Ра вызывает перемещение ротора вдоль оси турбины. Равнодействующая всех сил Ра воспринимается упорным подшипником турбины. Если бы последний в турбине отсутствовал, то осевое перемещение ротора привело бы к опасному уменьшению осевых зазоров в проточной части турбины, задеванию подвижных частей о неподвижные и, в конечном счете, к аварии турбины. При проектировании турбины стремятся иметь составляющую Ра как можно меньшей. В противном случае это повлечет за собой более громоздкую конструкцию упорного подшипника, а надежность его работы будет ухудшена из-за возможности выплавления белого металла.
Для определения полезной работы на окружности Lи турбинной ступени и расчетов упорного подшипника необходимо уметь вычислять значения составляющих Ри и Ра, аналитические выражения которых могут быть получены следующим образом.
Применим к выделенному контрольному объему теорему об изменения количества движенияв следующей формулировке:
Приращение количества движения пара, содержащегося в контрольном объеме, равно импульсу внешних сил, действующих на этот объем:
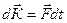 (5.1)
(5.1)
где 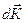 – изменение количества движения пара, содержащегося в контрольном объеме, за промежуток время dt;
– изменение количества движения пара, содержащегося в контрольном объеме, за промежуток время dt;
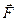 – главный вектор внешних сил, действующих на контрольный объем.
– главный вектор внешних сил, действующих на контрольный объем.
Перепишем выражение (5.1) в виде:
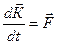 (5.2)
(5.2)
и подсчитаем вначале скорость изменения количества движения.
Прежде всего, обратим внимание на то, что рассматривается установившееся движение пара и поэтому 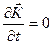 (5.3)
(5.3)
Поэтому количество движения пара в контрольном объеме может изменяться только за счет того, что пар втекает в объем и вытекает из него. Однако поверхности а1а2 и в1в2 являются по условию поверхностями тока и потому непроницаемы для потока. Следовательно, пар втекает в контрольный объем через сечение а1в1 и вытекает из него через сечение а2в2. Таким образом:
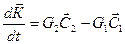 (5.4)
(5.4)
где G1 и G2 – расход пара через сечения а1в1 и а2в2.
При установившемся движении
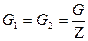 (5.5)
(5.5)
где G – расход пара через венец рабочих лопаток;
Z – общее число рабочих лопаток.
Таким образом:
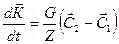 (5.6)
(5.6)
Спроектируем равенство (5.6) на координатные оси, выбрав направление осей следующим образом: ось «и» совпадает с направлением окружной скорости, ось «а» совпадает с направлением оси турбины. Тогда получим:
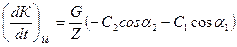 (5.7)
(5.7)
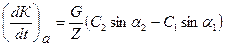 (5.8)
(5.8)
Обратим внимание на знак «минус» перед выражением С2соsα2 (5.7). Этот знак появляется в результате того, что угол α2 отсчитывается от отрицательного направления оси «и».
Теперь определим главный вектор внешних сил 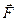 . При подсчете внешних сил будем пренебрегать массовыми силами: силы трения являются внутренними и при подсчете
. При подсчете внешних сил будем пренебрегать массовыми силами: силы трения являются внутренними и при подсчете 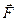 учитываться не должны. Тогда из числа внешних сил, действующих на контрольный объем остаются силы давления по границам объема и силы
учитываться не должны. Тогда из числа внешних сил, действующих на контрольный объем остаются силы давления по границам объема и силы 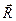 реакции лопатки на поток. Таким образом:
реакции лопатки на поток. Таким образом:
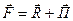 (5.9)
(5.9)
где через 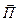 обозначаем сумму сил давления на границах контрольного объема.
обозначаем сумму сил давления на границах контрольного объема.
Заметим, что искомая сила 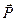 , действующая со стороны потока на лопатку, равна по величине и противоположна по направлению реакции лопатки
, действующая со стороны потока на лопатку, равна по величине и противоположна по направлению реакции лопатки 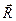 , т.е.
, т.е.
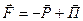 (5.10)
(5.10)
Спроектируем равенство (2.5.10) на окружное и осевое направление. При подсчете проекций вектора 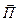 , обратим внимание, что силы давлений на поверхностях тока а1а2 и в1в2 равны по величине и противоположны по направлению, так как эти поверхности тока расположены на расстоянии одного шага. Поэтому силы давлений на поверхностях а1а2 и в1в2 взаимно уравновешивают друг друга. Следовательно, при подсчете проекций
, обратим внимание, что силы давлений на поверхностях тока а1а2 и в1в2 равны по величине и противоположны по направлению, так как эти поверхности тока расположены на расстоянии одного шага. Поэтому силы давлений на поверхностях а1а2 и в1в2 взаимно уравновешивают друг друга. Следовательно, при подсчете проекций 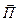 необходимо учитывать только силы давления в сечениях а1в1 и а2в2. Но эти сечения нормальны оси турбины, и потому проекция сил давления на окружное направление равна нулю, а проекция сил давления на осевое направление равна абсолютной величине этих сил.
необходимо учитывать только силы давления в сечениях а1в1 и а2в2. Но эти сечения нормальны оси турбины, и потому проекция сил давления на окружное направление равна нулю, а проекция сил давления на осевое направление равна абсолютной величине этих сил.
Таким образом:
Fu = – Рu (5.11)
Fa = – Рa + tℓs(Pd – Р1) (5.12)
Приравнивая (5.7) и (5.11), найдем окружную составляющую силы Р:
Рu = 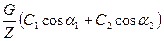 (5.13)
(5.13)
или Рu = 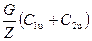 (5.14)
(5.14)
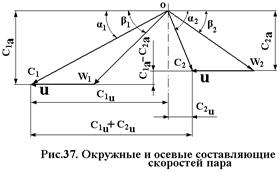
где 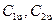 – окружные составляющие скоростей С1 и С2 (рис.37).
– окружные составляющие скоростей С1 и С2 (рис.37).
Приравнивая (2.5.8) и (2.5.12), найдем осевую составляющую силы Ра:
Ра = 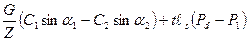 (5.15)
(5.15)
или Ра = 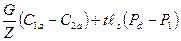 (5.16)
(5.16)
где 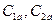 – осевые составляющие скоростей
– осевые составляющие скоростей 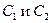 (рис.37).
(рис.37).
Полная величина силы Р определяется выражением:
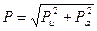 (5.17)
(5.17)
 Итак, поставленная задача решена – мы определили силу, с которой поток пара действует на турбинную лопатку.
Итак, поставленная задача решена – мы определили силу, с которой поток пара действует на турбинную лопатку.
На практике нас больше интересует окружная сила Рu, совершающая полезную работу, вращая ротор турбины. Осевая сила Ра никакой работы не совершает; стремится сдвинуть ротор турбины и требует разгрузки.
При подсчете сил Рu и Ра используются треугольники скоростей (рис.37). Сумма окружных составляющих скоростей 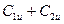 и разность осевых составляющих
и разность осевых составляющих 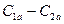 могут быть сняты непосредственно с треугольников скоростей.
могут быть сняты непосредственно с треугольников скоростей.
Работа окружной силы Рu будет подробно рассмотрена в следующем вопросе; здесь остановимся на характеристике силы Ра. Заметим, что первое слагаемое, входящее в выражение (5.16) по абсолютной величине невелико, а знак его зависит от знака разности 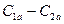 , в частном случае его значение может быть равно нулю. Величина второго слагаемого зависит от типа ступени.
, в частном случае его значение может быть равно нулю. Величина второго слагаемого зависит от типа ступени.
В активных ступенях Рd = Р1, и потому значение второго слагаемого равно нулю. В реактивных ступенях Рd > Р1, и потому осевая сила может достигать значительной величины.
|
из
5.00
|
Обсуждение в статье: Силовое воздействие потока пара на рабочие лопатки |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

