 |
Главная |
Особенности расчета внецентренно сжатых элементов прямоугольного сечения (случай I, большие эксцентриситеты)
|
из
5.00
|
На основании многочисленных экспериментов установлено, что величина разрушающего усилия зависит от величины эксцентриситета e0.
При действии продольной силы с малым эксцентриситетом или при сильной растянутой арматуре сечение элемента может оказаться полностью сжатым или иметь незначительную растянутую зону. Соответственно арматура А’s сжата, а арматура Аs, расположенная у грани, более удаленной от продольной силы, может быть и сжатой, и растянутой. Разрушение элемента в этом случае начинается со стороны сжатой зоны, что отвечает условию x>xR.(рис)

При загружении элемента продольной силой с большим эксцентриситетом или при наличии в растянутой зоне не очень сильной арматуры разрушение начинается со стороны растянутой грани сечения. Вначале появляются трещины в растянутом бетоне, которые по мере увеличения напряжений в арматуре раскрываются все шире; нейтральная ось перемещается ближе к сжатой грани.
Когда в растянутой арматуре достигается предел текучести, начинается разрушение элемента, вызванное достижением предельных сопротивлений в сжатом бетоне и сжатой арматуре. Такой вид разрушения внецентренно сжатых элементов наблюдается при относительной высоте сжатой зоны x£xR.

Таким образом, на основании опытов различают два основных случая разрушения внецентренно сжатых элементов:
1. Первый случай (случай больших эксцентриситетов), когда напряженное состояние приближается к изгибу и определяется в предельном состоянии достижением расчетного сопротивления в растянутой арматуре и сжатом бетоне.
2. Второй случай (случай малых эксцентриситетов), когда напряженное состояние приближается к центральному сжатию и определяется в предельном состоянии достижением расчетного сопротивления в сжатом бетоне.
Границей между этими двумя случаями является граница переармирования или условие прочности сжатой зоны для изгибаемых элементов.
В общем случае для сечений, имеющих по крайней мере одну ось симметрии и эксцентриситет в плоскости, проходящей через эту ось:при x£xR - первый случай (случай больших эксцентриситетов);при x>xR - второй случай (случай малых эксцентриситетов
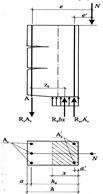
В общем случае расчет внецентренно сжатых железобетонных элементов проводят в третей стадии напряженно-деформированного состояния, составляя при этом следующие уравнения равновесия:SM = 0; SNх = 0.
M = N × e £ Rb×Ab×(h0 - x/2) + Rsc×As’×(h0 – a’); N £ Rb×Ab + Rsc×As’ - ss×As
Случай 1 (при x£xR - случай больших эксцентриситетов).

Уравнения равновесия примут вид:
M = N × e £ Rb×b×x×(h0 - x/2) + Rsc×As’×(h0 – a’); N £ Rb× b×x + Rsc×As’ - Rs×As где e = e0 + h/2 – a.
При симметричном армировании As = As’ и Rs = Rsc ; N £ Rb× b×x
Случай 2 (при x>xR - случай малых эксцентриситетов).

Уравнения равновесия примут вид: M = N × e £ Rb×Ab×(h0 - x/2) + Rsc×As’×(h0 – a’);
N £ Rb×Ab + Rsc×As’ - ss×As
где для элементов из бетона класса В30 и ниже с ненапрягаемой арматурой классов А-I, А-II, А-III ss определяется по эмпирической формуле: Gs=(2*1-x/ho/1-Еr -1)Rs
|
из
5.00
|
Обсуждение в статье: Особенности расчета внецентренно сжатых элементов прямоугольного сечения (случай I, большие эксцентриситеты) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

