 |
Главная |
Основные положения теории колебаний осцилляторов
|
из
5.00
|
1.1.1. Уравнения колебаний гармонического осциллятора
В колебательном процессе наблюдается определенная повторяемость во времени динамических переменных, характеризующих состояние колебательной системы. Если некоторая динамическая переменная s(t) повторяется через равные промежутки времени T (т.е. если s(t) = s(t+nT) для любого значения t, где n = 1, 2, 3 …), то говорят, что данная переменная совершает периодические колебания. Колебательная система как материальный объект называется осциллятором, если динамические переменные системы изменяются по некоторому периодическому закону. Колебательный процесс совершается, разумеется, осциллятором как материальным объектом, однако описание этого процесса осуществляется посредством законов изменения динамических переменных, характеризующих этот осциллятор. В этой связи будут использоваться выражения типа: «Координата (импульс, энергия …и т.п.) колеблется по закону …».
Промежуток времени T называется периодом колебания динамической переменной s(t) осциллятора. Пусть за время t совершено N полных колебаний. Число колебаний за единицу времени  называется частотойпериодического колебания. Так как при периодических колебаниях t = N T, то
называется частотойпериодического колебания. Так как при периодических колебаниях t = N T, то 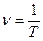 . Единица частоты n имеет собственное название – герц (Гц): 1Гц = 1 с-1.
. Единица частоты n имеет собственное название – герц (Гц): 1Гц = 1 с-1.
Важным частным случаем периодических колебаний являются гармонические колебания, т.е. колебания, совершаемые по закону синуса (косинуса): s(t) = A cos [a(t)], где a(t) – фаза колебания динамической переменной s(t). Соответствующая колебательная система называется гармоническим осциллятором. Примером гармонического колебания динамической переменной является колебание координаты материальной точки, которая равномерно движется по окружности (рис.1-1).
 Пусть материальная точка движется равномерно по окружности против часовой стрелки. Положение материальной точки можно задать или радиус-вектором A, или соответствующими координатами{x, y}.Допустим, в начальный момент времени радиус-вектором A повернут относительно оси ОХ наугол j. При равномерном вращении угловую скорость радиус-вектора можно определить как отношение полного угла поворота (a = 2p радиан) к периоду вращения T, т. е. w =
Пусть материальная точка движется равномерно по окружности против часовой стрелки. Положение материальной точки можно задать или радиус-вектором A, или соответствующими координатами{x, y}.Допустим, в начальный момент времени радиус-вектором A повернут относительно оси ОХ наугол j. При равномерном вращении угловую скорость радиус-вектора можно определить как отношение полного угла поворота (a = 2p радиан) к периоду вращения T, т. е. w = 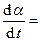
 . За время t радиус-вектор повернется на угол wt. Из рисунка видно, что текущие координаты x и y со временем изменяются по гармоническому закону:
. За время t радиус-вектор повернется на угол wt. Из рисунка видно, что текущие координаты x и y со временем изменяются по гармоническому закону:
x(t) = A cos(wt + j) и y(t) = A sin(wt + j), (1)
В уравнениях (1) А – амплитуда колебания координаты, т.е. максимального отклонения координаты от нулевого значения. Амплитуда – всегда положительна, а при гармонических колебаниях – еще и постоянна.
Величина w называется циклической частотой и характеризует быстроту изменение фазы колебания a(t) = (wt + j) в единицу времени, т.к.  . Фаза гармонического колебания a(t) = (wt + j) определяет значение колеблющейся физической величины в данный момент времени t. При гармонических колебаниях (w =
. Фаза гармонического колебания a(t) = (wt + j) определяет значение колеблющейся физической величины в данный момент времени t. При гармонических колебаниях (w = 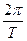 = 2pn). Единицей циклической частоты служит 1
= 2pn). Единицей циклической частоты служит 1  . Так как угол – безразмерная величина, то можно записать: 1
. Так как угол – безразмерная величина, то можно записать: 1  = 1с-1. Не следует путать циклическую частоту w с частотой n как числа колебаний в единицу времени. Например, если w = 10 с-1, то это означает, что за 1 с фаза колебания изменяется на 10 радиан, а величина n = 10 с-1 = 10 Гц указывает, что за секунду совершается 10 полных колебаний.
= 1с-1. Не следует путать циклическую частоту w с частотой n как числа колебаний в единицу времени. Например, если w = 10 с-1, то это означает, что за 1 с фаза колебания изменяется на 10 радиан, а величина n = 10 с-1 = 10 Гц указывает, что за секунду совершается 10 полных колебаний.
Время T приобретает смысл периода колебаний координат, т.е. времени одного полного колебания.
При описании колебательного процесса часто необходимо знать закон изменения первой и второй производной. Допустим, интересующей нас динамической переменной является координата тела, изменяющаяся по гармоническому закону: x(t) = A cos(wt + j). Тогда первая производная - это проекция скорости на ось 0x, вторая производная – проекция ускорения:
vx =  =
= 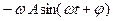 ; аx =
; аx =  =
=  = - w2x, (2)
= - w2x, (2)
где: v0 = wА - это амплитуда скорости; а0 = w2А – амплитуда ускорения.
Пример
Шарик массой m = 100 г, прикрепленный к достаточно жесткой пружине, совершает свободные гармонические колебания вдоль оси 0x с частотой n = 16 Гц. Амплитуда колебания координаты x равна 5 мм, начальная фаза колебаний j = 450. Записать уравнения колебаний в системе СИ для координаты x(t), проекции скорости vx(t), проекции ускорения ax(t) , проекции импульса px(t) через функцию косинуса. Определить законы изменения кинетической энергии шарика Eк(t), потенциальной энергии упругодеформированной пружины U(t) и полной механической энергии этого осциллятора.
Решение.
1.Колебание осциллятора совершается вдоль оси 0X. Запишем уравнение колебания координаты x через функцию косинуса:
x(t) = A cos(wt + j), (1)
тогда уравнение для проекции скорости примет вид:
vx = - w A sin(wt + j) = w A cos(wt + j + 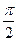 ), (2)
), (2)
Уравнение проекции ускорения аx = - w2A cos(wt + j) = w2A cos(wt + j + p). (3)
Т.к. px = mvx, то закон колебания проекции импульса имеет вид:
px = mwA cos(wt + j + 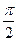 ), (4)
), (4)
где px0 = mwA – амплитуда импульса. Обратите внимание, колебания скорости (2) и импульса (4) опережают по фазе колебания координаты (1) на p/2 радиан (на 900), а ускорение (3) находится в противофазе с координатой (разность фаз p радиан или 1800).
Имеем: w = 2pn = 6,28×16 =100 (с-1); j = 450 = p/4 рад. (или j = 0,785 рад.);
v0 = wА =100×5×10-3 = 0,5 (м/с); px0 = mwA = 10-1×100×5×10-3 = 5×10-2 (кг×м/с);
аx0 = w2A = 1002×5×10-3 = 50 (м/с2).
Уравнения примут вид:
x(t) =5×10-3 cos(100t + p/4); vx = 0,5 cos(100t + 3p/4); аx = 50 cos(100t + 5p/4);
px = 5×10-2 cos (100t + 3p/4).
Видно, что разные динамические переменные одного и того же осциллятора совершают колебания со сдвигом фаз по отношению друг к другу.
Закон изменения кинетической энергии:
Eк(t) =  =
= 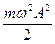 sin2(wt + j) =
sin2(wt + j) = 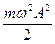 [
[  -
-  cos (2wt + 2j)], (5)
cos (2wt + 2j)], (5)
где Eк, max = 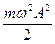 - максимальное значение кинетической энергии шарика. Закон потенциальной энергии: U(t) =
- максимальное значение кинетической энергии шарика. Закон потенциальной энергии: U(t) =  =
= 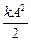 cos2(wt + j) =
cos2(wt + j) = 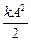 [
[  +
+  cos (2wt + 2j)], (6)
cos (2wt + 2j)], (6)
где Umax =  - максимальное значение потенциальной энергии пружины.
- максимальное значение потенциальной энергии пружины.
Кинетическая и потенциальная энергии изменяются с частотой 2w, т.е. в два раза превышающей частоту колебаний координаты. Из сравнения (5) и (6) следует, что кинетическая и потенциальная энергия изменяются в противофазе: когда потенциальная энергия достигает максимума, кинетическая энергия равна нулю и наоборот. При свободных гармонических колебаниях собственная частота осциллятора w2 =  , следовательно
, следовательно 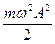 =
=  . Полная механическая энергия не изменяется в процессе колебаний: W = Eк(t) + U(t) =
. Полная механическая энергия не изменяется в процессе колебаний: W = Eк(t) + U(t) =  =
= 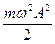 .
.
1.1.2. Методы (способы) представления колебаний
Колебательный процесс можно представить аналитически, временной диаграммой, спектральной диаграммой, векторной диаграммой, фазовой траекторией (диаграммой состояния).
а. Аналитически гармонические колебания выражаются уравнением колебаний с использованием тригонометрических функций синуса или косинуса. Например:
x(t) = A cos(wt + j).
В соответствии с формулой Эйлера  = cosj + i sinj (i =
= cosj + i sinj (i =  ) гармонические колебания аналитически можно представить и в комплексной форме. Под гармонической функцией в комплексном пространстве следует понимать экспоненту с мнимым показателем: x(t) = A
) гармонические колебания аналитически можно представить и в комплексной форме. Под гармонической функцией в комплексном пространстве следует понимать экспоненту с мнимым показателем: x(t) = A 
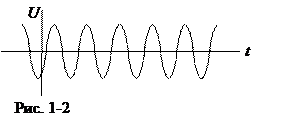 б. Гармонические колебания, например, напряжения в колебательном контуре U(t) = U0 cos(wt + j), можно представить графически временной диаграммой, т.е. графиком U(t), где по горизонтальной оси отложено время t, по вертикальной оси колеблющаяся динамическая переменная U (рис. 1-2). Эта диаграмма может быть получена с помощью осциллографа, подключенного, например, к активному сопротивлению колебательного контура.
б. Гармонические колебания, например, напряжения в колебательном контуре U(t) = U0 cos(wt + j), можно представить графически временной диаграммой, т.е. графиком U(t), где по горизонтальной оси отложено время t, по вертикальной оси колеблющаяся динамическая переменная U (рис. 1-2). Эта диаграмма может быть получена с помощью осциллографа, подключенного, например, к активному сопротивлению колебательного контура.
в.Если фазовые характеристики (фазовые соотношения) не интересны, то колебание удобно представлять графически спектральной диаграммой. На графике по горизонтальной оси откладывается частота w (или n =  ), а по вертикали амплитуда динамической переменной (или энергия, пропорциональная квадрату амплитуды и частоты). В случае гармонического колебания x(t) = A cos(wt + j) спектр состоит из одной частоты w (рис. 1-3а). В реальной колебательной системе в ее спектре содержатся набор частот в определенном частотном диапазоне (рис.1-3б).
), а по вертикали амплитуда динамической переменной (или энергия, пропорциональная квадрату амплитуды и частоты). В случае гармонического колебания x(t) = A cos(wt + j) спектр состоит из одной частоты w (рис. 1-3а). В реальной колебательной системе в ее спектре содержатся набор частот в определенном частотном диапазоне (рис.1-3б).

 г. Гармонические колебания можно представить векторной диаграммой. Гармоническое колебание x(t) = A cos(wt + j) определено, если заданы амплитуда А, начальная фаза j и циклическая частота w. Эти характеристики на векторной диаграмме выражаются следующим образом. Выбирается полюс 0 и луч ОМ (рис.1-4). Относительно луча ОМ отсчитывается начальная фаза. Из полюса проводится вектор А, модуль которого ра
г. Гармонические колебания можно представить векторной диаграммой. Гармоническое колебание x(t) = A cos(wt + j) определено, если заданы амплитуда А, начальная фаза j и циклическая частота w. Эти характеристики на векторной диаграмме выражаются следующим образом. Выбирается полюс 0 и луч ОМ (рис.1-4). Относительно луча ОМ отсчитывается начальная фаза. Из полюса проводится вектор А, модуль которого ра  вен амплитуде колебания, причем вектор Аповорачивается на угол j, равный начальной фазе колебания (положительный угол соответствует повороту против часовой стрелки, отрицательный – против). Мысленно считается, что вектор Авращается относительно полюса 0 с угловой скоростью w. Таким образом, векторная диаграмма отображает все характеристики уравнения колебаний.
вен амплитуде колебания, причем вектор Аповорачивается на угол j, равный начальной фазе колебания (положительный угол соответствует повороту против часовой стрелки, отрицательный – против). Мысленно считается, что вектор Авращается относительно полюса 0 с угловой скоростью w. Таким образом, векторная диаграмма отображает все характеристики уравнения колебаний.
д.Представление колебательного процесса с помощью фазовой траектории (диаграммы состояния). Этот способ рассмотрим на примере механической колебательной системы. Известно, что состояние и изменение состояния любой классической механической системы материальных точек с их известными массами полностью определено, если в данный момент времени одновременно заданы координаты и скорости всех материальных точек механической системы (в теоретическом курсе классической механики состояние системы задается координатами и импульсом). Пусть смещение материальной точки, прикрепленной к пружине, совершается по закону x(t) = A cos(wt + j), тогда скорость материальной точки изменяется по закону vx = 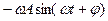 . Возведя в квадрат эти уравнения и принимая во внимание тождество cos2 (wt + j) + sin2 (wt + j) = 1, получим:
. Возведя в квадрат эти уравнения и принимая во внимание тождество cos2 (wt + j) + sin2 (wt + j) = 1, получим:
 +
+ 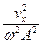 = 1 или x2 +
= 1 или x2 + 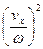 = A2.
= A2.
 Последнее уравнение - это уравнение окружности радиуса А (рис.1-5). Изображающая точка, т.е. точка на графике, изображающая состояние колебательной системы, движется равномерно по окружности по часовой стрелке.
Последнее уравнение - это уравнение окружности радиуса А (рис.1-5). Изображающая точка, т.е. точка на графике, изображающая состояние колебательной системы, движется равномерно по окружности по часовой стрелке.
Изображающая точка при движении образует фазовую траекторию. Если колебание гармоническое, то фазовая траектория представляет собой замкнутую кривую.
Фазовая траектория затухающих колебаний имеет вид спирали, скручивающейся к началу 0 (рис.1-6). Действительно, уравнение для смещения затухающих колебаний имеет вид:
x(t) = A 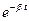 cos wt
cos wt
(для простоты за начальную фазу принято значение j = 0).
Уравнение скорости vx = 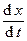 = - A
= - A 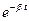 (b cos wt + w sin wt). При малых затуханиях (b<<w) vx = -Aw
(b cos wt + w sin wt). При малых затуханиях (b<<w) vx = -Aw 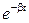 sin wt. Возведя в квадрат уравнения для смещения и скорости, получим:
sin wt. Возведя в квадрат уравнения для смещения и скорости, получим:
x2 +  = A2
= A2 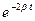 .
.
Это и есть уравнение спирали, скручивающейся к началу 0.
1.1.3. Динамика гармонического осциллятора
Пусть пружинный маятник совершает колебания малой амплитуды около положения устойчивого равновесия под действием возвращающей силы упругости, обусловленной деформацией пружины х (рис.1-7). При малых деформациях закон силы упругости подчиняется линейному закону Гука Fx = - kx. В отсутствии трения движение описывается линейным дифференциальным уравнением m  = - kx (второй закон Ньютона). Это уравнение можно записать в виде
= - kx (второй закон Ньютона). Это уравнение можно записать в виде  +
+  x = 0 .
x = 0 .
Отношение 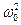 =
=  имеет размерность квадрата частоты и является собственной характеристикой пружинного маятника (т.к. определяется собственными свойствами колебательной системы: жесткостью пружины k и массой маятника m). Таким образом, уравнение можно зависать в видея:
имеет размерность квадрата частоты и является собственной характеристикой пружинного маятника (т.к. определяется собственными свойствами колебательной системы: жесткостью пружины k и массой маятника m). Таким образом, уравнение можно зависать в видея:
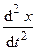 +
+ 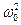 x = 0 или компактно
x = 0 или компактно 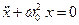 (3)
(3)
Решением уравнения (3) является гармоническая функция:
x(t) = A cos(w0t + j). (4)
Из решения видно, что, действительно, w0 = 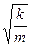 имеет смысл собственной циклической частоты. Период собственных колебаний T0 =
имеет смысл собственной циклической частоты. Период собственных колебаний T0 = 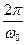 =
=  .
.

Пружинный маятник, совершающий гармонические колебания около положения равновесия под действием возвращающей силы вида Fx = - kx, является примером гармонического осциллятора. В конкретной колебательной системе возвращающая сила по своей природе не обязательно должна быть именно силой упругости.
Пример.
Описать свободные колебания ареометра массой m, помещенного в жидкость плотностью r. Площадь поперечного сечения горлышка ареометра равна S (см. рисунок к примеру). Вязким трением в жидкости пренебречь.
Решение
На ареометр массой действует сила тяжести и сила Архимеда. 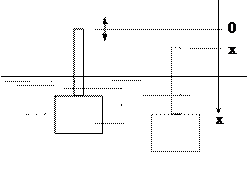 Если слегка притопить ареометр на глубину x, то сила Архимеда возрастет по модулю на величину F = rSxg . Понятно, что при всплытии ареометра выше положения равновесия сила тяжести будет на ту же величину F = rSxg больше силы Архимеда. Сила Архимеда направлена против направления смещения ареометра. Дополнительная сила Архимеда Fx = -rSxg играет роль возвращающей силы (напомним, в пружинном маятнике эту роль играет сила упругости). Второй закон Ньютона в проекции на ось 0Х имеет вид m
Если слегка притопить ареометр на глубину x, то сила Архимеда возрастет по модулю на величину F = rSxg . Понятно, что при всплытии ареометра выше положения равновесия сила тяжести будет на ту же величину F = rSxg больше силы Архимеда. Сила Архимеда направлена против направления смещения ареометра. Дополнительная сила Архимеда Fx = -rSxg играет роль возвращающей силы (напомним, в пружинном маятнике эту роль играет сила упругости). Второй закон Ньютона в проекции на ось 0Х имеет вид m  = - rSxg. После соответствующих преобразований дифференциальное уравнение примет вид:
= - rSxg. После соответствующих преобразований дифференциальное уравнение примет вид:  или
или  ,
,
где  - квадрат собственной частоты колебаний ареометра в жидкости. Решением уравнения является уравнение гармонических колебаний x = Xmax cos (w0t + j), Xmax – амплитуда колебаний ареометра.
- квадрат собственной частоты колебаний ареометра в жидкости. Решением уравнения является уравнение гармонических колебаний x = Xmax cos (w0t + j), Xmax – амплитуда колебаний ареометра.
Динамические уравнения колебаний пружинного маятника и ареометра и их решения имеют одинаковый вид. Роль возвращающей силы в пружинном маятнике играет сила упругости Fx = - kx. Для ареометра возвращающей силой является сила Архимеда, которая формально имеет тот же вид, что и сила упругости: Fx = -rSgx = - bx, где b = rSg. В этой связи возвращающая сила вида F = - bx получила название квазиупругойсилы, т.е. силы, формально схожей с упругой силой (приставка «квази» – от латинского quasi – якобы, как будто, вроде).
Приведем без детализации вывода динамические уравнения и собственные частоты двух других гармонических осцилляторов.

Рис.1-9
Математический маятник (рис. 1-8). Дифференциальное уравнение, описывающее динамику колебаний математического маятника, имеет вид:
J 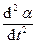 = - mgla,
= - mgla,
где J = ml 2 – момент инерции маятника относительно оси 0. Собственная частота маятника 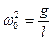 , период T =
, период T = 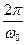 =
= 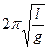 . Решение уравнения:
. Решение уравнения:
a = amax cos (w0t + j).
Колебания материальной точки m, прикрепленной к двум струнам (рис. 1-9). Дифференциальное уравнение имеет вид: m  = -
= -  . Собственная частота системы
. Собственная частота системы  , период T0 =
, период T0 = 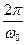 =
=  .
.
Решение уравнения: x = Xmax cos (w0t + j).
Полезно самостоятельно получить приведенные дифференциальные уравнения и решение этих уравнений.
В некоторых случаях динамику осциллятора удобно описывать не на языке сил, а энергий. Так поступают, например, при описании динамики квантовых осцилляторов с опосредованным использованием понятия квазиупругой силы. Действительно, в положении равновесия потенциальная энергия осциллятора U(x) имеет минимум. При малых колебаниях, т.е. малых амплитудах А, потенциальная энергия гармонического осциллятора имеет вид U(x) = 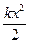 , тогда для малых колебаний квазиупругая сила примет вид:
, тогда для малых колебаний квазиупругая сила примет вид:
F = 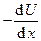 = - kx.
= - kx.
В квантовых системах динамику линейного квантового осциллятора решают с помощью уравнения Шредингера, где динамической переменной является не сила, а энергия. Потенциальная энергия осциллятора имеет тот же вид, что и в классическом осцилляторе, т.е. U(x) = 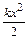 . При этом оказывается, что решение уравнения Шредингера существует лишь при дискретных значениях полной энергии квантового осциллятора.
. При этом оказывается, что решение уравнения Шредингера существует лишь при дискретных значениях полной энергии квантового осциллятора.
1.1.4. Динамика затухающих колебаний
Пусть пружинный маятник находится в вязкой среде (рис. 1-10). На материальную точку в этом случае действует сила сопротивления среды Fc = - mvx = - m 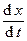 , где m - коэффициент сопротивления вязкой среды. 2-ой закон Ньютона в проекции на ось 0Х примет вид:
, где m - коэффициент сопротивления вязкой среды. 2-ой закон Ньютона в проекции на ось 0Х примет вид:  , или
, или  . Обозначим
. Обозначим 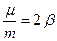 и учтем, что
и учтем, что  - квадрат собственной частоты колебательной системы. Тогда 2-ой закон Ньютона примет вид:
- квадрат собственной частоты колебательной системы. Тогда 2-ой закон Ньютона примет вид:
 . (5)
. (5)
Уравнение (5) - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
 |
Рис. 1-10
Решение дифференциального уравнения (5) ищется, как известно, с помощью подстановки экспоненциальной функции x(t) =  , где l = const, е - основание натурального логарифма. Напомним, функцию
, где l = const, е - основание натурального логарифма. Напомним, функцию  записывают также в форме exp (lt), т.е.
записывают также в форме exp (lt), т.е.  º exp (lt). Дважды продифференцируем x(t) =
º exp (lt). Дважды продифференцируем x(t) =  и результаты подставим в (5): l2 + 2 bl + w02 = 0.
и результаты подставим в (5): l2 + 2 bl + w02 = 0.
Полученное алгебраическое уравнение, соответствующее дифференциальному уравнению (5), называется характеристическим уравнением. Корнями этого уравнения являются: l1,2 = - b ±  . При малых затуханиях (при w0 >> b) подкоренное выражение будет отрицательным, следовательно, корень является мнимой величиной. Представим подкоренное выражение в виде (iw)2, где: i =
. При малых затуханиях (при w0 >> b) подкоренное выражение будет отрицательным, следовательно, корень является мнимой величиной. Представим подкоренное выражение в виде (iw)2, где: i =  - мнимая единица, w =
- мнимая единица, w =  - вещественная величина. Таким образом, решениями характеристического уравнения являются корни:
- вещественная величина. Таким образом, решениями характеристического уравнения являются корни:
l1 = - b + iw ; l2 = - b - iw ,
Условие w0 >> b означает, что сопротивление среды не слишком большое и колебательная система до полного затухания успевает многократно пройти через положение устойчивого равновесия. Корни характеристического уравнения l1 и l2 - это те значения l, при которых подстановка x(t) =  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению  . Решение дифференциального уравнения (5) при данных корнях характеристического уравнения l1 и l2 принимает вид:
. Решение дифференциального уравнения (5) при данных корнях характеристического уравнения l1 и l2 принимает вид:
x(t)= 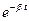 (C1
(C1  + C2
+ C2  ).
).
Функция x(t) описывает колебание, следовательно, эта функция должна быть вещественной. Условие вещественности означает равенство комплексно сопряженных величин:
C1  + C2
+ C2  = C1*
= C1*  + C2*
+ C2*  .
.
Следовательно, C1 = C2* и C2 = C1*. В показательной форме постоянные комплексные коэффициенты C1 и C2 можно представить, например, в виде: C1 = 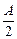
 ; C2 =
; C2 = 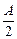
 . Подставим эти коэффициенты в решение (6):
. Подставим эти коэффициенты в решение (6):
x(t)= 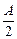 (
(  +
+  ). (6)
). (6)
Уравнение затухающих колебаний (6) можно представить в тригонометрической форме, воспользовавшись формулой Эйлера. Так как
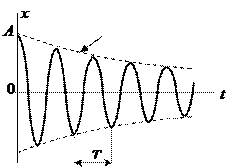
 = cosa + i sina ;
= cosa + i sina ;  = cosa - i sina, то cosa =
= cosa - i sina, то cosa =  (
(  +
+  ) и sina =
) и sina =  (
(  -
-  ), следовательно: x(t)=
), следовательно: x(t)= 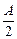 (
(  +
+  ) = A
) = A  cos (wt + a). (7)
cos (wt + a). (7)
График затухающих колебаний (7) приведен на рис. 1-11.
Рис. 1-11.
Частота затухающих колебаний определяется соотношением w = 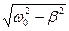 (частота затухающих колебаний w не равна собственной частоте w0 колебательной системы), период - T =
(частота затухающих колебаний w не равна собственной частоте w0 колебательной системы), период - T =  , где коэффициент b носит название коэффициента затухания. Приведенное решение верно при условии w0 > b. При w0>> b частота и период затухающих колебаний колебательной системы почти совпадают с собственной частотой и периодом этой колебательной системы: w » w0 и T »
, где коэффициент b носит название коэффициента затухания. Приведенное решение верно при условии w0 > b. При w0>> b частота и период затухающих колебаний колебательной системы почти совпадают с собственной частотой и периодом этой колебательной системы: w » w0 и T » 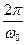 .
.
Проведем небольшой анализ решения (7).
Роль амплитуды в (7) играет величина A  , где А - амплитуда в момент времени t = 0. Амплитуда уменьшается по экспоненциальному закону (знак минус), следовательно, затухающие колебания не являются строго периодическими. Однако определенная периодичность проявляется, например, в повторяемости прохождения материальной точкой положения равновесия.
, где А - амплитуда в момент времени t = 0. Амплитуда уменьшается по экспоненциальному закону (знак минус), следовательно, затухающие колебания не являются строго периодическими. Однако определенная периодичность проявляется, например, в повторяемости прохождения материальной точкой положения равновесия.
Из выражения для переменной амплитуды затухающих колебаний A  определяется феноменологический смысл коэффициента затухания b. Показатель степени является всегда безразмерной величиной, следовательно, b в
определяется феноменологический смысл коэффициента затухания b. Показатель степени является всегда безразмерной величиной, следовательно, b в  измеряется в обратных секундах. Таким образом, коэффициент затухания может быть представлен в виде b =
измеряется в обратных секундах. Таким образом, коэффициент затухания может быть представлен в виде b = 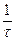 , где t - некоторое характерное время колебательной системы. За промежуток времени t = t амплитуда уменьшается в e » 2,7 раз (A
, где t - некоторое характерное время колебательной системы. За промежуток времени t = t амплитуда уменьшается в e » 2,7 раз (A  = A
= A 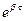 =
= 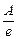 ). Итак, коэффициент затухания b равен обратной величине промежутка времени t, за которое амплитуда уменьшается в e » 2,7 раз. Заметим: уменьшение амплитуды в 2,7 раза (почти в 3 раза) на практике воспринимается как почти полное затухание колебаний. Время t часто называют временем релаксациизатухающих колебаний.
). Итак, коэффициент затухания b равен обратной величине промежутка времени t, за которое амплитуда уменьшается в e » 2,7 раз. Заметим: уменьшение амплитуды в 2,7 раза (почти в 3 раза) на практике воспринимается как почти полное затухание колебаний. Время t часто называют временем релаксациизатухающих колебаний.
Логарифм отношения значений амплитуд затухающих колебаний, отстоящих во времени на период называется логарифмическим декрементом затухания l:
l = ln 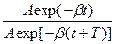 = ln
= ln 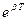 = bT.
= bT.
Само отношение амплитуд 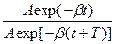 =
= 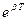 называется декрементом затухания.
называется декрементом затухания.
За время релаксации t колебательная система совершает Ne = 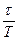 колебаний, где T – период колебания (время одного колебания). Из определения Ne следует, что Ne =
колебаний, где T – период колебания (время одного колебания). Из определения Ne следует, что Ne =  =
=  или l Ne = 1. Число Ne разных колебательных систем могут существенно различаться. Например, в обычных механических колебательных системах Ne может достигать нескольких десятков, в электрических контурах - нескольких сотен, у кварцевого резонатора может достигать значений Ne~106. Величина Ne определяет добротность колебательной системы Q, которая выражается формулой Q = =
или l Ne = 1. Число Ne разных колебательных систем могут существенно различаться. Например, в обычных механических колебательных системах Ne может достигать нескольких десятков, в электрических контурах - нескольких сотен, у кварцевого резонатора может достигать значений Ne~106. Величина Ne определяет добротность колебательной системы Q, которая выражается формулой Q = = 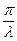 = p Ne, или Q »
= p Ne, или Q » 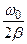 .Чем выше Ne, тем добротнее колебательная система.
.Чем выше Ne, тем добротнее колебательная система.
1.1.5. Динамика вынужденных колебаний. Импеданс колебательной
Системы
Вследствие потери энергии свободные колебания осциллятора являются затухающими. Для генерации незатухающих колебаний необходимо эти потери компенсировать. Например, затухание колебания качели можно компенсировать, если в нужный момент времени подталкивать качели. В этом примере внешняя вынуждающая сила является импульсной силой. Рассмотрим вынужденные колебания пружинного маятника под действием непрерывной гармонической вынуждающей силы Fx(t) = F0 coswt, где w - частота внешней вынуждающей силы (рис. 1-12).
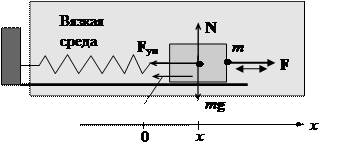 |
На колеблющееся тело маятника действуют сила сопротивления среды Fc = -m vx = - m 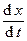 (примером является сила Стокса F = 6phRv) и сила упругости пружины Fуп. = - kx. Второй закон Ньютона примет вид:
(примером является сила Стокса F = 6phRv) и сила упругости пружины Fуп. = - kx. Второй закон Ньютона примет вид: 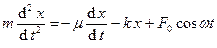 , или в компактной записи
, или в компактной записи
 , (6)
, (6)
где 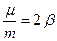 ;
;  . Уравнение (6) является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами 1, 2b,
. Уравнение (6) является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами 1, 2b, 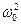 и
и  .
.
Известно, что решение неоднородного уравнения равно сумме общего решения однородного уравнения (т.е. уравнения 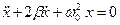 ) и частного решения неоднородного уравнения. Общее решение уравнения
) и частного решения неоднородного уравнения. Общее решение уравнения 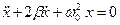 нами найдено в предыдущем параграфе. С течением времени затухающий член в решении неоднородного уравнения не вносит вклад в характер колебания материальной точки. Установившаяся часть вынужденных колебаний определяется частным решением неоднородного уравнения.
нами найдено в предыдущем параграфе. С течением времени затухающий член в решении неоднородного уравнения не вносит вклад в характер колебания материальной точки. Установившаяся часть вынужденных колебаний определяется частным решением неоднородного уравнения.
В теории дифференциальных уравнений рассматривается прием нахождения частного решения линейного неоднородного уравнения с постоянными вещественными коэффициентами. Этот прием заключается в том, что вначале находится решение соответствующего неоднородного дифференциального уравнения от комплексной функции, и, далее, из этого решения выделяется действительная часть, которая и будет решением исходного дифференциального уравнения. Остановимся на этом приеме.
Имеется некоторое неоднородное дифференциальное уравнение: 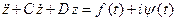 . Здесь С, D - вещественные постоянные коэффициенты; f(t) и y(t) - вещественные функции;
. Здесь С, D - вещественные постоянные коэффициенты; f(t) и y(t) - вещественные функции;  - мнимая единица. Функция z(t) является комплексной: z(t) = x(t) + iy(t), где x(t) и y(t) - вещественные функции. Комплексной функцией является и правая часть уравнения
- мнимая единица. Функция z(t) является комплексной: z(t) = x(t) + iy(t), где x(t) и y(t) - вещественные функции. Комплексной функцией является и правая часть уравнения 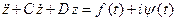 . После подстановки в это уравнение функцию z(t) = x (t) + iy (t)получим:
. После подстановки в это уравнение функцию z(t) = x (t) + iy (t)получим:
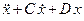 + i(
+ i(  ) =
) =  .
.
Так как два комплексных числа равны, если равны по отдельности их действительная и мнимая части, то:
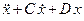 = f (t) и
= f (t) и  =
=  .
.
Из приведенных соотношений следует суть рассматриваемого приема для нахождения частного решения неоднородного дифференциального уравнения:
1) к правой части решаемого уравнения 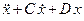 = f(t) прибавляется мнимая функция
= f(t) прибавляется мнимая функция  . При этом получается уравнение в комплексной форме
. При этом получается уравнение в комплексной форме 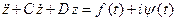 . Решением уравнения является комплексная функция z(t) = x (t) + iy (t);
. Решением уравнения является комплексная функция z(t) = x (t) + iy (t);
2) Из этого решения выделяется действительная часть x(t), которая и является решением уравнения 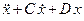 = f(t). Выбор функции
= f(t). Выбор функции 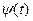 диктуется видом функции f(t) в соответствии с формулой Эйлера: если f(t) - функция косинуса, то в качестве
диктуется видом функции f(t) в соответствии с формулой Эйлера: если f(t) - функция косинуса, то в качестве 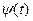 принимается функция синуса.
принимается функция синуса.
Перейдем к нахождению частного решения дифференциального уравнения (6). Прибавим к правой части (6) мнимую функцию (i  ), получим:
), получим:

 (где
(где  и
и 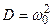 ) или по формуле Эйлера
) или по формуле Эйлера

 . (7)
. (7)
Искомой комплексной функцией является z(t) = x (t) + iy (t). В качестве решения выберем функцию z(t) = А  , где А - комплексная амплитуда. Определим А, для чего подставим z(t) в уравнение (7):
, где А - комплексная амплитуда. Определим А, для чего подставим z(t) в уравнение (7):
[ - w2A + i2bwA + 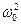 A]
A]  =
= 
 .
.
Т.к. данное уравнение выполняется при всех t, то А =


