Фазовая скорость волны

2015-12-15

1668

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Волновое уравнение. Волна на струне является поперечной волной: смещение частиц струны происходит поперек направления распространения волны. Это показано на рис. 1-24а. Волна распространяется в направлении оси 0x со скоростью с, смещение частиц струны происходит в направлении оси 0y со скоростью смещения частиц v_y.

Рассмотрим динамику движения элемента колеблющейся струны длиной dl при малых амплитудах колебаний элемента струны(малых колебаниях). На рис. 1-24б элемент dl представлен в крупном масштабе. Длина элемента определяется теоремой Пифагора:

dl = . (23)

Величина = tga, но при малых колебаниях угол a представляет малую величину, поэтому в (23) можно пренебречь ее квадратом. Таким образом, при малых колебаниях можно принять соотношение: dl = dx.

Выделенный элемент струны длиной dl и массой dm перемещается в направлении оси 0y (волна поперечная). Ускорение элемента a_y = . Если проекция результирующей силы натяжения в направлении оси 0y равна F_y, то 2-й закон Ньютона для выделенного элемента имеет вид: dm a_y = F_y.

Выразим массу элемента через линейную (погонную) плотность r материала струны: dm = r dl = r dx.

На струну действует сила натяжения F. Эта сила при малых колебаниях практически постоянна по модулю по всей длине струны. Мы не будем учитывать незначительные изменения силы натяжения вследствие разной степени растяжения струны в разных ее точках. Итак, составляющая результирующей силы F_y в положительном направлении оси 0y равна:

F_y = F sin(a + da) - F sina.

Угол a мал, поэтому sina = tga = , поэтому можно записать

F_y = F 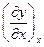- F = F .

Индексы при производных указывают, в каких точках эти производные берутся. Разность в квадратных скобках есть приращение производной на длине dx: = = .

Итак, сила, действующая на элемент струны в направлении оси 0y, равна

F_y = F .

Второй закон Ньютона dm a_y = F_y для элемента струны примет вид:

r dx = F или = .

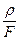
Отношение 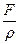имеет размерность квадрата скорости. Обозначим эту скорость через c, тогда последнее уравнение примет вид:

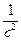
= . (24)

Уравнение (24) и есть волновое уравнение, описывающее распространение бегущей волны в струне, где

c = (25)

есть фазовая скорость распространения волны (рис. 1-25).

Обратим внимание на то, что фазовая скорость является функцией натяжения T и инертных характеристик струны - плотности r. Такая зависимость фазовой скорости присуща всем упругим волна – волнам в газе, жидкости, твердом теле. Например, скорость продольных акустических волн в тонких металлических стержнях определяется формулой: c = , где: E – модуль Юнга металла, характеризующий напряжение в стержне при единичной относительной деформации; r - объемная плотность металла. Скорость звука в газе определяется формулой: c = 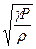, где g - показатель адиабаты газа, P – давление в газе, r - плотность газа. Во всех приведенных примерах фазовая скорость определяется упругими и инертными свойствами среды.

Решение волнового уравнения. Решение дифференциального волнового уравнения называют уравнением волны. Решением волнового уравнения (24) является любая функция вида y = f(ct – x) или y = f(ct + x) [убедитесь в этом, подставив, например, функцию f(ct – x) в (24)]. Знак минус соответствует волне, бегущей в положительном направлении оси 0x, знак плюс – в отрицательном направлении. Если генератор, возбуждающий волну, совершает гармонические колебания, то в качестве решения следует, естественно, выбрать функцию синуса или косинуса. Выберем, например, функцию синуса, тогда уравнение бегущей волны примет вид:

y = а sin [ (ct – x) +j ]. (26)

С формальной точки зрения множитель вставлен в решение (26) для того, чтобы аргумент синуса имел размерность угла. В содержательном отношении величина l - это длина волны, k = - волновое число, а – амплитуда волны, j - начальная фаза волны.

Из произведения x следует смысл l. При x = l фаза волны сдвигается на 2p радиан, следовательно, длина волны l – это минимальное расстояние между двумя частицами струны, которые колеблются в фазе. Из соотношения = w = следует, что фазовая скорость равна c = . Фазовая скорость c определяет скорость распространения некоторой фазы волны (рис. 1-25).

Так как = kc = w, x = kx и с = 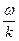, то уравнение бегущей волны (26) можно записать в виде

y = а sin (wt - kx+j ) (26^*)

или в виде y = а sin [w (t - 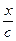) +j ]. (26^**)

Обратим внимание на то обстоятельство, что в составляющих аргумента уравнения бегущей волны отражены как пространственный (kx), так и временной (wt) аргументы волнового процесса. Если фиксировать координату x, то уравнение волны описывает гармонические колебание элемента (частицы) струны в точке с этой координатой. Если фиксировать время t, то уравнение волны описывает пространственные смещения частиц струны по всей ее длине в этот момент времени (струна имеет форму синусоиды). Оба аргумента – пространственный (kx) и временной (wt) – совместно описывают бегущую волну в пространстве и времени. Циклическая частота w = определяет сдвиг фазы в волне за единицу времени, волновое число k = определяет сдвиг фазы при перемещении волны на единицу длины.

Запишем уравнение плоской упругой волны в среде при произвольном направлении относительно системы отсчета. Допустим, плоская акустическая волна распространяется в упругой среде в направлении единичного вектора n относительно выбранной декартовой системы координат (рис. 1-26). В качестве начальной волновой поверхности выберем поверхность, проходящую через начало координат (на рисунке – это поверхность А). Колебания некоторой характеристики акустического поля h на начальной поверхности определится уравнением h_А = а sin (wt + j ).Через время t волновая поверхность сместится на расстояние l. Колебания h в любой точке этой новой поверхности, 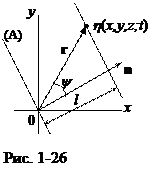определяемой радиус-вектором r, запишется в виде:

h = а sin (wt - kl + j ).

Скалярное произведение nr = r cos y = l, следовательно

h = а sin (wt - knr+ j ).

Вектор k =knназывается волновым вектором, модуль которого равен волновому числу, и направленный перпендикулярно волновой поверхности. Таким образом, уравнение волны при произвольном направлении ее распространения запишется в виде:

h = а sin (wt - kr+j ). (27)

Скалярноепроизведение kr = k_xx + k_yy + k_zz. Проекции волнового вектора можно представить через направляющие косинусы:

k_x = cosa, k_y = cosb, k_y = cosg,

где a, b, g - углы между волновым векторомk =kn и осями координат.

1.2.2. Стоячие волны на струне

Стоячая волна формируется в результате интерференции многократно отраженных бегущих волн от точек закрепления струны.

Предварительно определим характер изменения фазы бегущей волны в процессе двух последовательных отражений. На рис. 1-27 стрелками показаны направления движения падающих и отраженных бегущих волн. Бегущая волна «1» падает на правую точку закрепления струны «B», отраженная волна «2» падает на левую точку закрепления «A» , и после отражения волна «3» движется к правому закреплению. Пренебрежем затуханием волны в струне и потерями энергии волны при отражении. Отсутствие затухания означает, что амплитуда бегущей волны в процессе распространения по струне остается постоянной. Отсутствие потери энергии при отражении означает, что амплитуды падающей и отраженной волн в точке отражения одинаковы.

Бегущая волна «1», перемещающаяся в положительном направлении оси 0x, описывается уравнением волны:

y₁ = a₁ sin (wt - kx +j₁).

Отраженная бегущая волна «2», перемещающаяся в отрицательном направлении оси 0x, имеет вид:

y₂ = a₂ sin (wt + kx + j ₂),

Определим соотношение между начальными фазами j₁и j₂. В точке закрепления струны «B» (x = 0) колебания струны отсутствует:

y₁ + y₂ = a₁ sin (wt + j ₁) + a₂ sin (wt + j ₂) = 0.

Это уравнение справедливо при выполнении двух условий:

a₁ = a₂ и j₂= j ₁+ p .

Условие a₁ = a₂ означает, что отсутствуют потери энергии волны при отражении. Условие j₂= j ₁+ p указывает, что отраженная волна сдвинута по фазе от падающей волны на p радиан. Итак, уравнение бегущей волны «2» имеет вид: y₂ = a₂ sin (wt + kx + j ₁+ p).

Волна «2» отражается от опоры «B». Отраженная волна «3», которая перемещается в положительном направлении оси 0x, имеет вид:

y₃ = a₃ sin (wt - kx + j ₃).

Определим соотношение между начальными фазами j₁и j_3. Вточке крепления струны «A» колебание струны отсутствует:

y₂ + y₃ = a₂ sin (wt + kx + j ₁+ p) + a₃ sin [(wt - kx + j ₃] = 0.

Точка закрепления «A» имеет координату x = -L, и уравнение y₂ + y₃ = 0

справедливо при выполнении двух условий:

a₂ = a₃ и - k(-L) + j ₃= [k(-L) + j ₁+ p)] + p .

Из второго условия получим: j ₃= j ₁ - 2kL + 2p.

Учитывая соотношение k = , и отбрасывая полный угол 2p радиан, получим: j ₃= j ₁ - 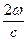L . Уравнение волны «3» принимает вид:

y₃ = a₃ sin [(wt - kx + j ₁ - 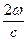L].

Волны «1» и «3» движутся в одну сторону. Результат сложения этих волн зависит от разности фаз между этими волнами. Итак, разность фаз волн «1» и «3» равна 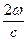L. Если разность фаз равна целому числу полного угла 2p, т.е. если 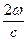L = n2p (n = 1, 2, …), (28)

то волны «1» и «3» находятся в фазе, и их амплитуды складываются – наблюдается максимум интерференции этих волн. В противном случае волны будут гасить друг друга. Подставляя связь между круговой частотой и длиной волны w = в соотношение (28), получим:

L = n . (28^*)

Синфазное распространение волн «1» и «3» реализуется, если на длине струны укладывается целое число полуволн.

Аналогичный результат получится и для волн, бегущих справа налево - от опоры B к опоре A. При этом волны, бегущие от B к A, находятся в противофазе с волнами, бегущими от A к B за счет сдвига фазы на p радиан при отражении от опоры.

Если условие (28^*) не выполняются, то при многократном отражении разность их фаз непрерывно изменяется, что приводит к уменьшению результирующей амплитуды, волны начинают гасить друг друга.

В реальном эксперименте потери энергии при отражении неизбежны, неизбежно также и затухание волны при распространении по струне. Часть энергии волны передается устройствам крепления струны - опорам, а часть переходит во внутреннюю энергию материала струны, в результате чего струна нагревается. Поэтому полученное равенство амплитуд бегущих волн a₁= a₂ = … = a_m = ... не выполняется – амплитуды a_m уменьшаются. Вследствие потерь энергии сдвиг фазы на p радиан при отражении также точно не выполняется, ибо в точках крепления струны наблюдаются незначительные колебания, обеспечивающие передачу энергии креплению струны.

Уравнение стоячей волны. Результирующее колебание струны обусловлено интерференцией встречных волн. Обозначим результирующую амплитуду волн [при выполнении условия (28^*)], бегущих в положительном направлении оси 0x, через Y₍_®₎, а в обратном направлении – через Y₍₎. Здесь: Y₍_®₎= a₁+ a₃ + a₅ + … ; Y₍₎= a₂+ a₄ + a₆ + … Вследствие потерь энергии результирующие амплитуды Y₍_®₎и Y₍₎имеют конечное значение и не равны друг другу. Уравнение результирующей волны, бегущей в положительном направлении оси 0x, имеет вид:

y₍_®) = Y₍_®)sin (wt – kx).

Уравнение результирующей волны, бегущей в отрицательном направлении оси 0x, имеет вид:

y₍₎= Y₍₎sin (wt + kx + p) = - Y₍₎sin (wt + kx).

Результирующая волна на струне определится суммой встречных бегущих волн: y = y₍_®) + y₍₎ = Y₍_®)sin (wt – kx) - Y₍₎sin (wt + kx).

Прибавим и вычтем вспомогательную величину[Y₍_®)×sin (wt + kx)], получим:

y =[Y₍_®₎sin (wt – kx) – Y₍_®₎sin (wt + kx)] + [Y₍_®₎sin (wt + kx) - Y₍₎sin (wt + kx)],

или

y =-2Y₍_®₎sin kx ×cos wt + (Y₍_®₎ - Y₍₎)×sin(wt + kx). (29)

Уравнение (29) описывает волновой процесс в струне.

Проведем анализ уравнения.

1. При Y₍_®) = Y₍₎ в уравнении (29) остается первый член, который описывает стоячую волну: y =-2Y₍_®)sin kx ×cos wt. Второй член в (29) равен нулю. Амплитуда колебаний частиц струны 2Y₍_®)sinkx определяется координатой этих частиц. В точках с координатами, отвечающими условию sin kx = 0, т.е. условию kx = np, колебания отсутствуют. Эти точки на струне называются узлами стоячей волны. Координаты узлов: т.к. k = , то

x_узел = n , n = 1, 2, 3, …

В частности, в точках крепления (x = 0 и х =L) находятся узлы стоячей волны. Имеем L = n , т.е. при реализации на струне стоячей волны, на струне укладывается целое число полуволн. Полученное соотношение коррелирует с формулой (28^*). При заданной длине струны L определим набор собственных частот струны n_n , при которых формируется стоячая волна: так как

L = n = n , то n_n = n 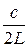, или n_n = n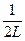 т.к. c = .

Частота n₁ (n = 1, т.е. на струне укладывается одна полуволна), называется основным тоном струны, остальные собственные частоты называются обертонами. Собственные частоты - основной тон и обертона - еще называют резонансными частотами.

Определим максимумы интерференции встречных волн. В точках струны, отвечающих условию ÷sin kxê = 1, имеем максимумы амплитуды колебания в стоячей волне. Эти максимумы называются пучностями стоячей волны. Так как kx =(2n + 1) 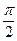, где n = 1, 2, …, то координаты пучностей определяются формулой x_пучн. = (2n + 1) .

График стоячей волны в отсутствии потерь приведен на рис. 1-28. Частицы струны между узлами колеблются в фазе. При переходе через узел фаза изменяется на p радиан (противофазные колебания частиц на соседних участках струны при переходе через узел).

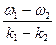
В стоячей волне энергия не переносится, в узлах колебания отсутствуют. Однако в отсутствии потерь нет и необходимости компенсировать потери. В реальном же эксперименте потери неизбежны, поэтому Y₍_®₎ ¹ Y₍₎, и бегущая волна вызывает небольшие колебания в узлах, вследствие чего узлы размываются.

1.2.3. Импеданс среды (на примере струны)

В § 1.1.7 выяснили, что феноменологический смысл механического импеданса колебательной системы определяется как внешняясила, которая необходима для сообщения колебательной системе единичную амплитудную скорость Z = 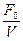. Определим импеданс струны как среды, в которой распространяется волна. Так как в струне распространяется поперечная волна, то этот импеданс естественно назвать поперечным импедансом. Подействуем на струну внешней гармонической силой F = F₀ 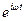в точке x = 0 в перпендикулярном направлении к струне. В этом случае уравнение бегущей волны имеет вид: y = a .

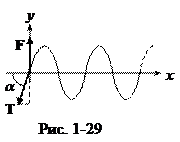Пусть натяжение струны T. В вертикальном направлении имеем:

F₀ 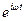» T tga = -T .

Так как = -ika 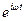, то F₀ 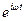= T ika 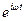. Из этого равенства получим значение амплитуды смещения: a = . Поперечная колебательная скорость v_y = 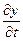= = 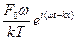. Так как , то в точке x = 0 скорость имеет вид: v_y = 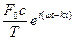= = V .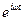

Следовательно, импеданс струны определяется выражением:

Z = = = .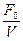

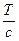Фазовая скорость волны связанас натяжение T и плотностью струны r соотношением c = , поэтому можно записать:

Z =rс. (30)

Отметим, импеданс среды еще называют волновым сопротивлением среды.

1.2.4. Отражение и прохождение волны на границе двух сред