ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

Законы электростатического и магнитостатического полей довольно подробно описаны в курсе общей физики. В первых двух главах кратко остановимся на содержании законов и уравнений, описывающих эти поля.

3.1.1. Объекты электростатики

Напомним объекты, которыми оперирует электростатика:

1) неподвижное точечное заряженное тело, обладающее электрическим зарядом q и инертной массой m. Единицей заряда в системе СИ служит кулон (Кл), 1Кл = 1А×1с. Подчеркнем, точечный заряд – это модельный объект электромагнетизма;

2) электрическое поле, порождаемое заряженным телом. Основной характеристикой поля является вектор напряженности электрического поля E. Напряженность электрического поля определяется силой, действующей со стороны поля на единичный заряд: 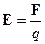. Из приведенной формулы следует, что единицей напряженности служит , однако единицу напряженности обычно выражают через работу электрического поля при перемещении единичного заряда на единичное расстояние в поле (вольт/метр): .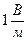

Заряды подчиняются закону сохранения заряда: в замкнутой системе алгебраическая сумма зарядов сохраняется. Вспомним, например, схему распада свободного нейтрона:

n ® p⁺ + e^- + .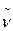

Приведенный распад иллюстрирует закон сохранения заряда. Действительно, нейтрон n электрически нейтральная частица, протон p⁺ положительно заряженная частица, электрон e^- отрицательно заряженная частица, антинейтрино 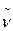электрически нейтральная частица. По модулю заряды протона и электрона равны. Кроме того, заряд инвариантен относительно выбора системы отсчета (следовательно, заряд не зависит от скорости движения заряженной частицы). Заряд системы до распада равен алгебраической сумме заряда системы после распада (в этом распаде - сумма равна нулю).

 

3.1.2. Закон Кулона. Напряженность электростатического поля и

интегральная теорема Гаусса

Закон Кулона. Экспериментальные исследования Кулона и Кавендиша показали, что взаимодействие зарядов подчиняется закону обратного квадрата. Закон взаимодействия двух точечных зарядов (закон Кулона) имеет вид:

F = . (1)

Попутно напомним, в опытах Кулона сила взаимодействия двух заряженных тел измерялась с помощью «крутильных весов». Опыты Кавендиша – пример применения «нулевого» метода в выявлении закона взаимодействия. Можно показать, что если закон электростатической силы является законом обратного квадрата, то в объеме заряженного проводника заряды должны отсутствовать – заряды будут находиться только на поверхности проводника. Этот эффект – отсутствие зарядов в объеме заряженного проводника – и был выявлен Кавендишем. Тем самым Кавендиш, независимо от Кулона, также пришел к закону обратного квадрата (1) – закону, носящий имя Кулона.

Взаимодействие зарядов осуществляется через электростатическое поле, создаваемое зарядами. Основной характеристикой поля является напряженность поля E. При помещении заряда q в полеE, на этот заряд со стороны поля действует сила

F = qE. (2)

Выражение для Eзаряженных тел разной формы имеет каждый свой вид. В частности, из сравнения (1) и (2) следует, что формула для расчета напряженности поля точечного заряда, например заряда q₁,имеет вид:

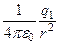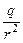
E₁ = илиE = 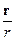. (3)

Cила, действующая на точечный заряд q₂, определится выражением:

F₂ = q₂E₁ = q₂ .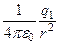

Напряженность поля вне заряженной сферы радиуса R (r ³ R) также выражается формулой (3). В объеме сферы поле отсутствует. Еще раз подчеркнем, отсутствие поля в объеме заряженной сферы является следствием закона обратного квадрата (1).

Пространственная конфигурация вектора E, т.е. направление вектора E и относительное изменение модуля E в пространстве, наглядно отображаются с помощью силовых линий. Вектор напряженности E направлен по касательной к своим силовым линиям, а изменение густоты силовых линий показывает относительное изменение модуля этих векторов (рис. 3-1). Способ отображения полей с помощью силовых линий будет использован при раскрытии содержания уравнений Максвелла.

Поток вектора через поверхность. Поток вектора через площадку зависит, естественно, от ориентации площадки относительно направления вектора. Если площадка перпендикулярна вектору, то поток максимален, если вектор направлен параллельно площадки, то вектор не пронизывает ее и поток вектора через такую площадку равен нулю. Для определения ориентации площадки вводится понятие вектора-площадки dS = ndS, где n– единичный безразмерный вектор, перпендикулярный элементарной площадке dS (рис. 3-2). Под элементарным потоком dФ вектора E через ориентированную элементарную площадку dS понимается скалярное произведение E на dS:

dФ = E dSº E dS cos α,

где угол α – угол между векторами Eи dS . Максимальный поток вектораE через площадку dS будет при α = 0⁰; нулевой поток – при α = 90⁰, в этом случае вектор E не пронизывает площадку dS.

 

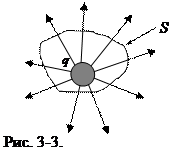
Теорема Гаусса. Поток вектора напряженности электростатического поля через замкнутую поверхность зависит только от заряда внутри полости, охватываемой поверхностью (рис. 3-3):

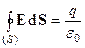или , (4)

где: q - алгебраическая сумма всех зарядов внутри полости; V – объем, охватываемый поверхностью S; r =r (x, y, z) – плотность заряда в объеме V. Теорема Гаусса является следствием закона Кулона как закона обратного квадрата (вывод теоремы можно найти в учебниках курса общей физики).

Если заряды находятся вне замкнутой поверхности, то поток E через эту поверхность равен нулю. Если в объеме V имеются заряды, но их алгебраическая сумма равна нулю, то и поток из полости равен нулю: . Таким образом, если даже поток вектора Eчерез замкнутую поверхность равен нулю, то это еще не означает, что в объеме замкнутой поверхности отсутствуют заряды.

 

 

 

Рассмотрим теорему Гаусса при наличии диэлектрика в объеме замкнутой поверхности. Диэлектрики – вещества, в которых концентрация свободных зарядов, которые могут участвовать в электрическом токе, незначительна. В диэлектрике заряженные частицы (валентные электроны или ионы) связаны со своими молекулами. Эти заряды так и называются – связанные заряды. При помещении диэлектрика во внешнее электрическое поле диэлектрик поляризуется. Электрическое полеE в диэлектрике определяется суперпозицией внешнего поля E₀ и макроскопического поля поляризованных зарядов E^/:

E=E₀ +E^/.

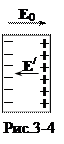Поляризация диэлектрика. Явление поляризация на микроуровне заключается в ориентации дипольных моментов молекул p = ql в направлении внешнего электрического поля E₀. В диэлектрике, состоящем из полярных молекул, их дипольные моменты ориентируются во внешнем поле и суммарный дипольный момент единицы объема становится не равным нулю. В неполярных молекулах собственный дипольный момент отсутствует. В диэлектриках из неполярных молекул дипольный момент p наводится внешним полем – положительные заряды молекулы смещаются в направлении внешнего поля, отрицательные против поля. Наведенный дипольный момент также ориентируется во внешнем поле. Таким образом, при помещении диэлектрика во внешнее электрическое поле, диэлектрик приобретает дипольный момент . Напомним также, что в объеме однородного диэлектрика связанные (поляризованные) заряды компенсируют друг друга. Нескомпенсированными остаются только заряды на поверхности диэлектрика (рис.3-4). Если диэлектрик неоднородный, то нескомпенсированные заряды возникают и в объеме диэлектрика.

Вектор поляризованности P и вектор смещения D. Суммарный дипольный момент диэлектрика во внешнем поле определяется двумя факторами: ориентирующим действием электрического поля в диэлектрикеEна дипольные моменты молекулp = ql и разориентацией дипольных моментов молекул вследствие их теплового хаотического движения. Степень поляризации диэлектрика естественно характеризовать поляризацией единицы объема диэлектрика - вектором поляризованности P:

P = .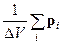

Из эксперимента следует, поляризованность во многих практически важных случаях пропорциональна напряженности электрического поля в диэлектрике:

P = ce₀E.

где c - диэлектрическая восприимчивость среды (c > 0).

Выделим в диэлектрике объем DV, охватываемый замкнутой поверхностью S. При поляризации диэлектрика дипольные моменты молекул поворачиваются в направлении поля. На границе S из объема DV наружу выдут части поляризованных молекул (заряженные или положительным, или отрицательным зарядом), и выделенный объем DV приобретает избыточный связанный заряд q^/.

Можно показать, что поток вектора поляризованности P через произвольную замкнутую поверхность S равен избыточному связанному заряду q^/ внутри поверхности, взятому с обратным знаком:

.

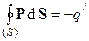Из приведенных выражений следует, что поляризованность P измеряется в единицах поверхностной плотности заряда - Кл/м².

 

В теореме Гаусса (4) под зарядами q понимаются все заряды – и свободные, и связанные (поляризованные) заряды: q = q_своб. + q^/. Имеем:

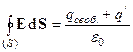, но ,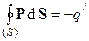

поэтому теорему Гаусса (4) можно записать в виде:

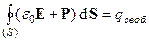. (5)

Введем вспомогательный вектор D = e₀E+ P= (1 +c)e₀E =ee₀E. Вектор D называют вектором смещения, где e = 1+c - диэлектрическая проницаемость среды. Запишем теорему Гаусса для вектора смещения:

или , (5^*)

где r_своб. – плотность свободных зарядов.

Подчеркнем, вектор смещенияD =ee₀Eзависит как от свободных зарядов q_своб., так и связанных зарядов q^/, что следует, например, из определения этого вектора D = e₀E+ P. Однако свойство этого вектора таково, что его поток определяется только свободными зарядами q_своб.. Во многих практически важных случаях вектор Dопределяется только свободными зарядами, именно в этих случаях векторD полезен при расчетах полей. Вектор D имеет ту же размерность, что и вектор поляризованности P, и измеряется в Кл/м².

Заметим также, что часто, исходя из смысла уравнений, индекс «своб.» при заряде опускают.

Применение теоремы Гаусса к расчету поля.

В тех случаях, когда силовые линии напряженности электрического поля равномерно распределены по поверхности заряженного тела, теорема Гаусса позволяет непосредственно рассчитать напряженность поля. Напомним, что число таких задач весьма ограничено. К этим задачам относятся: задача определения поля заряженной сферы, поля заряженной плоскости (конденсатора); поля заряженной нити (цилиндра).

1. Поле однородно заряженной сферы (рис. 3-5).

Пусть сфера радиуса R равномерно заряжена зарядом q. Окружим заряженную сферу мысленной концентрической сферой c радиусом r и площадью S^/ = 4pr². Вследствие симметрии задачи, напряженность поля E везде на поверхности S^/ одинакова и перпендикулярна к этой поверхности. По теореме Гаусса поток Eчерез замкнутую поверхность S^/ равен заряду внутри S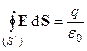^/: . Имеем:

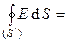E4pr², но E4pr² = 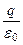. Итак: E = .

Из теоремы Гаусса следует, что в объеме заряженной сферы поле равно нулю. В объеме сферы заряды отсутствуют, следовательно, поток через мысленную замкнутую поверхность, проведенную внутри заряженной сферы, также равен нулю 0, поэтому E_{(внутри)}= 0.

2. Поле заряженной плоскости (рис. 3-6).

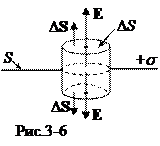Пусть бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда s = 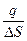. В качестве замкнутой поверхности выберем цилиндр, боковая поверхность которого перпендикулярна плоскости S, а торцевые поверхности имеют площадь DS. Поле Eперпендикулярно S и пронизывают только торцевые поверхности DS. По теореме Гаусса имеем:

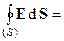2 EDS = .

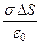Таким образом: E = . Поле является однородным и не зависит от расстояния до плоскости.

Полученное значение для заряженной плоскости позволяет определить поле в объеме конденсатора без учета краевых эффектов. Из рис.3-7 видно, что вне конденсатора поле равно нулю. В объеме конденсатора напряженность в два раза больше, чем напряженность заряженной плоскости с тем же значением поверхностной плотности заряда:

E = 2 = .

3. Поле заряженной нити (рис. 3-8). Пусть бесконечная нить заряжена с линейной плотностью заряда t = . В качестве замкнутой поверхности выберем цилиндр радиуса r и длиной l, осью которого является заряженная нить. Вследствие симметрии поля в радиальном направлении напряженность поля везде на боковой поверхности мысленного цилиндра одинакова по модулю. Вектор E не пронизывает торцевые поверхности цилиндра и везде перпендикулярен боковой поверхности цилиндра. Площадь боковой поверхности S_б = 2p r×l .

 

 

По теореме Гаусса 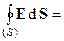E ×2p r×l = . Окончательно имеем:

E = .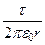

 

3.1.3. Дифференциальная форма теоремы Гаусса. Дивергенция

Электрического поля

Пусть в некоторой области пространства задана напряженность электростатического поля E(x,y,z). Требуется найти положение (координаты) и значение заряда q(x,y,z) в каждой точке пространства по заданному полю.

На первый взгляд представляется, что для решения задачи можно непосредственно использовать теорему Гаусса. Для этого просто следует стянуть замкнутую поверхность к рассматриваемой точке пространства с координатами (x,y,z), и затем вычислить поток вектора E(x,y,z) из бесконечно малого объема dV. Это должно, в соответствии с теоремой Гаусса, позволить определить значение заряда в бесконечно малом объеме.

Однако непосредственное применение теоремы Гаусса не приводит к решению задачи. Дело в том, что поток вектора через бесконечно малую замкнутую поверхность является также величиной бесконечно малой, причем третьего порядка малости.

 

Покажем это. Разложим вектор напряженности E(x,y,z)= E_xi + E_yj + E_kk в ряд Тейлора в рассматриваемой области с объемом dV, ограниченного бесконечно малой замкнутой поверхностью dS. Например, для компоненты E_x с учетом производной только первого порядка (остальные члены ряда имеют второй, третий и т.д. порядок малости) будем иметь:

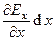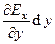E_x = E_x(0) + + + + … = E_x(0) + ,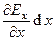

т.к. 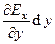= 0, = 0. Здесь член ряда E_x(0) – постоянная величина. Аналогичные выражения записываются для остальных компонент вектора E(x,y,z):

E_y = E_y(0) + ; E_z = E_z(0) + .

Все три разложения компонент можно совместно записать с использованием двух индексов (например, i и k). Запишем координаты (x,y,z) в виде (x₁,x₂ x₃), имеем:

E_i = E_i(0) + ,

где: i = 1, 2, 3; k = 1, 2, 3. При i ¹ k член суммы равен нулю.

Определим поток E(x,y,z) через бесконечно малую замкнутую поверхность dS: 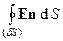= 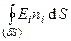, где: dS – элемент бесконечно малой замкнутой поверхности dS; единичный вектор n – нормаль к элементу поверхности dS. Имеем:

= = =

= + .

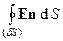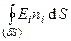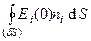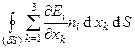Поток постоянного вектора через замкнутую поверхность равен нулю:

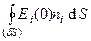=0.

Поток через бесконечно малую замкнутую поверхность dS (охватывающую бесконечно малый объем dV) определяется только выражением 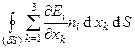. Видно, что этот объемный интеграл (произведение dxdS) является величиной третьего порядка малости. Что и требовалось показать.

 

Если взять отношение потока из бесконечно малого объема к этому объему (отношение потока как третьего порядка малости к объему также третьего порядка малости), то полученная величина будут конечной величиной и может служить величиной заряда в рассматриваемой точке пространства. Разделим теорему Гаусса (4) на объем, охватываемый поверхностью, и возьмем предел этого отношения при V ® 0:

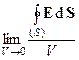= (6)

Здесь правый предел есть объемная плотность заряда в рассматриваемой точке: = .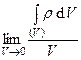

Следовательно, имеем: = .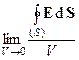

Левый предел в (6) называется дивергенцией (расхождением) вектора Eв рассматриваемой точке:

divE = 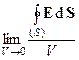. (7)

Итак: divE = . (8)

Уравнение (8) является дифференциальной формой теоремы Гаусса (4).

 

Теорема Гаусса-Остроградского. Исходя из определения дивергенции (7), получим важную интегральную теорему векторного анализа – теорему Гаусса-Остроградского.

Рассмотрим конечный объем V, ограниченный поверхностью с площадью S (рис.3-9). Разобьем этот объем на бесконечно малые параллелепипеды, площадь поверхности которых dS и объем dV.Из (7) следует, что бесконечно малый поток через dS из бесконечно малого объема параллелепипедов dV определяется выражением

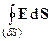= div E dV.

Просуммируем потоки от всех параллелепипедов, получим:

=

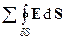Левая сумма в этом выражении является суммой потоков вектора E из бесконечно малых параллелепипедов. Нормали к смежным граням соседних бесконечно малых параллелепипедов направлены навстречу, поэтому соответствующие потоки компенсируются. Остаются некомпенсированными потоки через внешнюю поверхность S. Из этого следует, что левая сумма равна потоку E через внешнюю поверхность S рассматриваемого объема V:

= .

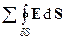Правая сумма есть объемный интеграл от дивергенции по всему рассматриваемому объему V:

= .

Итак, приходим к теореме Гаусса-Остроградского:

= . (9)

Теорема Гаусса-Остроградского (9) позволяет преобразовать объемный интеграл в поверхностный интеграл. Разумеется, функция E(x, y, z) должна быть конечной и непрерывной вместе со своими первыми производными во всех точках рассматриваемого объема V.

 

Теорема Гаусса-Остроградского также приводит к уравнению (8). Действительно, из сравнения (9) и теоремы Гаусса для вектора E (4) непосредственно следует уравнение (8):

divE = .

Сравнивая (9) с теоремой Гаусса для вектора D (5^*), получим дифференциальную форму этой теоремы:

div D = r_(своб.) (10)

Дивергенция инвариантна относительно преобразования координат. Относительно декартовой системы координат дивергенция вектораE имеет вид (вывод несложный, который можно найти в курсе общей физики):

divE = .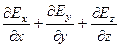

Теперь уравнение (8) можно записать в развернутом виде:

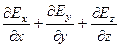= . (11)

Итак, заряды r в данной точке пространства порождают дивергенцию вектора E из данной точки.

Аналогичный развернутый вид имеет и уравнение (10):

= r_(своб.). (12)

Поставленная выше задача решается с помощью уравнений (11) и (12). Действительно, например, по заданным значениям компонент (E_x, E_y, E_z) можно рассчитать плотность зарядовr (x,y,z) в пространстве. В частности, если сумма производных =0, то это означает, что в рассматриваемой точке заряды отсутствуют ( =0).

 

Рассмотрим простой пример расчета распределения заряда по заданному полю вектора D. Допустим, вектор D направлен везде по радиус-вектору r, причем:

1) D = br при 0 £ r £ R ; 2) D = b rпри R £ r £ ¥,

где: r = xi + yj + zk; b – постоянный коэффициент; R – заданный радиус.

Для области пространства 0 £ r £ R имеем:

D_x = bx; D_y = by; D_z = bz.

Для области пространства R £ r £ ¥ имеем:

D_x = b x; D_y = b y; D_z = b z, где r³ =

Для области 0 £ r £ R

= b, поэтому в этой области divD = = 3b = const.

 

Для области R £ r £ ¥

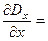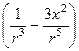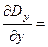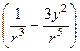bR³ ; bR³ ; bR³ .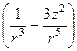

В этой области divD = = = 0.

Итак, в первой области 0 £ r £ R во всех точках содержится заряд с однородной плотностью заряда = 3b. В области R £ r £ ¥ заряды отсутствуют. Таким образом, первая область представляет собой однородно заряженный шар радиуса R.

 

Дивергенцию вектораE можно записать с помощью векторного оператора набла Ñ (оператора Гамильтона):

Ñ = + + .

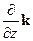Оператор Ñ рассматривается как вектор, точнее – символический вектор. Запишем скалярное произведение символического оператора набла Ñ = 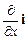+ + на вектор E =E_xi +E_yj + E_zk:

ÑE =( 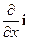+ + 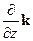) (E_xi +E_yj + E_zk)= .

Полученный результат есть divE. Итак, уравнение(8)можно записать в форме ÑE = , (13)

а уравнение (10) в форме ÑD = r_своб.. (14)

Заметим, выражение типа EÑ = (E_xi +E_yj + E_zk) ( 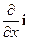+ + 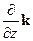) не является числом, а все еще остается некоторым оператором.

3.1.4. Работа электростатического поля. Потенциал

электростатического поля

Работа электростатического поля. Потенциал и разность потенциалов.Встречающиеся в практике законы сил обычно являются или функциями координат (радиус-вектора) F(r), или функциями относительной скорости F(v) взаимодействующих тел. «Экзотические» силы, зависящие от ускорения - силы вида F(а), в практике встречаются весьма редко. Примером силы видаF(а) является так называемое радиационное сопротивление. Примерами сил вида F(r) является гравитационная сила F = 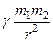, сила упругости F = - kx. Кулоновская сила F = также, разумеется, относится к силам вида F(r). К силам вида F(v), относятся, например, сила вязкого трения Стокса F = 6phRv, сила Лоренца F = qvB sina.

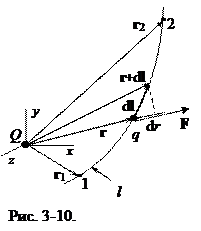Напомним, важной особенностью силовых полей вида F(r) является тот факт, что каждая точка такие поля обладают скалярной характеристикой - скалярным потенциалом j(x,y,z). В этой связи силовые поля вида F(r) называют потенциальными полями. Покажем, что работа стационарного (постоянного во времени) электростатического поля определяется начальным и конечным положениями перемещающегося тела, и не зависит от вида траектории тела.

Поместим заряд Q в начало системы отсчета, тогда электростатическое поле, создаваемого зарядом Q, в выбранной системе отсчета будет стационарным (рис.3-10). Вычислим работу электростатического поля, создаваемого зарядом Q, при перемещении заряда q в этом поле по траектории l из точки (1) в точку (2). По определению конечная работа

A = = ,

где a - угол между векторами Fи dl. Из рисунка видно, что (dl cosa) = dr. Величина dr – это бесконечно малое изменение расстояния между Q и q при перемещении заряда q по траектории на величину dl (перемещение dl– бесконечномалая величина). Итак, имеем:

A = = = 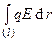= 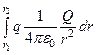q = q (j₁ - j₂). (15)

Итак, A = q (j₁ - j₂) = - q Dj . (15^*)

Напомним, символом D (дельта) принято обозначать приращение величины, т.е. разность между конечным и начальным значением величины:

Dj = (j₂ - j₁).

Величина (j₁ - j₂) = - Dj называется убылью величины j.

Элементарная порция работы поля dA на элементарном перемещении dl определяется бесконечно малым приращением потенциала:

dA = - q dj.

Как видно из (14), работа стационарного электростатического поля не зависит формы траектории (или, как говорят, не зависит от формы пути), а определяется начальным (r₁) и конечным (r₂) положениями заряда q. В частности, на замкнутой траектории при возвращении заряда q в начальное положение, работа поля равна нулю.

Определение. Стационарное потенциальное поле, работа которой не зависит от пути перехода из начального положения в конечное положение и определяется только этими начальным и конечным положениями, называется консервативным полем. Стационарное электростатическое поле является консервативным полем.

 

Замечание.

1. Не всякое потенциальное поле является консервативным. Например, работа поля, в которой проекции силы зависят от координат по закону F_x = ay; F_y = ax; F_z = 0 (а – положительная константа), на замкнутой траектории не равна нулю (проверьте).

2. Магнитная сила ЛоренцаF = q[v, B] является функцией скорости, поэтому магнитное поле не является потенциальным полем. Следовательно, у магнитного поля не существует скалярной характеристики – скалярного потенциала. Однако работа магнитной силы Лоренца равна нулю не только на замкнутой траектории, но и на любом участке движущегося заряда, т.к.вездеdl^B(ибо v^B). Вследствие равенства нулю работы силы Лоренца на замкнутой траектории, эту силу называют псевдоконсервативной силой.

 

Потенциал электростатического поля, создаваемого точечным зарядом Q на расстоянии r, определяется (с точностью до произвольной константы С) формулой j = + С. Это не приводит к недоразумениям, т.к. физика процессов зависит не от потенциала, а от разности потенциалов. Разность потенциалов не зависит от выбора постоянной константы

[(j₁ + C) - (j₂ + C)] = (j₁ - j₂).

Если принять некоторую точку поля за нулевой уровень потенциала, тогда потенциал принимает однозначный вид:

j = .

В физике за нулевой уровень потенциала поля заряда принят потенциал в бесконечности. В радиотехнической и электротехнической практике за нулевой уровень потенциала обычно принимается потенциал Земли. При заземлении кожух и несущие конструкции прибора приобретает потенциал Земли, что обеспечивает безопасность эксплуатации.

Из выражения A = q (j₁ - j₂) следует, что разность потенциалов двух точек поля равна работе поля по перенесению единичного заряда из первой во вторую точку: (j₁ - j₂) = 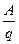. Таким образом, единицей потенциала служит 1 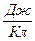. Единица потенциала (1 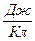) имеет собственное название – вольт:

1 В = 1 .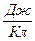

Полезно обратить внимание на структурную и содержательную аналогию в формулах для электростатического поля

F = qE и A = q (j₁ - j₂),

и поля силы тяжести (поле силы тяжести также потенциальное поле)

F = mgи A = m(gh₁ - gh₂).

 

3.1.5. Потенциальная энергия взаимодействия зарядов

Потенциальная энергия взаимодействия системы из двух зарядов. Из уравнения (15) следует, что работу можно представить убылью скалярной функции W(r) = :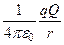

A = 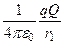- = W(r₁) - W(r₂) = -DW.

Функция W(r) называется потенциальной энергией взаимодействия зарядов Q и q, а работа равна убыли потенциальной энергии (-DW) взаимодействия зарядов.

Потенциальная энергия взаимодействия системы, содержащей более двух зарядов. Вначале рассмотрим пример системы из трех взаимодействующих зарядов. Потенциальная энергия такой системы

W = W₁₂ + W₁₃ + W₂₃,

где: W₁₂ – поте