 |
Главная |
Природа электромагнитной индукции
|
из
5.00
|
 Явление электромагнитной индукции заключается в возникновении ЭДС и соответствующего тока в проводящем контуре при изменении потока индукции магнитного поля через мысленную поверхность, натянутую на контур. ЭДС в явлении электромагнитной индукцииназывается ЭДС индукции. Будем обозначать ЭДС индукции буквой x. Электрический ток, порождаемый в проводящем контуре, называется индукционным током.
Явление электромагнитной индукции заключается в возникновении ЭДС и соответствующего тока в проводящем контуре при изменении потока индукции магнитного поля через мысленную поверхность, натянутую на контур. ЭДС в явлении электромагнитной индукцииназывается ЭДС индукции. Будем обозначать ЭДС индукции буквой x. Электрический ток, порождаемый в проводящем контуре, называется индукционным током.
Закон электромагнитной индукции – закон Фарадея – выражается формулой:
x = 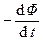 . (1)
. (1)
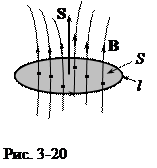
В (1) Ф = B S º B S cosa – поток индукции магнитного поля через поверхность, натянутую на контур; S = nS, где n – нормаль к поверхности S; a - угол между нормалью к поверхности S и вектором B(рис. 3-20). Направление вектора-площади S = nS и направление обхода контура связаны между собой правилом правого винта. Знак минус в (1) является правилом Ленца. Единицей магнитного потока служит вебер (Вб):
1Вб = 1Тл×м2.
Из определения потока вектора B= B S cosa следует, что приращение потока через проводящий контур 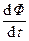 можно осуществить тремя способами: 1) изменением величины индукции магнитного поля во времени
можно осуществить тремя способами: 1) изменением величины индукции магнитного поля во времени  при неподвижном контуре; 2) изменением площади
при неподвижном контуре; 2) изменением площади 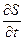 в постоянном магнитном поле, т.е. деформацией проводящего контура; 3) изменением ориентации контура
в постоянном магнитном поле, т.е. деформацией проводящего контура; 3) изменением ориентации контура 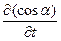 в постоянном магнитном поле, т.е. поворотом (вращением) проводящего контура в постоянном магнитном поле. Заметим, последние два случая – изменение величины площади контура и изменение ориентации контура – можно выразить изменением вектора-площади
в постоянном магнитном поле, т.е. поворотом (вращением) проводящего контура в постоянном магнитном поле. Заметим, последние два случая – изменение величины площади контура и изменение ориентации контура – можно выразить изменением вектора-площади 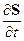 .
.
Последние два способа изменения потока вектора B через контур – при изменении площади контура, т.е. деформации контура и изменении ориентации контура в магнитном поле, т.е. вращении контура в магнитном поле – связаны с перемещением элементов контура в магнитном поле. В этих двух случаях физика возникновения ЭДС индукции x в проводящем контуре обусловлена действием магнитной силы Лоренца на свободные заряды в объеме перемещающихся элементов контура (рис 22).
 |
На рис. 3-21-а приведен второй случай – случай деформации контура. Здесь перемычка cd перемещается влево со скоростью vи площадь S контура abcd изменяется. На рисунке магнитное поле направлено за чертеж. Выделим положительный заряд q в проводнике. На этот заряд действует магнитная сила ЛоренцаFм = q[v, B] и заряд будет перемещаться вверх по рисунку. Произойдет разделение зарядов и на концах перемещающегося проводника возникнет ЭДС, что приведет к индуцированию тока в контуре. Магнитная сила играет роль сторонней силы. Этой сторонней силе соответствует стороннее электрическое поле E = 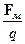 = [v, B]. Аналогичная ситуация наблюдается в третьем случае - при вращении контура в постоянном магнитном поле. Изменение ориентации вектора-площади Sотносительно вектора B, т.е. изменение угла a, означает перемещение элементов контура в магнитном поле. Это также обусловливает возникновение магнитной силы Лоренца (рис. 3-21-б), действующей на заряды в всех движущихся частях контура, что приводит к возникновению ЭДС индукции в контуре.
= [v, B]. Аналогичная ситуация наблюдается в третьем случае - при вращении контура в постоянном магнитном поле. Изменение ориентации вектора-площади Sотносительно вектора B, т.е. изменение угла a, означает перемещение элементов контура в магнитном поле. Это также обусловливает возникновение магнитной силы Лоренца (рис. 3-21-б), действующей на заряды в всех движущихся частях контура, что приводит к возникновению ЭДС индукции в контуре.
Циркуляция электрического поля в определится выражением:
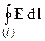 =
=  , (2)
, (2)
где l – контур, который пронизывается потоком вектора индукции магнитного поля.
В первом случае ЭДС в неподвижном контуре обусловлена изменением магнитного поля – переменное магнитное поле порождает вихревое электрическое поле, индуцирующее электрический ток в проводящем контуре (в замкнутом проводнике). Подчеркнем, вихревое электрическое поле порождается переменным магнитным полем независимо от наличия проводящего контура. Сам по себе проводящий контур необходим только в роли установки обнаружения этого вихревого электрического поля. Циркуляция вектора напряженности E вихревого электрического поля по произвольному контуру, порождаемого переменным магнитным полем, определяется уравнением
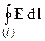 =
=  , где
, где 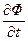 =
=  .
.
Итак, циркуляция вектора напряженности вихревого электрического поля E, порождаемого переменным магнитным полем выражается уравнением:
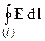 = -
= -  , (3)
, (3)
 где S – произвольная поверхность, натянутая на контур, пронизываемая переменным магнитным полем (рис. 3-22).
где S – произвольная поверхность, натянутая на контур, пронизываемая переменным магнитным полем (рис. 3-22).
Подчеркнем еще раз, контур не обязательно должен быть материализованным проводящим контуром, контур может быть и мысленным.
Итак, закон Фарадея (1) можно представить через циркуляцию вектора напряженности в виде
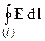 = -
= -  +
+  . (3*)
. (3*)
Подчеркнем, физика слагаемых в правой части уравнения (3*), определяющих явление электромагнитной индукции, совершенно разная. Каждый из слагаемых описывает разные по физическому содержанию причины возникновения индукционного тока в проводящем контуре. В движущемся контуре ЭДС индукции возникает вследствие действия силы Лоренца на заряды в проводнике (слагаемое  );в неподвижном контуре – представлением о порождении вихревого электрического поля переменным магнитным полем (слагаемое
);в неподвижном контуре – представлением о порождении вихревого электрического поля переменным магнитным полем (слагаемое  ). Однако в том и другом случае индукционный ток в проводящем контуре возникает при изменении магнитного потока через контур.
). Однако в том и другом случае индукционный ток в проводящем контуре возникает при изменении магнитного потока через контур.
Правило Ленца в (1) определяет направление индукционного тока: индукционный ток имеет такое направление, чтобы препятствовать причине, его вызвавший. Например, на рис. 3-21-а индукционный ток направлен против часовой стрелки. Этот ток создает свой магнитный поток сквозь рамку, направленный против потока вектора индукции B внешнего магнитного поля, который порождает индукционный ток.
3.3.2. Самоиндукция. Индуктивность проводника
ЭДС индукции в проводящем контуре возникает всегда, когда магнитный поток изменяется в контуре. Если ток в контуре изменяется (например: в контуре проходят переходные процессы, связанные с зарядкой конденсатора; по контуру течет переменный ток и т.п.), то порождаемый этим током магнитное поле (и соответствующий магнитный поток) также является переменным. В контуре появляется ЭДС индукции, который здесь называется ЭДС самоиндукции.
В отсутствии ферромагнетиков рядом с проводящим контуром магнитный поток Ф пропорционален току I в контуре:
Ф = LI, (4)
где коэффициент пропорциональности L называется индуктивностью контура. Единицей индуктивности служит генри: 1Гн = 1  .
.
ЭДС самоиндукции имеет вид:
xS = 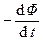 =
=  . (5)
. (5)
Если индуктивность L остается постоянным в переменном магнитном потоке, то ЭДС самоиндукции примет вид:
xS = 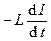 при L = const. (5*)
при L = const. (5*)
В качестве примера приведем расчет индуктивности соленоида с числом витков на единицу длины соленоида n. Объем соленоида V. Магнитная проницаемость магнетика в объеме соленоида m.
Решение. Индуктивность L = 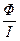 . Зададим ток I, тогда индукция магнитного поля в соленоиде B = mm0nI. Магнитный поток через один виток Ф1 = BS =mm0nIS, а полный поток Ф = N Ф1 = nlФ1 = nlmm0nIS =mm0n2IV, т.к. V = lS, где l – длина соленоида. Имеем:
. Зададим ток I, тогда индукция магнитного поля в соленоиде B = mm0nI. Магнитный поток через один виток Ф1 = BS =mm0nIS, а полный поток Ф = N Ф1 = nlФ1 = nlmm0nIS =mm0n2IV, т.к. V = lS, где l – длина соленоида. Имеем:
L = 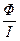 =mm0n2V .
=mm0n2V .
Обратите внимание, индуктивность соленоида определяется геометрией проводника (в данном примере – геометрией соленоида n2V) и магнитными свойствами среды m.
3.3.3. Магнитная энергия
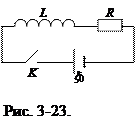 1. Магнитная энергия электрического тока. Пусть электрическая цепь содержит сопротивление R, индуктивность L и источник тока x0 (рис. 3-23).
1. Магнитная энергия электрического тока. Пусть электрическая цепь содержит сопротивление R, индуктивность L и источник тока x0 (рис. 3-23).
Замкнем цепь, ток будет возрастать, и в индуктивности L возникнет ЭДС самоиндукции xS. Закон Ома запишется в виде IR = x0 + xS. Определим работу источника тока dA за время dt. Для этого умножим уравнение закона Ома на Idt:
x0 Idt = I2Rdt - xS Idt или dA = dQ + IdФ (т.к. xS = 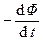 ).
).
Из последнего уравнения видно, что в процессе приближения тока к стационарному режиму, работа источника тока идет не только на нагревание цепи (член dQ, определяющий джоулево тепло), но дополнительно и на работу против ЭДС самоиндукции (член IdФ). Итак,
dA(доп) = IdФ. (6)
Из (3.4) в отсутствии ферромагнетиков имеем соотношение dФ = LdI. Тогда (6) примет вид: dA(доп) = L IdI (6*)
Проинтегрировав (6*), получим:
A(доп) = 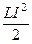 .
.
Итак, работа источника тока в процессе установления стационарного режима идет на джоулево тепло и, дополнительно, на создание магнитного поля. Таким образом, магнитная энергия электрического тока выражается формулами: W = 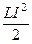 =
=  =
= 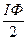 . (7)
. (7)
2. Энергия магнитного поля.
Определим энергию магнитного поля длинного соленоида. Индуктивность соленоида L=mm0n2V. Подставим эту формулу в (7), получим:
W = 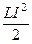 =
=  mm0n2 I2 V.
mm0n2 I2 V.
Так как B = mm0nI (смотрите пример в §3.2.4) и B =mm0H, то имеем:
W = 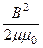 V =
V =  V =
V =  V = wV, (8)
V = wV, (8)
где w = 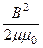 , или w =
, или w =  , или w =
, или w =  - разные формы представления плотности энергии магнитного поля. Если плотность энергии задана, то энергия магнитного поля в объеме V выражается интегралом. Например:
- разные формы представления плотности энергии магнитного поля. Если плотность энергии задана, то энергия магнитного поля в объеме V выражается интегралом. Например:
W = 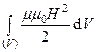 . (3.9)
. (3.9)
Разумеется, аналогичную форму записи энергии магнитного поля в объеме V имеем и с остальными формулами плотности энергии:
W =  , W =
, W =  . (9*)
. (9*)
Формулы (9) и (9*) указывают, что магнитная энергия, так же как и электрическая энергия, локализована в пространстве.
УРАВНЕНИЯ МАКСВЕЛЛА
3.4.1. Объекты теории электромагнитного поля. Уравнения
|
из
5.00
|
Обсуждение в статье: Природа электромагнитной индукции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

