Падании волны из диэлектрика

Пусть плоскость поляризации электромагнитной волны во второй среде (т.е. плоскость, образованная вектором Пойнтинга П₂ и вектором напряженности E₂) образуют некоторый угол y с плоскостью преломления. В этом случае вектораE₂ и H₂ имеют ненулевые проекции на оси x и y. Электрическая и магнитная составляющие электромагнитной волны во второй среде определяются уравнениями (133), (133*). Выпишем эти уравнения еще раз

= , (141)

= . (142)

При горизонтальной (нормальной) поляризации = . При произвольном расположении плоскости поляризации относительно плоскости преломления имеются проекции на оси координат x и y.

Уравнения (141) и (142) структурно одинаковые. В этой связи, при рассмотрении особенностей распространения волны во второй проводящей среде, уравнения (141) и (142) удобно представить одним «обобщенным» уравнением: = , (143)

где для (141) = , для (142) = .

Электромагнитная волна падает наклонно на границу сред диэлектрик-проводник под углом падения q и преломляется под углом f (рис. 3-52). По закону преломления = 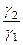. (144)

Пусть первая среда является практически идеальным диэлектриком (проводимость g₁ = 0), вторая среда – проводник с проводимостью g₂. В проводящей среде имеется затухание волны, характеризуемое коэффициентом затухания a₂ ¹ 0 [см. уравнения (83), (84)]. Коэффициент затухания в первой среде a₁ = 0. Постоянные распространения в средах

g₁ = ik₁ , g₂ = a₂ + ik₂. (145)

Покажем, что:

1) независимо от угла падения q, плоскости равных амплитуд преломленной волны в проводящей среде параллельны плоскости раздела сред. Уравнение поверхности равных амплитуд z = const (рис. 3-52);

2) если модули постоянных распространения отвечают условию

úg₂ê >> úg₁ê,

где úg₁ê= k₁, úg₂ê= 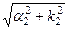, то поверхности равных амплитуд и поверхности равных фаз волны совпадают, а угол преломления близка к нулю f » 0 (на рис. 3-52 приведена ситуация, когда úg₂êи úg₁êодного порядка).

1. Угол падения q задается экспериментатором и является по своему смыслу вещественным числом. Угол преломления f, в соответствии с законом преломления (144) и соотношениями (145), - комплексная величина. Следовательно, cosf в уравнении (4.143) можно представить как комплексную величину cosf = p +iq.

По закону преломления sinf = sinq.

Постоянные распространения в средах представлены соотношениями (145).

Подставим эти соотношения в (143), получим:

= = = =

= = .

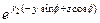Для краткости записи введем обозначения вещественных чисел

a₂p - k₂q = b > 0, a₂q - k₂p = c, k₁sinq = h

Имеем: = или

= (146)

Из уравнения преломленной волны (146) следует, что волна затухает строго в отрицательном направлении оси z (множитель в отрицательном направлении оси z убывает). Это означает, что независимо от угла падения q, плоскости равных амплитуд в проводящей среде параллельны плоскости раздела сред. Уравнение поверхности равных амплитуд можно представить уравнением z = const. На рис. 3-52 в качестве примера показана одна такая плоскость, параллельная плоскости раздела сред, и, следовательно, перпендикулярная оси z.

Обратите внимание, так как преломленная волна является плоской волной, то поверхность равных фаз (вектор Пойнтинга П₂ перпендикулярен поверхности равных фаз волны) не совпадает с поверхностью равных амплитуд (рис. 3-52). Из уравнения (146) следует, что поверхность равных фаз определяется уравнением

cz - hy = const.

На поверхности равных фаз амплитуда волны не является постоянной величиной.

2. Допустим, второй средой является хороший проводник, например, металл (первая среда – диэлектрик). Это соответствует условию

úg₂ê >> úg₁ê. (147)

Из закона преломления sinf = sinq следует, что при выполнении условии (147) при любых углах падения q модуль комплексного угла преломления úf ê® 0. Следовательно, в уравнении (143) при выполнении (147) можно использовать приближенные оценки:

sinf » 0 , cosf » 1.

При этих оценках уравнение для произвольной составляющей электромагнитного поля (143) запишется в виде:

= = . (148)

Из (148) следует, что при любых углах падения q волна электромагнитная волна во второй среде – проводнике – распространяется практически в направлении оси z [перпендикулярно плоскости раздела сред (úf ê» 0)]. В этой связи можно считать, что плоскость равных фаз и плоскость равных амплитуд в проводнике совпадают. Такая волна называется однородной.

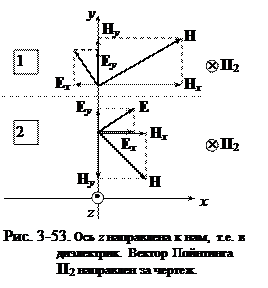
Таким образом, при произвольной ориентации плоскости поляризации электромагнитной волны, прошедшей из диэлектрика в проводник, векторы E и H будут обладать компонентами только по осям x и y (рис. 3-53):

E_x2 и E_y2; H_x2 и H_y2.

Расположение векторовE и H относительно осей координат может быть различной (в качестве примера на рис. 3-53 и рис. 3-54 показаны по две ситуации).

Если ось z направить в сторону диэлектрика (так же, как и на рис. 3-52), то по определению понятия волнового сопротивления и знаков компонент векторовE и H имеем соотношения (см. рис. 3-53):

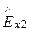= - , (149)

= (150)

Напомним, индекс «2» означает, что рассматривается волна в проводящей среде.

Если ось z направить в сторону проводника, то в соответствии со знаками компонент (см. рис. 3-54) имеем соотношения (см. также рис. 3-55):

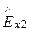= , (151)

= - (152)

3.8.4. Затуханиеэлектромагнитной волны в проводящей среде.