 |
Главная |
Числовые последовательности и операции над ними
|
из
5.00
|
Определение. Если каждому натуральному числу 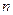 поставлено в соответствие по некоторому закону
поставлено в соответствие по некоторому закону  определённое число
определённое число 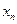 , то говорят, что на множестве всех натуральных чисел
, то говорят, что на множестве всех натуральных чисел 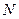 задана последовательность
задана последовательность

Общий член последовательности является функцией от 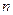 .
.
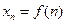
Таким образом, последовательность является функцией натурального аргумента.
Задать последовательность можно различными способами. Необходимо только, чтобы был указан способ получения любого члена последовательности.
Пример.
 или
или 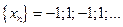 .
.
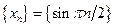 или
или 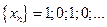
Для последовательностей можно определить следующие операции:
1) Умножение последовательности на число  :
: 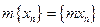 , т.е.
, т.е. 
2) Сложение (вычитание) последовательностей:  .
.
3) Произведение последовательностей: 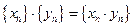 .
.
4) Частное последовательностей:  при
при  .
.
Ограниченные и неограниченные последовательности
Определение. Последовательность  называется ограниченной, если существует такое число
называется ограниченной, если существует такое число  , что для любого
, что для любого 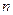 справедливо неравенство:
справедливо неравенство:
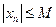
т.е. все члены последовательности принадлежат отрезку 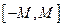 .
.
Определение. Последовательность  называется ограниченной сверху, если для любого
называется ограниченной сверху, если для любого 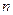 существует такое число
существует такое число 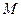 , что
, что
 .
.
Определение. Последовательность  называется ограниченной снизу, если для любого n существует такое число
называется ограниченной снизу, если для любого n существует такое число 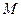 , что
, что

Пример.  – ограничена снизу {1, 2, 3, … }.
– ограничена снизу {1, 2, 3, … }.
Определение. Число 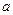 называется пределом последовательности
называется пределом последовательности  , если для любого положительного
, если для любого положительного  существует такой номер
существует такой номер 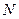 , что для всех
, что для всех  выполняется неравенство:
выполняется неравенство:
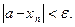
Обозначение: 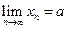 . В этом случае говорят, что последовательность
. В этом случае говорят, что последовательность  сходится к
сходится к 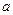 при
при  .
.
Пример. Доказать, что предел последовательности  .
.
Пусть при  верно
верно 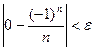 , т.е.
, т.е.  . Это верно при
. Это верно при 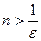 , таким образом, если за
, таким образом, если за 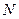 взять целую часть от
взять целую часть от 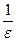 , то утверждение, приведенное выше, выполняется.
, то утверждение, приведенное выше, выполняется.
Пример. Показать, что при  последовательность
последовательность  имеет пределом число 2. Имеем
имеет пределом число 2. Имеем 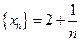 ;
; 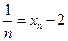 .Для любого положительного числа
.Для любого положительного числа 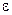 существует такое натуральное число
существует такое натуральное число 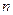 , что
, что 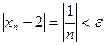 , т.е.
, т.е. 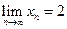 .
.
Теорема. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что последовательность  имеет два предела
имеет два предела 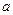 и
и 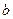 , не равные друг другу.
, не равные друг другу.

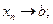
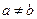 .
.
Тогда по определению существует такое число  , что
, что
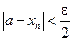 и
и  .
.
Запишем выражение: 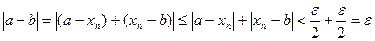 .
.
Так как  - любоеположительноечисло, то
- любоеположительноечисло, то 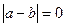 , т.е.
, т.е. 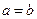 . Теорема доказана.
. Теорема доказана.
Теорема. Если  , то
, то 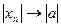 .
.
Доказательство. Из  следует, что
следует, что 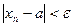 . В то же время:
. В то же время:
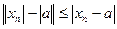 , т.е.
, т.е. 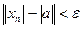 , т.е.
, т.е. 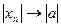 . Теорема доказана.
. Теорема доказана.
Теорема. Если  , то последовательность
, то последовательность  ограничена.
ограничена.
Необходимо отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например, последовательность 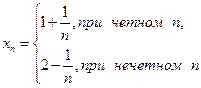 не имеет предел. В то же время
не имеет предел. В то же время 
Монотонные последовательности
Определении
1) Если 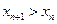 для всех
для всех 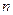 , то последовательность называется возрастающей.
, то последовательность называется возрастающей.
2) Если 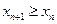 для всех
для всех 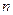 , то последовательность называется неубывающей.
, то последовательность называется неубывающей.
3) Если 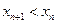 для всех
для всех 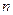 , то последовательность называется убывающей.
, то последовательность называется убывающей.
4) Если 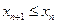 для всех
для всех 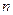 , то последовательность называется невозрастающей.
, то последовательность называется невозрастающей.
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример.  – убывающая и ограниченная;
– убывающая и ограниченная; 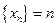 – возрастающая и неограниченная.
– возрастающая и неограниченная.
Пример. Доказать, что последовательность 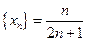 монотонная и возрастающая.
монотонная и возрастающая.
Найдем  -й член последовательности
-й член последовательности 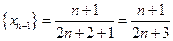
Найдем знак разности: 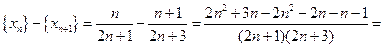
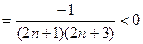 , т.к.
, т.к. 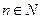 , то знаменатель положительный при любом
, то знаменатель положительный при любом 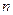 .
.
Таким образом, 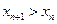 . Последовательность возрастающая, что и следовало доказать.
. Последовательность возрастающая, что и следовало доказать.
Пример. Выяснить является возрастающей или убывающей последовательность
 .
.
Найдём  . Определим разность
. Определим разность 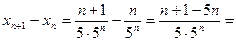
 , так как
, так как 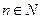 , то
, то  , т.е.
, т.е. 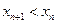 . Последовательность монотонно убывает.
. Последовательность монотонно убывает.
Заметим, что монотонные последовательности являютс ограниченными по крайней мере с одной стороны.
Теорема. Монотонная ограниченная последовательность имеет конечный предел.
Доказательство. Рассмотрим монотонную неубывающую последовательность

Эта последовательность ограничена сверху: 
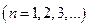 , где
, где 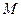 – некоторое число. Так как любое ограниченное сверху, числовое множество имеет точную верхнюю грань, то для любого
– некоторое число. Так как любое ограниченное сверху, числовое множество имеет точную верхнюю грань, то для любого  существует число
существует число 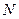 такое, что
такое, что 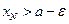 , где
, где 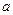 – точная верхняя грань множества значений последовательности.
– точная верхняя грань множества значений последовательности.
Так как  - неубывающая последовательность, то при
- неубывающая последовательность, то при 
 ,
,
 . Отсюда
. Отсюда 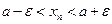 или
или  или
или  , т.е.
, т.е. 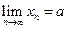 .
.
Для остальных монотонных последовательностей доказательство аналогично. Теорема доказана.
Число е
Рассмотрим последовательность 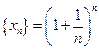 .Если последовательность
.Если последовательность  монотонная и ограниченная, то она имеет конечный предел. По формуле бинома Ньютона:
монотонная и ограниченная, то она имеет конечный предел. По формуле бинома Ньютона:
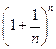
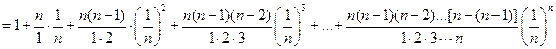
или
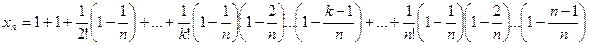
Покажем, что последовательность  – возрастающая. Действительно, запишем выражение
– возрастающая. Действительно, запишем выражение 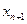 и сравним его с выражением
и сравним его с выражением 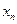 :
:
 Каждое слагаемое в выражении
Каждое слагаемое в выражении 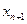 больше соответствующего значения
больше соответствующего значения 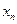 , и, кроме того, у последовательности
, и, кроме того, у последовательности 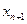 добавляется еще одно положительное слагаемое. Таким образом, для любого натурального числа
добавляется еще одно положительное слагаемое. Таким образом, для любого натурального числа 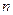
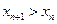 , т.е последовательность
, т.е последовательность  возрастающая.
возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: 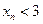 .
.
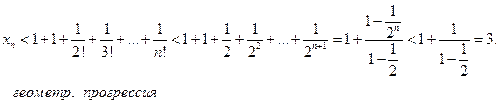
Таким образом, последовательность 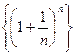 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
 .
.
Число 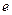 является трпансцендентным числом и приблизительно равно
является трпансцендентным числом и приблизительно равно

Число 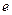 является основанием натурального логарифма.
является основанием натурального логарифма.
|
из
5.00
|
Обсуждение в статье: Числовые последовательности и операции над ними |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

