 |
Главная |
Производная и дифференциал функции
|
из
5.00
|
Производная функции, ее геометрический смысл
Определение. Производной функции 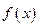 в точке
в точке 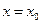 называется предел, если он существует, отношения приращения функции в точке
называется предел, если он существует, отношения приращения функции в точке 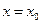 к приращению аргумента
к приращению аргумента 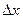 в этой точке, когда последнее стремится к нулю:
в этой точке, когда последнее стремится к нулю:
 ,
,
где  - приращение аргумента в точке
- приращение аргумента в точке 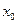 , а
, а 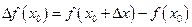 - соответствующее этому приращению приращение функции
- соответствующее этому приращению приращение функции 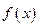 в этой точке.
в этой точке.
 у
у
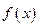
 P
P

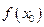 M
M

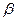
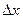
0 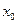
 x
x
Пусть функция 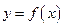 определена на некотором промежутке
определена на некотором промежутке 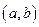 и имеет во внутренней точке
и имеет во внутренней точке 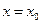 этого промежутка конечную производную. Пусть
этого промежутка конечную производную. Пусть  - точка графика функции
- точка графика функции 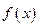 , соответствующая абсциссе
, соответствующая абсциссе 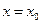 , а
, а  - произвольная точка графика функции.
- произвольная точка графика функции.
Касательной к кривой в точке 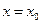 называется предельное положение секущей
называется предельное положение секущей 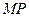 , когда точка
, когда точка  стремится к точке
стремится к точке 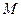 по кривой с любой стороны.
по кривой с любой стороны.
Обозначим через  угол наклона секущей МР к положительному направлению оси
угол наклона секущей МР к положительному направлению оси  . Тогда
. Тогда  . Находим
. Находим
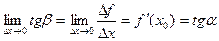 ,
,
где 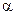 - угол наклона касательной к графику функции
- угол наклона касательной к графику функции 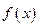 в точке
в точке  .
.
Угол между кривыми в их общей точке определяется как угол между касательными, проведенными к этим кривым в их общей точке.
Уравнение касательной к кривой в точке 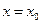 имеет вид:
имеет вид: 
Уравнение нормали к кривой в точке 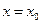 имеет вид:
имеет вид:  .
.
Функция 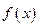 имеющая конечную производную в точке
имеющая конечную производную в точке 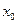 называется дифференцируемой в этой точке.
называется дифференцируемой в этой точке.
Односторонние производные функции в точке
Определение. Правой (левой) производной функции 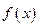 в точке
в точке 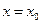 называется правый (левый) предел
называется правый (левый) предел

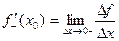
при условии, что этот предел существует.
Если функция 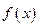 имеет производную в некоторой точке
имеет производную в некоторой точке 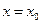 , то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке
, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке 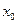 , а во- вторых, даже если функция непрерывна в точке
, а во- вторых, даже если функция непрерывна в точке 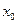 , она может быть в ней не дифференцируема.
, она может быть в ней не дифференцируема.
Например:  - имеет в точке
- имеет в точке 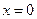 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция 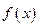 имеет производную в точке
имеет производную в точке 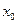 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Очевидно, что это условие не является достаточным.
Основные правила дифференцирования
Пусть 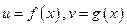 - функции, дифференцируемые в точке
- функции, дифференцируемые в точке 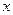 . Тогда:
. Тогда:
1) 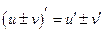
2) 
3)  , если v ¹ 0
, если v ¹ 0
Эти правила могут быть доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)  , 9)
, 9) 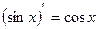 ,
,
2) 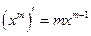 , 10)
, 10)  ,
,
3)  , 11)
, 11) 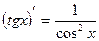 ,
,
4)  , 12)
, 12) 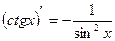 ,
,
5)  , 13)
, 13)  ,
,
6) 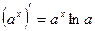 , 14)
, 14)  ,
,
7)  , 15)
, 15)  ,
,
8) 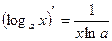 , 16)
, 16)  .
.
Производная сложной функции
Теорема.Пусть  , причем область значений функции
, причем область значений функции  входит в область определения функции
входит в область определения функции  .Тогда
.Тогда 
Доказательство. Имеем
 .
.
Переходя к пределу в обеих частях при  получим:
получим:
 ,
,
(с учетом того, что если  , то
, то  , т.к.
, т.к.  – непрерывная функция)
– непрерывная функция)
Тогда  . Теорема доказана.
. Теорема доказана.
|
из
5.00
|
Обсуждение в статье: Производная и дифференциал функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

