 |
Главная |
Начальные и центральные моменты непрерывной случайной величины, асимметрия и эксцесс. Мода и медиана
|
из
5.00
|
В прикладных задачах, например в математической статистике, при теоретическом изучении эмпирических распределений, отличающихся от нормального распределения, возникает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.
Определение. Мода непрерывной случайной величины ( Мо (X)) – это её наиболее вероятное значение, для которого вероятность pi или плотность вероятности f(x) достигает максимума.
Определение. Медиана непрерывной случайной величины X (Me(X)) – это такое её значение, для которого выполняется равенство:
P (X < Me (X)) = P (X >Me (X)) = 
| Me (X) |
| x |
| f(x) |
Геометрически вертикальная прямая x = Me (X) делит площадь фигуры под кривой на две равные части.
В точке X = Me (X), функция распределения F (Me (X)) = 
Пример:
Найти моду Mo, медиану Me и математическое ожидание M случайной величины X с плотностью вероятности f(x) = 3x2, при x Î [ 0; 1 ].
Решение:
1. Плотность вероятности f (x) максимальна при x = 1, т.е. f (1) = 3, следовательно, Mo (X) = 1 на интервале [ 0; 1 ].
2. Для нахождения медианы обозначим Me (X) = b.
Так как Me (X) удовлетворяет условию P (X < Me (X)) =  ,
,
то P (-∞ < X < b) =  =
=  =
=
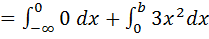 =
= 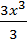
 = b3 =
= b3 =  .
.
b3 =  ; b =
; b =  » 0,79
» 0,79
3. M (X) =  =
=  +
+  =
=
=  =
= 
 =
=  = 0,75
= 0,75
Отметим получившиеся 3 значения Mo (x), Me (X), M (X) на оси Ox:

Определение. Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Определение. Эксцессом теоретического распределения называется величина, определяемая равенством:
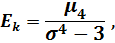
где  ‒ центральный момент четвертого порядка.
‒ центральный момент четвертого порядка.
Для нормального распределения  . При отклонении от нормального распределения асимметрия положительна, если "длинная" и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 1, а, б).
. При отклонении от нормального распределения асимметрия положительна, если "длинная" и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 1, а, б).

Эксцесс характеризует "крутизну" подъема кривой распределения по сравнению с нормальной кривой: если эксцесс положителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину.
Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дисперсии для нормального и теоретического распределений.
Пример. Пусть дискретная случайная величина Х задана законом распределения:

Найти: асимметрию и эксцесс теоретического распределения.
Решение:
Найдем сначала математическое ожидание случайной величины:

Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение:

Теперь по формулам находим искомые величины:

В данном случае "длинная" часть кривой распределения расположена справа от моды, причем сама кривая является несколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.
Неравенство Чебышева.
Теорема.Для произвольной случайной величины Х и любого числа
Ԑ>0 справедливы неравенства:


‒ вероятность противоположного неравенства.
Пример.
Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратичное отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000 л, используя неравенство Чебышева.
Решение:
Пусть X –расход воды на животноводческой ферме (л).
По условию М(Х) = 1000.
Дисперсия D(X) = 

 . Так как границы интервала 0
. Так как границы интервала 0  X
X  2000 симметричны относительно математического ожидания М(Х) = 1000, то для оценки вероятности искомого события можно применить неравенство Чебышева:
2000 симметричны относительно математического ожидания М(Х) = 1000, то для оценки вероятности искомого события можно применить неравенство Чебышева:


То есть не менее, чем 0,96  .
.
Для биномиального распределения неравенство Чебышева примет вид:

так как M(X) = np; D(X)=npq.
|
из
5.00
|
Обсуждение в статье: Начальные и центральные моменты непрерывной случайной величины, асимметрия и эксцесс. Мода и медиана |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

