 |
Главная |
Мода случайной величины
|
из
5.00
|
Модой  (х) случайной величины называется наиболее вероятное ее значение, то есть значение, вероятность которого максимальна.
(х) случайной величины называется наиболее вероятное ее значение, то есть значение, вероятность которого максимальна.
Если максимальные вероятности принимают несколько значений случайных величин, то такое распределение называется полимодальным.
Пример.
Дискретная случайная величина X задана законом распределения:

| ‒1 | |||

| 0,1 | 0,2 | 0,1 | 0,6 |
Найти: числовые характеристики случайной величины: M(X), D(X), Ϭ(X),  (х).
(х).
Решение:
Построим многоугольник распределения данной случайной величины.

1. Математическое ожидание:

2. Дисперсия:


3. Средне квадратическое откланение:

4.  так как максимальная вероятность этого значения равна 0,6.
так как максимальная вероятность этого значения равна 0,6.
Моменты случайных величин
Начальным моментом k ‒ го порядка называется математическое ожидание k ‒ й степени случайной величины:

при k=1; 
Центральным моментом  случайной величины (X) называется математические ожидание k‒й степени отклонения случайной величины (Х) от ее математического ожидания:
случайной величины (X) называется математические ожидание k‒й степени отклонения случайной величины (Х) от ее математического ожидания:
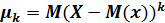 ,
,
при k=2,  =D(Х).
=D(Х).
Функция распределения случайной величины.
Функцией распределения случайной величины (F(x)) – называется вероятность того, что случайная величина X примет значения меньше x. Следовательно,
 ,
,
т.е. геометрически значения X будут левее x:
x
Так как F(x) – вероятность события X < x, то

Пример
| xi | ||||
| pi | 0,4 | 0,1 | 0,3 | 0,2 |
Найти функцию распределения F(x) и построить график.
Решение:
1 4 5 7
1. Если x ≤ 1,то F(x) = 0.
2. Если 1< x ≤ 4, например, x=2, то F(2) = P(X < 2 ) = 0,4
3. Если 4 < x ≤ 5, например, x = 4,5, то F(4,5) = P(X<4,5) = P(X=1)+P(X=4)=0,4+0,1=0,5
4.Если 5 < x ≤ 7, например x=6, то F(6)=P(X<6)=P(X=1)+P(X=4)+P(X=5)=0,4+0,1+0,3=0,8
5. Если x > 7, например x =8, то F(8)=P(X<8)=P(X=1)+P(X=4)+P(X=5)+P(X=7)= 0,4+0,1+0,3+0,2=1
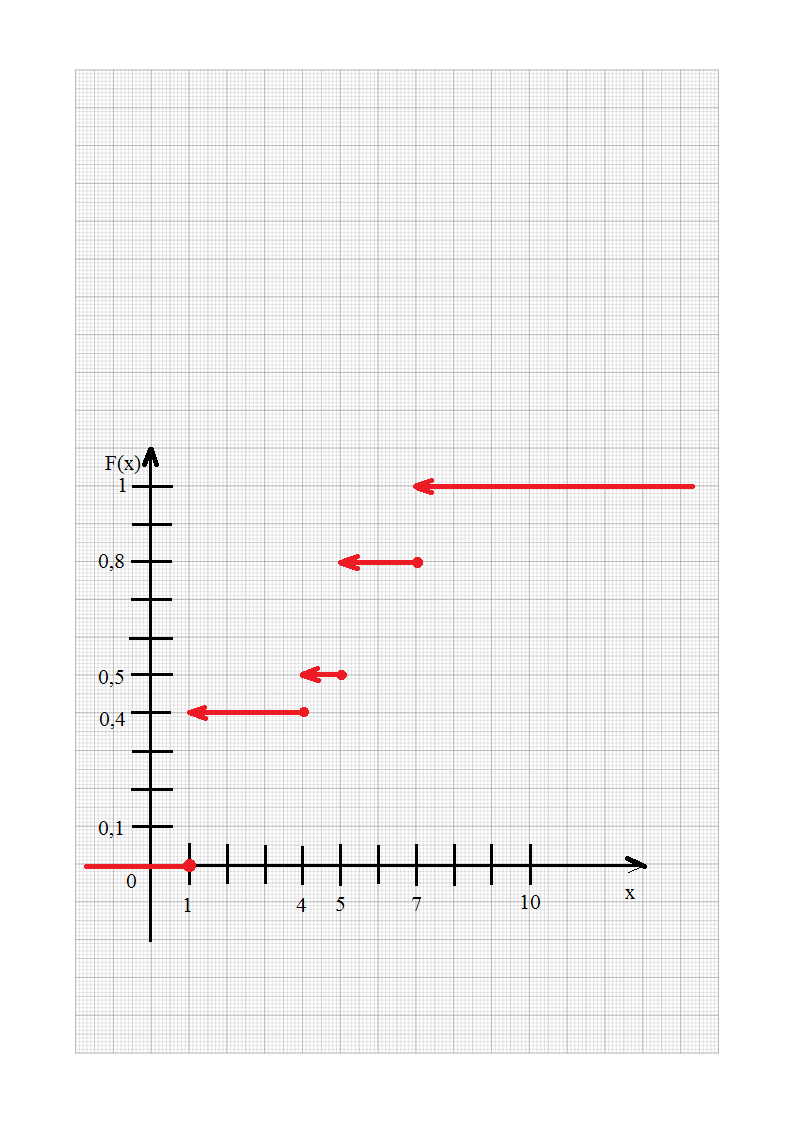
0; если x ≤ 1
0,4; если 1< x ≤ 4
F(x) = 0,5 если 4 < x ≤ 5
0,8; если 5 < x≤ 7
1; если x > 7
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.
Биномиальный закон распределения (биномиальное распределение) дискретных случайных величин.
Дискретная случайная величина Х распределена по биномиальному закону, если она принимает значения 0,1,2…,m…,n… с вероятностями, которые находятся по формуле Бернулли:


| … | m | … | n | ||

| 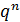
| 
| … | 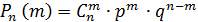
| … | 
|

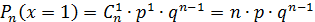
………………………………………………...

Теорема. Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равняется произведению числа всех испытаний на вероятность наступления события в отдельном испытании, то есть
 .
.
Дисперсия равняется произведению числа всех испытаний на вероятность наступления и не наступления события в отдельном испытании, то есть
 .
.
Пример.
По статистическим данным известно, что вероятность рождения мальчика составляет: p = 0,515.
Составить закон распределения числа мальчиков в семье с пятью детьми. Найти математическое ожидание  , дисперсию
, дисперсию 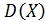 , среднее квадратическое отклонение
, среднее квадратическое отклонение  и моду
и моду  .
.
Решение:
X ‒ случайная величина ‒ число мальчиков в семье с пятью детьми.
Составим закон распределения числа мальчиков в семье с пятью детьми:

| ||||||

| 0,026835 | 0,142475 | 0,302579 | 0,321296 | 0,170585 | 0,036227 |







Проверка:


1. Математическое ожидание:

2. Дисперсия:

3. Среднее квадратическое отклонение:
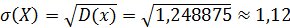
4.  так как при m = 3 вероятность максимальная. Она составляет: p = 0,321296.
так как при m = 3 вероятность максимальная. Она составляет: p = 0,321296.
|
из
5.00
|
Обсуждение в статье: Мода случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

