Предельные теоремы теории вероятностей

Под предельными теоремами теории вероятностей понимается две группы теорем. К первой группе относятся теоремы, в которых устанавливаются условия, при которых констатируется связь между средним арифметическим большого числа случайных величин и средним арифметическим их математических ожиданий. Эта первая группа теорем носит название закона больших чисел. Таким образом, свойство случайных величин в определённых условиях вести себя практически как не случайные позволяет предсказывать результаты массовых случайных экспериментов с весьма большой долей определённости.

Возможности таких предсказаний, являющихся предметом математической статистики, ещё больше расширяются наличием второй группы теорем, в которых при весьма необременительных ограничениях и условиях устанавливается тот факт, что закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному распределению. Эта группа теорем называется центральной предельной теоремой.

Таким образом, предельные теоремы теории вероятностей являются теоретической предпосылкой математической статистики.

Большой вклад в изучение закона больших чисел внесли российские математики П.Л. Чебышёв, А.Н. Колмогоров, А.Я. Хинчин, Б.В. Гнеденко, В.И. Гливенко. Первую формулировку центральной теоремы дал А.М.Ляпунов.

Лемма Маркова. Если СВ 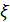принимает только неотрицательные значения и имеет математическое ожидание M( 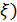, то для любого числа 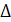имеет место неравенство Маркова:

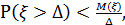(32)

или в равносильной формулировке

(33)

Неравенство Чебышёва. Для любой , имеющей и дисперсию выполняется неравенство Чебышева для любого числа

(34)

Для доказательства заметим равносильность неравенств и , поэтому из формулы (33) для следует:

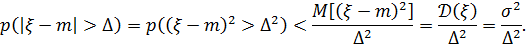
Теорема Чебышёва. Рассмотрим независимые , которые имеют одинаковые математические ожидания и дисперсии

Если теперь увеличивать число , то

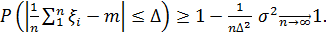(35)

Формулу (35) читают так: среднее арифметическое независимых 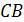, имеющих одинаковые матожидания и дисперсии, сходится по вероятности к матожиданию. Другими словами, среднее арифметическое большого числа независимых 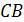, имеющих одинаковые матожидания и дисперсии, с вероятностью, близкой к единице, будет мало отличаться от матожидания.

Неравенство и теорема Бернулли. В схеме повторных испытаний при неограниченном увеличении числа опытов относительная частота появлений события сходится по вероятности к вероятности 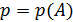появления события в одном опыте:

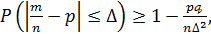(36)

откуда следует,

(37)

Формула (36) называется неравенством Бернулли, а формула (37) составляет содержание теоремы Бернулли.

Наконец, приведём одну из формулировок центральной предельной теоремы:

Если - независимые и имеют одинаковые законы распределения с матожиданием и дисперсией , причём существует третий абсолютный центральный момент , то при неограниченном увеличении 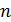закон распределения суммы неограниченно приближается к нормальному.

Мы привели лишь простейшие предельные теоремы теории вероятностей. Они имеют, во-первых, колоссальное теоретическое значение, доказывая наличие закономерностей массовых случайных явлений и возможность их изучения точными математическими методами. В частности, становятся понятными приближённые формулы для формулы Бернулли схемы повторных испытаний, которые ранее принимались без доказательства. Кроме этого, теоремы и неравенства, содержащиеся в них, имеют и практическое значение, поскольку дают крайние оценки вероятностей, справедливые для всех законов распределения.

Пример 43. Оценить «правило трёх сигм», не зная закона распределения.

Требуется вычислить (точнее - оценить) вероятность 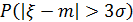. Применим неравенство Чебышева для оценки вероятности :

(38)

Формула (38) показывает, что увеличение диапазона отклонения 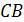от своего матожидания в раз уменьшает вероятность в 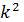раз. В частности, если , то получаем по формуле (38) , тогда как для нормального распределения эта вероятность равна 0,0027, т.е. меньше оценки Чебышёва в 40 раз. Вот что значит дополнительная информация о знании закона распределения!

Пример 44. Количество кормов, расходуемых на ферме крупного рогатого скота в сутки, является случайной величиной, среднее значение которой равно 6т. Оценить вероятность того, что в ближайшие сутки расход кормов на ферме превысит 10т.

Воспользуемся леммой Маркова и формулой : в которой т.е. искомая вероятность менее 0,6.

Пример 45. Подбрасываются 10 игральных костей. Оценить вероятность того, что сумма выпавших очков отклонится от своего матожидания меньше, чем на 10 очков.

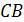
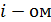Вводим 10 одинаковых число очков при подбрасывании кости),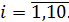

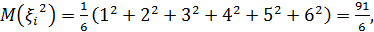следовательно В примере рассматривается .

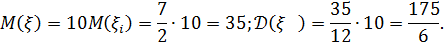
Применяя неравенство Чебышева, получим

0,708.

Пример 46. Путём взятия проб установлено, что потери зерна при уборке составили в среднем 3г. на 1 ; среднее квадратическое отклонение потерь 1г. Определить: 1) вероятность того, что на 1 га потери составят не более 30,1кг; 2) величину, которую не превзойдут потери на 1 га с вероятностью 0,95.

Будем считать, что мы находимся в условиях применяемости центральной предельной теоремы. Действительно, обозначим 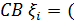потери зерна на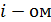 ), 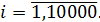Из условия задачи видим, что

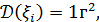
Нас интересует В силу независимости ,

Теперь отвечаем на поставленные вопросы с помощью функции Лапласа для нормального распределения.

1)

2) Исходное равенство: 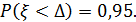Отсюда получаем:

=

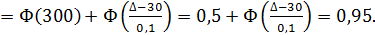
Таким образом, По таблицам функции Лапласа находим тогда , Итак, с вероятностью 0,95 можно утверждать, что потери на 1 га не превзойдут 30,1645 кг.

а) т.е. получили практически достоверное событие.

б) Искомое количество семян обозначим 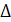. Тогда откуда