Контрольной работы № 1

 

Задача. Найти: а) , ;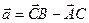

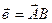б) модуль вектора ;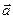

в) скалярное произведение ;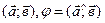

г) векторное произведение векторов ;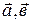

д) смешанное произведение векторов ; .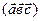

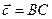Решение:Пусть даны две точки в пространстве А (х₁, у₁, z₁), В (х₂, у₂, z₂). Вектором в пространстве называется направленный отрезок. Обозначается 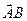, координаты вектора находятся как разность соответствующих координат точек = (х₂ – х₁; у₂ – у₁; z₂ – z₁). Длина вектора находится по формуле 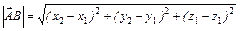. Для двух векторов 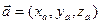, , 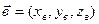, , , 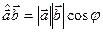j = 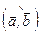, из последней формулы .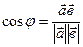

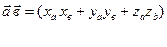Векторное произведение двух векторов вычисляется по формуле 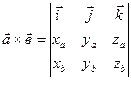, – ортонормированный базис.

Смешанное произведение находится как , где .

Пример. Найти: а) , ;

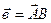б) модуль вектора ;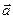

в) скалярное произведение ;

г) векторное произведение векторов ;

д ) смешанное произведение векторов ; .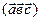

А (4, 2, 6), В (–1, 2, 1), С (1, 0, –1).

 

Решение:

а)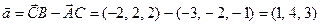

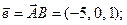
б) ;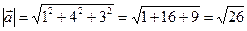

в)

;

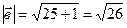
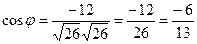г) ;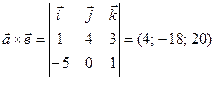

д) ,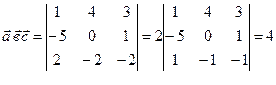

где .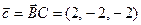

Задача.Доказать, что векторы образуют базис, и найти координаты вектора в этом базисе.

Решение:Базисом в пространстве R_n называется совокупность n векторов, таких, что любой другой вектор этого пространства может быть представлен в виде разложения по данному базису. В трехмерном пространстве R₃ , если существуют числа a, b, g, такие, что любой другой вектор может быть представлен в виде линейной комбинации трех базисных векторов , т. е. 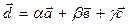. В трехмерном пространстве базисом могут быть любые три некомпланарных вектора, так как их смешанное произведение не равно нулю: .

 

Пример. Доказать, что векторы образуют базис, и найти координаты вектора в этом базисе: , , .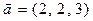

 

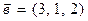
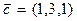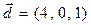Решение: образуют базис, если они некомпланарные, т. е.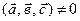

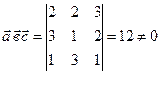, так как смешанное произведение отлично от нуля, то образуют базис. В данном базисе любой другой вектор представлен в виде линейной комбинации данных векторов 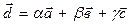, a, b, g – координаты вектора в базисе .

Последнее равенство равносильно системе:

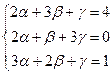, D = 12 ¹ 0, то система имеет единственное решение.

,

,

.

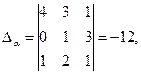
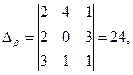
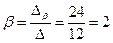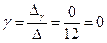Ответ: = .

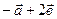Задача.Сила 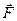приложена к точке А. Вычислить:

а) работу силы 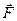, если точка ее приложения, двигаясь прямолинейно, переместилась в точку В;

б) модуль вращающего момента силы 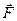, приложенной к точке В.

 

Решение:Если некоторая сила 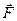приложена к материальной точке А и при этом точка А прямолинейно переместилась в точку В, то работа А силы определяется по формуле А = 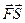, где 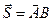. Понятие векторного произведения применяется при решении физических задач. Например, для нахождения вращающего момента силы 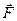пользуемся формулой 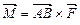, где – сила, приложенная к точке В, относительно точки А.

 

Пример. Сила 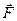приложена к точке А. Вычислить:

а) работу силы 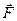, если точка ее приложения, двигаясь прямолинейно, переместилась в точку В;

б) модуль вращающего момента силы 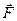относительно точки В.

 

Решение:

а)ИзвестноА = 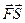, 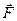= (3, 2, –1), А (1, 3, 1), В (3, 5, 0), где 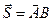, так как точка А переместилась в точку В, то 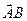= (2, 2, –1); следовательно, А = (3, 2, –1)(2, 2, –1) = 6 + 4 + 1 = 11.

Ответ: А = 11;

б) 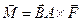, 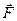= (3, 2, –1),

.

.

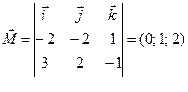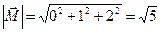Ответ: .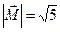

Задача.Заданы три точки пространства А, В и С. Найти:

а) уравнение стороны АВ треугольника АВС;

б) периметр треугольника (до 0,01);

в) уравнение плоскости (АВС);

г) площадь треугольника (до 0,01).

 

Решение:Уравнение прямой, проходящей через две точки пространства А (х₁, у₁, z₁) и В (х₂, у₂, z₂), имеет вид

(АВ): .

Уравнение плоскости, проходящей через три точки пространства, имеет вид

(АВС): 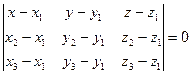, где С (х₃, у₃, z₃) некоторая точка пространства, отличная от А и В. Площадь треугольника, построенного на двух векторах, находится по формуле S= .

 

Пример. Заданы три точки пространства А, В и С (координаты точек взять из задания 1.1. Найти:

а) уравнение стороны АВ треугольника АВС;

б) периметр треугольника (до 0,01);

в) уравнение плоскости (АВС);

г) площадь треугольника (до 0,01).

А (4, 2, 0), В (–1, 2, 1), С (1, 0, –1).

 

Решение:

а) Уравнение прямой, проходящей через две точки А (4, 2, 0) и В (–1, 2, 1), имеет вид (АВ):

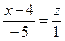и у = 2;

б)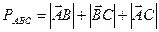

;

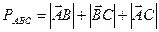
в) (АВС):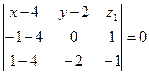

2(х – 4) – 8(у – 2) + 10z = 0

2х – 8у + 10z + 8 = 0

х – 4у + 5z + 4 = 0.

Ответ: х – 4у + 5z + 4 = 0;

г)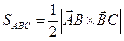

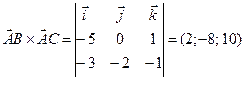
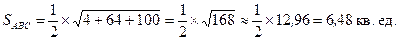
Ответ: S = 6,48 кв. ед.

Задача.Проверить совместность системы линейных алгебраических уравнений и решить ее:

а) методом Крамера;

б) методом Гаусса;

в) матричным методом.

 

Решение:Система n линейных алгебраических уравнений с n неизвестными имеет единственное решение, если определитель, составленный из коэффициентов, при неизвестных отличен от нуля.

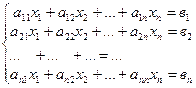(1)

 

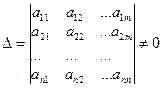
Рассмотрим три метода решения систем линейных алгебраических уравнений:

а) Правило Крамера (m = n)

Система (1) имеет единственное решение, если D ¹ 0, которое находится из формулы

х_i = ,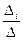

где D_I – определитель, полученный из определителя D путем замены i-того столбца столбцом свободных членов системы.

б) Метод Гаусса

Система m линейных алгебраических уравнений с m неизвестными с помощью элементарных преобразований приводится к виду:

 

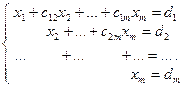(2)

 

Из последнего уравнения определяется х_m , из предпоследнего уравнения находится х_m–1 и т. д.

в) Матричный метод

Систему (1) можно записать в виде

 

АХ = В, (3)

где А = 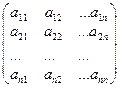– квадратная матрица, причем detA ¹ 0.

Х = 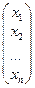, В = .

Умножив обе части равенства (3) на А^–1, получим

А^–1АХ = А^–1В или Х = А^–1В. (4)

А^–1 – обратная матрица.

 

А^–1= 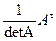, А^t= , (5)

 

А_ij – алгебраические дополнения к соответствующим элементам а_ij. А_ij = (–1)^i+jM_ij . M_ij – минор элемента а_ij. Минор M_ij – это определитель (n – 1)-го порядка, полученный из определителя D n-го порядка путем вычеркивания i-той строки и j-того столбца.

Задача. Проверить совместность системы линейных алгебраических уравнений и решить ее: а) методом Крамера, б) методом Гаусса, в) матричным методом.

Решение: Система n линейных алгебраических уравнений с n неизвестными имеет единственное решение, если определитель, составленный из коэффициентов, при неизвестных отличен от нуля

.

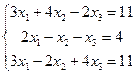а) Метод Крамера

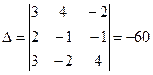
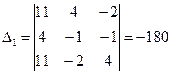, х₁ =

, х₂ =

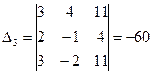, х₃ = .

Ответ: (3, 1, 1).

 

б) Метод Гаусса

Выпишем расширенную матрицу системы и преобразуем ее

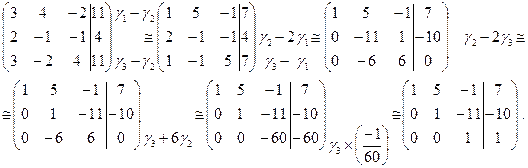
Последней матрице соответствует система уравнений, эквивалентная исходной.

.

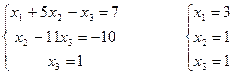Ответ: (3, 1, 1).

 

в) Матричный метод

Систему (1) можно записать в виде

АХ = В,

тогда Х = А^–1В det = –60

X = –

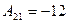
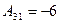
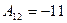
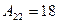
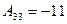
Х= = .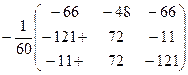

 

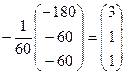Ответ: (3, 1, 1).

1.2. Методические указания и решение типового варианта