Циркуляция и вихрь векторного поля

Рассмотрим в поле 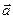линию L и выберем на ней направление. Для произвольной точки М кривой запишем радиус-вектор 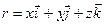, вектор 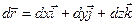будет направлен по касательной к кривой в направлении ее обхода .

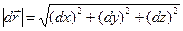Определение: Циркуляцией вектора 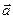вдоль кривой L называется криволинейный интеграл по замкнутому контуру L от скалярного произведения вектор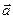а на 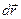(касательный к L)

,

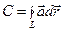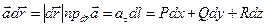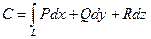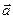или, учитывая, что , получим , где – проекция вектора на касательную 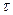, проведенную в направлении обхода.

Физический смысл циркуляции состоит в том, что если кривая L расположена в силовом поле, то циркуляция – это работа силы 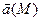поля при перемещении материальной точки вдоль L.

Замечание.Циркуляция отлична от нуля вдоль замкнутой линии, так как в каждой точке векторной линии 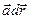сохраняет значение: положительное, если направление 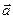совпадает с направлением обхода линии; отрицательное – в противоположном случае.

Определение: Вихревым вектором или ротором векторного поля 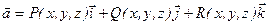называется вектор, определяемый равенством .

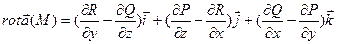Или .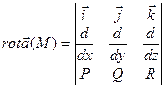

Свойства ротора:

1) 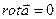, если 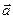– постоянный вектор,

2) 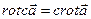, где с = const,

3) ,

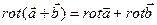4) 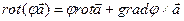, где 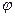– скалярная функция.

Формула Стокса примет вид:

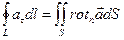– это векторная форма формулы, которая показывает, что циркуляция вектора 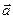вдоль замкнутого контура L равна потоку ротора этого вектора 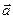через поверхность S, лежащую в поле вектора 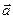и ограниченную контуром L.

Так как по теореме о среднем, то .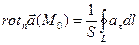

Если контур L стягивается в точку М, то 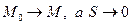и .

Замечание. Направление ротора – это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S. Поэтому связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению.

Оператор Гамильтона

Определение:Векторными операциями первого порядка называется взятие градиента, дивергенции и ротора.

Оператор Гамильтона (символический вектор) имеет вид:

.

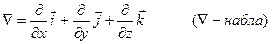С помощью оператора Гамильтона основные дифференциальные операции можно записать так:

,

,

,

,

.

 

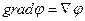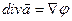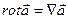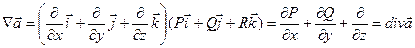Задача. Вычислить координаты центра масс однородного тела, ограниченного поверхностями: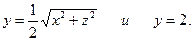

 

Решение:Данное тело симметрично относительно оси ОY, поэтому x_c = z_c = 0 (т. е. центр симметрии находится на оси ОY). Ордината центра масс найдется по формуле:

.

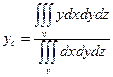Перейдем к цилиндрическим координатам: 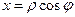, , , 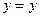тогда

1) 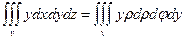. Для нахождения пределов интегрирования найдем проекцию области на плоскость OXZ, получим 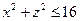, следовательно, 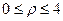, , 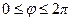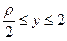. Получим кратный интеграл

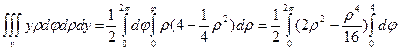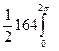= = 16p;

 

2) = = ;

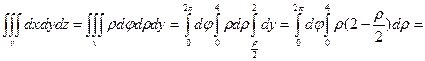
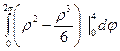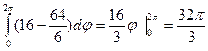3) .

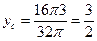Итак, центр масс С (0; ; 0).

Задача. Вычислить производную функции Z = arctg(хy) в точке М₀ (1,1) вдоль кривой у = х², в положительном направлении оси ОХ.

Решение: Если функция u = f (x, y, z) определена в окрестности точки М (х₀, у₀, z₀), то производная функции по направлению вектора 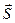определяется по формуле:

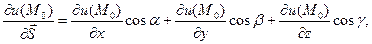
где 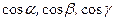– направляющие косинусы вектора .

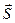Производной вдоль кривой L называют производную по направлению ориентированной касательной к кривой, вычисленную в точке касания.

За направление параболы у = х² в точке М₀ (1,1) возьмем направление касательной к параболе в этой точке, задаваемой углом a, который касательная образует с осью ОХ. Тогда

 

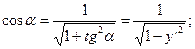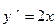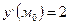так как и , то

; .

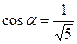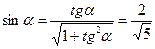Найдем частные производные функции, U = arctg (xy), в точке М (1,1):

; .

 

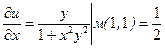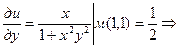
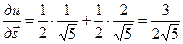Поверхностный интеграл первого рода определяется равенством

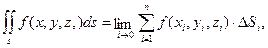при условии существования предела, где S_i – элемент поверхности S¢, ÆS_i – диаметр частичных поверхностей, 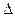S_i – площади частичных поверхностей. Для вычисления поверхностного интеграла применим формулу: где D – проекция поверхности S на плоскости ОХУ является однозначной, тогда F(x, y) = Z – уравнение поверхности.

Задача. Вычислить 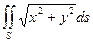, где S – часть конической поверхности х² + у² = z², расположенной между плоскостями Z = 0 и Z = 2.

 

Решение: Из уравнения поверхности находим 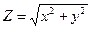, при 0 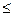Z 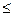2; проекцией этой поверхности на плоскость ОХY является круг х² + у² 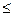4.

;

 

 

.

 

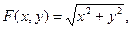
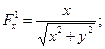
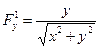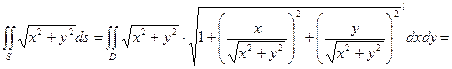
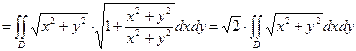Перейдем к полярным координатам 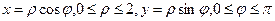, получим:

.

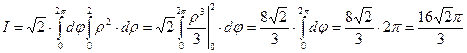Если S – гладкая замкнутая поверхность, ограничивающая V и Р = Р (х, у, z), Q = Q (x, y, z), R = R (x, y, z) – непрерывные функции вместе со своими частными производными первого порядка, то имеет место формула Остроградского – Гаусса:

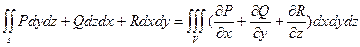
или

(*)

Задача. Вычислить: , если S – поверхность, ограниченная плоскостями x = 0, y = 0, z = 0, x + 2y + 3z = 6.

По формуле Остроградского – Гаусса имеем: 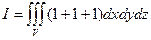, так как P(x, y, z) = x + y и 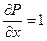, Q (x, y, z) = y + z и 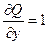, R(x, y, z)=z+x и 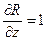, следовательно, 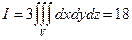, геометрически последний интеграл выражает объем области V (тетраэдра), ограниченный координатными плоскостями и плоскостью х + 2у + 3z = 6, или в отрезках уравнение плоскости имеет вид: .

 

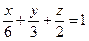Задача. Вычислить поток векторного поля 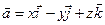через верхнюю часть плоскости х + 2у + 3z – 6 = 0, расположенной в первом октанте.

 

Решение: Выразим Z из уравнения плоскости: 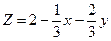, тогда .

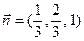Вычислим поток, пользуясь формулой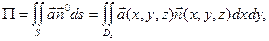

=

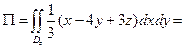
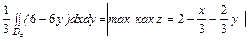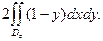
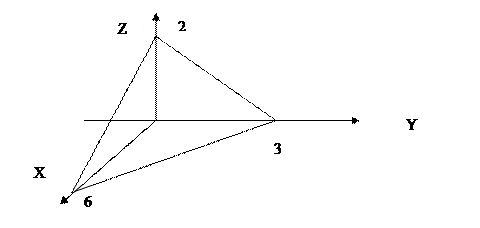
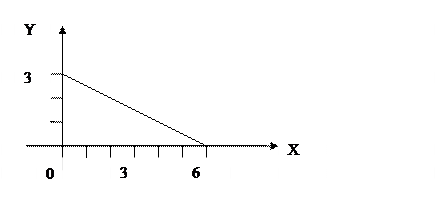
Так как проекцией плоскости х + 2у + 3z – 6 = 0 на плоскости ОХY является треугольник, ограниченный прямыми у = 0, х = 0 и х + 2у = 6, то 0 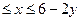(см. рисунок), то

 

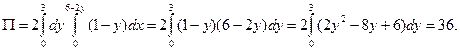
Задача. Вычислить дивергенцию векторного поля

 

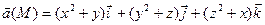в точке М₀(1, –2, 3).

 

Решение:

 

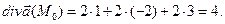
Так как 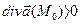, то точка М₀ является источником поля.

 

Вопросы для контроля

 

1. Первообразная. Теорема о первообразных.

2. Свойства неопределенных интегралов. Таблица интегралов.

3. Методы интегрирования (по частям, замена переменной).

4. Интегрирование дробно-рациональных функций.

5. Интегрирование простейших дробей.

6. Интегрирование тригонометрических выражений.

7. Интегрирование иррациональных функций.

8. Вычисление площадей плоских фигур с помощью определенного интеграла.

9. Свойства определенного интеграла. Формула Ньютона – Лейбница.

10. Интегрирование по частям и замена переменной в определенном интеграле.

11. Несобственный интеграл.

12. Числовые ряды. Свойства рядов. Кратные интегралы.

13. Геометрический и гармонический ряды. Необходимый признак сходимости.

14. Признаки сходимости положительных рядов.

15. Степенной ряд. Область сходимости и радиус сходимости.

16. Теорема Абеля.

17. Ряды Фурье.

18. Дифференциальные уравнения. Дифференциальные уравнения первого порядка: однородные, с разделяющимися переменными, линейные.

19. Уравнение Бернулли и методы его решения.

20. Дифференциальные уравнения второго порядка, допускающие понижение.

21. Дифференциальные уравнения второго порядка с постоянными коэффициентами.

22. Дифференциальные уравнения однородные и неоднородные.

23. Частное решение дифференциального уравнения.

24. Дифференциальные уравнения высших порядков.

25. Системы дифференциальных уравнений. Приближенное решение дифференциального уравнения.

26. Элементы теории поля. Поверхности и линии уровня.

27. Производная по направлению. Градиент скалярного поля и его свойства.

28. Векторное поле.

29. Поток векторного поля.

30. Дивергенция.

31. Ротор.