 |
Главная |
Формула Симпсона (формула парабол) (n–четное)
|
из
5.00
|
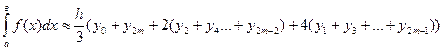 , где
, где 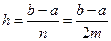 .
.
Остаточный член имеет вид 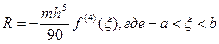 .
.
Задача. Вычислить интеграл 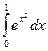 по формуле Симпсона при n = 10 и оценить остаточный член.
по формуле Симпсона при n = 10 и оценить остаточный член.
Решение: Оценим остаточный член.
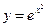 ,
, 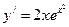 ,
, 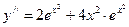 ,
, 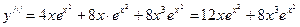 ,
,
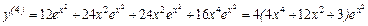 .
.
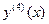 имеет наибольшее значение на
имеет наибольшее значение на 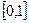 при х = 1, m = 5,
при х = 1, m = 5, 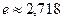
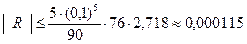 .
.
Составим таблицу значений, запишем ординаты с четными и нечетными номерами в разные столбцы:
| i | xi | xi2 | yi, i=0, 10 | y2m | y2m–1 |
| 0,0 | 0,00 | 1,000 | 1,0101 | ||
| 0,1 | 0,01 | ||||
| 0,2 | 0,04 | 1,0407 | 1,0942 | ||
| 0,3 | 0,09 | ||||
| 0,4 | 0,16 | 1,1735 | 1,2840 | ||
| 0,5 | 0,25 | ||||
| 0,6 | 0,36 | 1,4333 | 1,6323 | ||
| 0,7 | 0,49 | ||||
| 0,8 | 0,64 | 1,8965 | |||
| 0,9 | 0,81 | 2,2479 | |||
| 1,0 | 1,0 | 2,7188 |
Суммы: у0 + у10 = 3,7188,
åу2m = 5,44,
åу2m–1 = 7,2685.
По формуле Симпсона получаем: 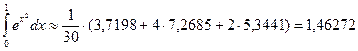 ; округляем до четырех знаков, окончательно получим
; округляем до четырех знаков, окончательно получим 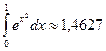 .
.
Задача.Решить систему дифференциальных уравнений с помощью составления характеристического уравнения
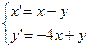 .
.
Решение: Фундаментальную систему решений будем отыскивать в виде 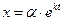 ;
; 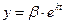 , тогда
, тогда 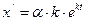 ,
, 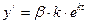 . Подставим полученные значения в систему уравнений:
. Подставим полученные значения в систему уравнений:
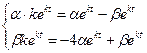
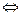
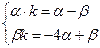
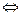
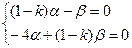 .
.
Составим характеристическое уравнение 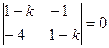 или
или
(1 – к)2 – 4 = 0 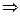 1 – к = ±2, откуда 1 – к = –2, к = 3 или 1 – к = 2, к = –1.
1 – к = ±2, откуда 1 – к = –2, к = 3 или 1 – к = 2, к = –1.
При к = –1 получим систему уравнений 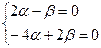
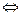
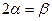 . Пусть
. Пусть 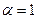
 , тогда
, тогда 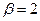 , откуда
, откуда 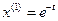 ,
, 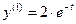 – фундаментальная система решений.
– фундаментальная система решений.
При к = 3 получим систему уравнений: 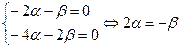 . Пусть
. Пусть 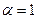
 , тогда
, тогда 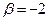 , откуда
, откуда 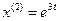 ,
, 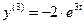 .
. 
Общее решение системы уравнений запишется в виде:
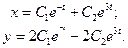
Задача. Разложить в степенной ряд по степеням x решение дифференциального уравнения 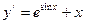 , записать первые три, отличных от нуля, члена разложения.
, записать первые три, отличных от нуля, члена разложения.
Решение: 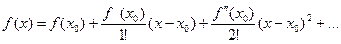 .
.
Продифференцируем исходное уравнение не менее двух раз.
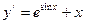 ,
,
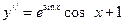 ,
,
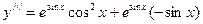 .
.
Имеем: 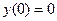 ,
, 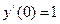 ,
, 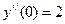 ,
, 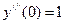 , подставим полученные значения в степенной ряд:
, подставим полученные значения в степенной ряд: 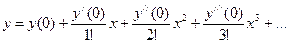 , получим приближенное решение дифференциального уравнения
, получим приближенное решение дифференциального уравнения 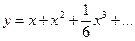 .
.
Задача. Записать уравнение кривой, проходящей через точку P (1,2), для которой площадь треугольника, образованного радиус-вектором любой точки кривой касательной в этой точке и осью абсцисс, равна 2.
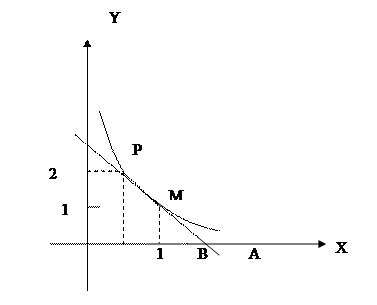
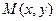 – произвольная точка кривой. ОМ – радиус-вектор. МА – касательная к кривой. Известно, что
– произвольная точка кривой. ОМ – радиус-вектор. МА – касательная к кривой. Известно, что 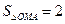 . Найти уравнение кривой.
. Найти уравнение кривой.
Решение:
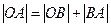 , так как
, так как 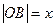 , то
, то 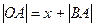 . Из
. Из 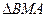 имеем:
имеем: 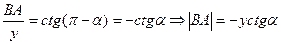 или
или 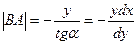 , тогда
, тогда 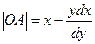 . Площадь треугольника ОМА равна
. Площадь треугольника ОМА равна 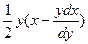 , и, так как по условию задачи
, и, так как по условию задачи 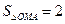 , получим уравнение
, получим уравнение  . Решим это уравнение, выполнив некоторые преобразования
. Решим это уравнение, выполнив некоторые преобразования 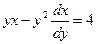 ,
, 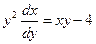 ,
, 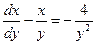 , последнее уравнение – линейное, первого порядка относительно
, последнее уравнение – линейное, первого порядка относительно 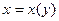 , поэтому используем подстановку
, поэтому используем подстановку 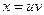 ;
; 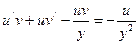 ;
; 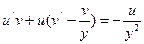 ;
; 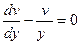 ;
; 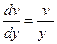 ;
; 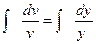 ;
; 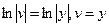 ,
, 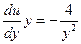 ;
; 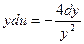 ;
; 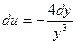 ;
; 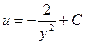 .
.
Итак, 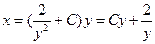 .
.
По условию задачи кривая проходит через точку Р (1, 2), поэтому С = 0, так как 1 = 2С + 1; следовательно, искомая кривая имеет вид 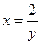 или xy = 2 – гипербола.
или xy = 2 – гипербола.
2.2. Методические указания и решение типового варианта
Контрольной работы № 4
Элементы теории поля
Основными понятиями являются: градиент, поток, потенциал, дивергенция, ротор, циркуляция.
Определение: Полем называется область некоторого пространства, в каждой точке которой определено значение некоторой величины.
Определение:Если каждой точке М области V соответствует определенное число j = j(М), то говорят, что в области V задано скалярное поле.
Определение:Если каждой точке М из области V соответствует некоторый вектор 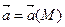 , то говорят, что задано векторное поле.
, то говорят, что задано векторное поле.
Если функция j(М) ( 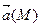 ) не зависит от времени, то скалярное (векторное) поле называется стационарным, а поле, которое меняется с течением времени, называется нестационарным.
) не зависит от времени, то скалярное (векторное) поле называется стационарным, а поле, которое меняется с течением времени, называется нестационарным.
В трехмерном пространстве каждой точке М области можно поставить в соответствие либо ее координаты (х, y, z), либо радиус-вектор 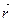 . Следовательно, скалярное поле j можно задать как функцию трех переменных j (х, y, z) или как функцию одной переменной j (
. Следовательно, скалярное поле j можно задать как функцию трех переменных j (х, y, z) или как функцию одной переменной j ( 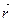 ).
).
Определение: Множество точек поля, в которых скаляр j имеет одно и то же значение, называется поверхностью уровня поля j (х, y, z) = С, где C = const.
Так как функция поля однозначна, то через каждую точку поля М (х1, y1, z1) проходит единственная поверхность уровня j (х, y, z) = j( х1, y1, z1).
Пусть М – произвольная точка пространства, где задано поле j = j(х, y, z). Производной функции j в точке М в направлении любого вектора 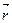 называется предел отношения приращения Dj = j(М1) – j(М) к Dr, при Dr®0 (М1®М), т. е.
называется предел отношения приращения Dj = j(М1) – j(М) к Dr, при Dr®0 (М1®М), т. е.
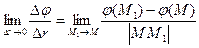 , обозначают
, обозначают 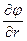 .
.
Производная характеризует скорость изменения функции (поля) в заданной точке М в направлении вектора 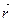 .
.
Если 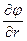 > 0, то функция j возрастает в направлении вектора
> 0, то функция j возрастает в направлении вектора 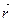 , если
, если 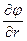 < 0, то функция j убывает в направлении вектора
< 0, то функция j убывает в направлении вектора 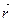 .
.
½ 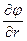 ½ – есть мгновенная скорость функции j в направлении вектора
½ – есть мгновенная скорость функции j в направлении вектора 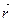 .
.
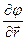 =
= 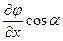 +
+ 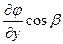 +
+ 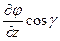 , где
, где 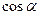 ,
, 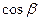 ,
, 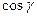 – направляющие косинусы вектора
– направляющие косинусы вектора 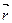 .
.
Определение: Градиентом функции j (х, y, z) обозначают gradj , называют вектор, координатами которого являются значения частных производных функции j (х, y, z) в точке М (х, y, z):
gradj = 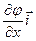 +
+ 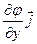 +
+ 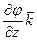 , где
, где 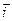 ,
, 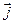 ,
, 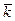 – единичные векторы, или gradj=(
– единичные векторы, или gradj=( 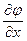 ;
; 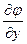 ;
; 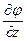 ).
).
Направление градиента совпадает с направлением наибыстрейшего роста функции (поля), следовательно, наибольшая скорость изменения поля j в точке М равна
êgradjê= 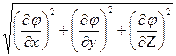 .
.
Перечислим свойства градиента.
Теорема:Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
1) grad(u + v) = gradu + gradv,
2) grad(cu) = cgradu, c = const,
3) grad(uv) = u gradv + v gradu,
4) grad 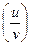 =
= 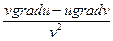 ,
,
5) gradF(u) = 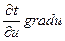 .
.
Векторное поле
Определение: Векторной линией поля 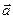 называется линия, касательная к которой в каждой ее точке М имеет направление соответствующего ей вектора поля. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
называется линия, касательная к которой в каждой ее точке М имеет направление соответствующего ей вектора поля. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Векторная линия 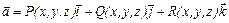 описывается системой
описывается системой
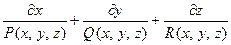 .
.
Пусть векторное поле образовано вектором 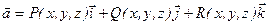 . К понятию векторного поля приводит физическая задача, изучающая поля скоростей текущей жидкости. Некоторая поверхность z находится в этом потоке и пропускает жидкость. Найдем количество жидкости, протекающей через поверхность z. Разобьем эту поверхность на n частичных областей произвольным образом S1, S2, ... ,Sn и выберем в каждой части области некоторую точку Мi, в которой построим единичный вектор нормали
. К понятию векторного поля приводит физическая задача, изучающая поля скоростей текущей жидкости. Некоторая поверхность z находится в этом потоке и пропускает жидкость. Найдем количество жидкости, протекающей через поверхность z. Разобьем эту поверхность на n частичных областей произвольным образом S1, S2, ... ,Sn и выберем в каждой части области некоторую точку Мi, в которой построим единичный вектор нормали 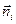 . За единицу времени через Si протекает количество жидкости, приближенно равное
. За единицу времени через Si протекает количество жидкости, приближенно равное 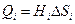 , где
, где 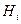 – высота i-того цилиндра, а
– высота i-того цилиндра, а 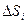 – площадь i-той площади. Но
– площадь i-той площади. Но 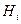 является проекцией вектора
является проекцией вектора 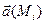 на нормаль
на нормаль 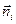 :
: 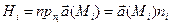 , следовательно, общий объем жидкости, протекающий через поверхность S за единицу времени, равен приближенно:
, следовательно, общий объем жидкости, протекающий через поверхность S за единицу времени, равен приближенно: 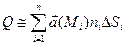 . Точное значение этой величины получим, перейдя к пределу при неограниченном увеличении числа частичных площадок. Если
. Точное значение этой величины получим, перейдя к пределу при неограниченном увеличении числа частичных площадок. Если 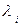 – диаметр площади, то
– диаметр площади, то
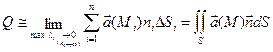 .
.
Определение: Предел суммы элементарных потоков через частичные области, на которые разбивается область S, когда число частичных областей неограниченно растет при условии, что наибольший из диаметров площади неограниченно убывает, называется потоком векторного поля 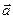 через поверхность S.
через поверхность S.
Определение: Потоком вектора 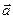 через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности
через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности
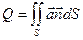 или
или 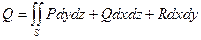 .
.
Замечание.Поток вектора 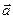 есть величина скалярная, равная объему жидкости, протекающей через поверхность S за единицу времени.
есть величина скалярная, равная объему жидкости, протекающей через поверхность S за единицу времени.
Если поверхность замкнута и ограничивает некоторый объем, то 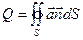 , в этом случае за направление вектора
, в этом случае за направление вектора 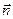 берут направление внешней нормали и говорят о потоке изнутри. Так как
берут направление внешней нормали и говорят о потоке изнутри. Так как 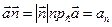 , то
, то 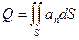 .
.
|
из
5.00
|
Обсуждение в статье: Формула Симпсона (формула парабол) (n–четное) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

