Формула Ньютона для интерполирования вперед и экстраполирования назад

Пусть точка интерполирования х находится ближе к левому концу отрезка [a,b] или слева от него. Тогда интерполяционная формула Ньютона для интерполирования вперед и экстраполирования назад примет вид

,

где 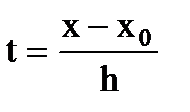- новая переменная, - конечная разность k - го порядка.

Связь разностных соотношений и конечных разностей:

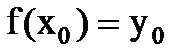, , и т.д.

Остаток в этом случае имеет вид

.

Формула Ньютона для интерполирования назад и экстраполирования вперед

Пусть точка интерполирования х находится ближе к правому концу отрезка [a,b] или справа от него. За первый узел интерполирования примем ближайший и обозначим его через х_k. Тогда интерполяционная формула Ньютона для интерполирования назад и экстраполирования вперед примет вид

,

где - новая переменная.

Связь разностных соотношений и конечных разностей:

, , и т.д.

Остаток в этом случае имеет вид

.

Правило определения максимального порядка разностей, которые ведут себя правильно:

если , а , то максимальный порядок разностей, которые ведут себя правильно, равен j. Использование разности порядка (j+1) приведет к искажению результата. Здесь e - абсолютная погрешность вычисленных значений у_i.

Интерполяционные формулы Гаусса.

Пусть узлы интерполирования х₀, х₁, ..., х_n равноотстоящие и точка интерполирования х находится в середине отрезка [a,b] "вблизи" узла х_k, причем х>x_k. Для построения интерполяционной формулы необходимо привлекать узлы интерполирования в следующем порядке: х_k, x_k+h, x_k-h, ..., x_k+ih, x_k-ih. Обозначив и вводя конечные разности по формулам:

, , и т.д.,

то для интерполирования вперед формула Гаусса примет вид

Если точка интерполирования х<х_k, то узлы для построения следует привлекать в следующем порядке: х_k, x_k-h, x_k+h, ..., x_k-ih, x_k+ih.

Формула Гаусса для интерполирования назад имеет вид

Построение кривой по точкам

Общие понятия

В инженерной практике часто используют совокупности точек, абсциссы которых различны, полученные в результате экспериментов. Назначение численных методов заключается в определении зависимости, которая связывает данный набор точек. Другими словами в этом случае численные методы определяют класс допустимых формул, коэффициенты которых должны быть определены. Существует множество различных типов функций, которыми можно воспользоваться. Рассмотрим класс линейных функций вида: . Все рассмотренные до этого методы позволяли получить полиномы, достаточно хорошо аппроксимирующие или интерполирующие данные при условии, что эти данные достаточно точны, т.е. точки получены, по крайней мере, с пятью знаками точности. Однако, часто в измерениях экспериментальная ошибка достаточно велика, т.е. истинное значение удовлетворяет равенству: , где 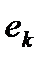- ошибка измерения.

Для того, чтобы определить насколько далеко от данных лежит кривая можно воспользоваться следующими нормами:

- максимальная ошибка, (4.1)

- средняя ошибка, (4.2)

- среднеквадратичная

ошибка. (4.3)

Пример:Сравним ошибки для линейного приближения функции по заданной таблице точек

Решение:

Вычислим все три вида ошибок:

.

.

.

Таким образом, построенная наилучшим образом линия определяется минимизацией одной из величин, заданных выражениями (4.1) – (4.2). В связи с тем, что третью норму легче минимизировать выбирают её.