Кинематические уравнения (в кватернионной форме)

Рассмотрим поворот подвижной системы координат СКm относительно неподвижной – СКs. Ориентацию подвижной системы координат относительно неподвижной зададим кватернионом .

Зададим в системе координат СКs вектор 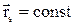. Тогда

. (1.48)

Продифференцируем выражение (1.58)

. (1.49)

Учтем

и . (1.50)

Т.к. ; то . (1.51)

Тогда

. (1.52)

Следовательно, выражение (1.49) примет вид

. (1.53)

Пусть

(1.54)

Покажем, что

. (1.55)

Действительно:

(1.56)

Сравнивая формулы (1.53) и (1.55), можем записать выражение для угловой скорости поворота системы координат СКm относительно неподвижной системы СКs, выраженное в проекциях на оси системы координат СКm.

. (1.57)

Тогда кинематические уравнения принимают вид:

(1.58)

В развернутом виде уравнение (1.58) имеем вид:

(1.59)

 

Или в матричной форме записи

(1.60)

Здесь

; (1.61)

 

1.6. Контрольные вопросы

1. Что такое "углы ортогонального поворота"?

2. Сколько имеет место вариантов задания угловой ориентации твердого тела?

3. Дайте определение угла курса ЛА.

4. Дайте определение угла тангажа ЛА.

5. Дайте определение матрицы направляющих косинусов по Литвин-Седому, определяющей ориентацию связанной системы координат относительно географической.

6. В чем проявляется свойство ортогональности матрицы направляющих косинусов?

7. Постройте матрицу направляющих косинусов, определяющей ориентацию связанной системы координат относительно географической.

8. Как определить угловую скорость системы координат относительно неподвижной при известной матрице направляющих косинусов, определяющей ее ориентацию?

9. Нарисуйте кинематическую схему связей между используемыми системами координат для задания ориентации ЛА.

10. Составьте граф-схему ортогональных поворотов для связи систем координат, заданных в п.9.

11. Дать определение кватерниону и записать его в разных возможных формах записи.

12. Запишите кинематическое уравнение (уравнение Пуассона) через матрицы направляющих косинусов.

13. Запишите кинематическое уравнение (уравнение Пуассона) через кватернионы в матричной форме.

 

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ОРИЕНТАЦИИ ЛА ПО ПОКАЗАНИЯМ ГИУ

 

 

Постановка задачи.

 

На борту летательного аппарата установлено n гироскопических измерительных устройств (ГИУ), позволяющих определять/измерять угловые перемещения летательного аппарата. ГИУ установлены на борту ЛА с разной ориентацией своих осей подвеса (см. Рис.2.1.). Таким образом каждый из ГИУ может измерить разные параметры ориентации ЛА Г_i (обычно два параметра) из рассматриваемого набора параметров ориентации ЛА Г. По результатам измерений ГИУ Г_gi , поступающих на блок обработки сигналов (БОС), в последнем по заданным алгоритмам определяются/вычисляются оценки

параметров ориентации ЛА Г^о.

 

Рис.2.1.

 

Связь между системами координат, используемых при решении задач определения ориентации ЛА, определим схемой (см. рис.2.2).

Рис.2.2. Связь между системами координат

Здесь использованы следующие системы координат:

X₀Y₀Z₀ – инерциальная система координат;

X_gY_gZ_g – географическая система координат;

X_vY_vZ_v – путевая система координат;

X_cY_cZ_c – связанная система координат;

X_ujY_ujZ_uj – установочная система координат j-ого измерительного устройства;

Y_j – ось, совпадающая с главной осью гироскопического измерительного устройства.

Введем схему ГИУ (см. Рис.2.2.), в которой зададим направления основных осей (осей подвеса гироузла) относительно установочной системы координат и положительные направления углов поворота гироузла ГИУ.

Рисунок соответствует положению гироузла при углах α_i = 0, β_i =0.

Матрицы ориентации систем координат заданы в виде:

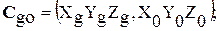
(2.1)

 

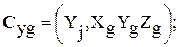
Рис.2.3. ГИУ (α_j=0_, β_j=0).

 

 

Здесь

; (2.2)

 

; (2.3)

 

. (2.4)

Случай 1. Вектор кинетического момента j-ого ГИУ неподвижен в географической системе координат, что имеет место при идеальной работе, например, гировертикали или гирополукомпаса.

Т.е. матрицы .

Тогда для j-ого ГИУ согласно кинематической схеме (см. рис.2.2) имеет место соотношение

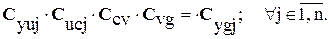
Или (2.5)

Зададим начальные условия в виде:

. (2.6)

Тогда параметры матрицы , определяющей ориентацию вектора кинетического момента ГИУ, находится из выражения:

(2.7)

Параметры ориентации ЛА можно определить по показаниям ГИУ на основании уравнения (2.5)

Это уравнение распадается на три скалярных уравнения, которое в общем виде запишем как

(2.8)

(2.9)

(2.10)

 

Из уравнения (2.8) находится информация, которая имеется в измеренном ГИУ-ом угле , а из уравнений (2.9) и (2.10) - находится информация, которая имеется в измеренном ГИУ-ом угле 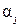. Располагая n ГИУ на борту ЛА и располагая их соответствующим образом, можно получить полную информацию об угловой ориентации ЛА.

Случай 2. Пусть вектор кинетического момента ГИУ неподвижен относительно геоцентрической инерциальной системы координат, что имеет место при идеальной работе, например, определенных видов гироплатформ, неподвижных в инерциальном пространстве. Т.е. матрицы .

Аналогично выше рассмотренному, составим для каждого ГИУ согласно кинематической схеме (см. рис.2.3) соотношения. Тогда для j-ого ГИУ согласно кинематической схеме (см. рис.2.2) имеем

Или (2.11)

Зададим начальные условия в виде:

. (2.12)

Тогда параметры матрицы , определяющей ориентацию вектора кинетического момента ГИУ, находится из выражения:

(2.13)

Параметры ориентации ЛА можно определить по показаниям ГИУ на основании уравнения (2.11)

Это уравнение распадается на три скалярных уравнения, которое в общем виде запишем как

(2.14)

(2.15)

( 2.16)

Из уравнения (2.14) находится информация, которая имеется в измеренном ГИУ-ом угле , а из уравнений (2.15) и (2.16) - находится информация, которая имеется в измеренном ГИУ-ом угле 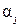. Располагая n ГИУ на борту ЛА и располагая их соответствующим образом, можно получить полную информацию об угловой ориентации ЛА.

Уравнения (2.11) позволяют получить кинематические уравнения связи между искомыми параметрами ориентации, что и позволяет построить алгоритм работы БОС (см. рис.2.1.) для оценки параметров ориентации ЛА.